算法学习之gumbel softmax

1. gumbel_softmax有什么用呢?

假设如下场景:
模型训练过程中, 网络的输出为p = [0.1, 0.7, 0.2], 三个数值分别为"向左", “向上”, "向右"的概率。 我们的决策可能是y = argmax§, 也即选择"向上"这条决策。
但是，这样做会有两个问题:

1. argmax()函数是不可导的。这样网络就无法通过反向传播进行学习。
2. argmax()的选择不具有随机性。同样的输出p选择100次,每次的结果都为"向上"。而按照概率为0.7的含义,100次应该有70次左右的决策结果是选择"向上".

而gumbel_softmax的作用就是解决上述这两个子问题.。

2.argmax(x)是什么?为什么不可导?

为了更直观,这里使用两维的vector
y = argmax(x); x = (x1, x2)

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.patches import FancyArrowPatch

# https://www.itdaan.com/blog/2014/04/04/32dfc1abfd5a635469b7762c516a37b3.html
class Arrow3D(FancyArrowPatch):
    def __init__(self, xs, ys, zs, *args, **kwargs):
        FancyArrowPatchcyArrowPatch.__init__(self, (0, 0), (0, 0), *args, **kwargs)
        self._verts3d = xs, ys, zs
    def draw(self, renderer):
        xs3d, ys3d, zs3d = self._verts3d
        xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
        self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
        FancyArrowPatch.draw(self, renderer)

# 绘制argmax()的第一段
xs = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
ys = [0.5, 0.4, 0.3, 0.2 , 0.1, 0.0]
zs = [0, 0, 0, 0, 0, 0]
fig = plt.figure()
ax = axisartist.Subplot(fig, 111)
ax = fig.add_axes((0.1,0.1,0.8,0.8), projection='3d')
ax.plot3D(xs, ys, zs, c='red', marker='o')
ys = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
xs = [0.5, 0.4, 0.3, 0.2 , 0.1, 0.0]
zs = [1, 1, 1, 1, 1, 1]
ax.plot3D(xs, ys, zs, c='blue', marker='o')
plt.xlim(0, 1)
plt.ylim(0, 1)
ax.view_init(azim=30, elev=30)
plt.show()

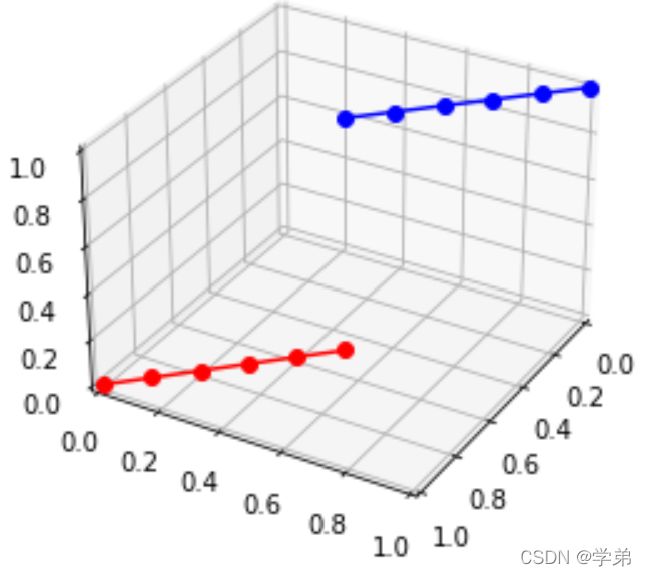
多元函数可微分的充分条件是函数连续且具有偏导数. 从argmax的三维图可以看出, argmax(x), 首先在x1 = x2处不连续,因此在该点处必定是不可导的. 在红线处, 保持x1不变, 求 y相对于x2的偏微分,发现是不存在的.因为x1不变的情况下,x2也是无法有一个微小的变动. 故, argmax()函数不可微分.

3. 引入随机性：gumbel分布

为了在y=argmax§中引入随机性, 将其修改为y = argmax(log§ + G).G称之为gumbel分布, 它的数学表达式为G=-log(-log($\xi$)))。引入该分布的作用是引入了随机性，且该随机性保证了该分布输出i的概率等于pi。下面是科学空间上的证明，比较容易理解。

4. 解决不可导：gumbel_softmax

1. 解决不可导的方法可以用gumbel_softmax来处理。也即forward阶段，使用argmax操作，暂时不用管后面反向操作;但在反向阶段则使用gumbel_softmax来做bp计算，可以通过看pytorch中相关代码块有一个很清晰的认知。

def gumbel_softmax(logits: Tensor, tau: float = 1, hard: bool = False, eps: float = 1e-10, dim: int = -1) -> Tensor:
    。。。
    gumbels = (
        -torch.empty_like(logits, memory_format=torch.legacy_contiguous_format).exponential_().log()
    )  # ~Gumbel(0,1)
    gumbels = (logits + gumbels) / tau  # ~Gumbel(logits,tau)
    y_soft = gumbels.softmax(dim)

    if hard:
        # Straight through.
        index = y_soft.max(dim, keepdim=True)[1]
        y_hard = torch.zeros_like(logits, memory_format=torch.legacy_contiguous_format).scatter_(dim, index, 1.0)
        ret = y_hard - y_soft.detach() + y_soft
    else:
        # Reparametrization trick.
        ret = y_soft
    return ret

2. 这样做是没有问题的，但是前向的y_hard,与y_softmax我们还是要尽可能缩小它们之间的“误差”，因此gumbel_softmax中引入了温度t, t越小，softmax就越接近One-hot。为了训练稳定性，一般t会取一个比较大的数字，然后逐步缩小。