深度学习——超参数的验证

前言

前文说到了由于训练数据少、神经网络复杂导致的过拟合，对于简单的网络可以采用权值衰减的方法拟制过拟合，但对于复杂的网络情况采用Dropout方法。
在神经网络中，除了权重和偏置等参数，超参数（hyper-parameter）也是一个常见的参数。包含以下内容：

神经元数量、batch 大小、参数更新时的学习率、权值衰减等。

超参数的设定直接影响模型的性能，设置超参数的过程也是一个漫长的试错过程，下文将介绍如何尽可能高效地寻找超参数的值。

验证数据

训练数据用于学习，测试数据用于评估泛化能力，由此判断模型是否过拟合。
不能使用测试数据评估超参数的性能。因为会造成超参数的值对测试数据发生拟合。
因此必须采用超参数专用的确认数据，用于调整超参数的数据，将该数据称为 验证数数据（validation data），用它来评估超参数的好坏。

训练数据用于参数（权重和偏置）的学习，验证数据用于超参数的性
能评估。为了确认泛化能力，要在最后使用（比较理想的是只用一次）
测试数据。

不同的数据集,有的会事先分成训练数据、验证数据、测试数据三
部分，有的只分成训练数据和测试数据两部分，有的则不进行分割。
用户需要自行进行分割。
如果是MNIST数据集，获得验证数据的
最简单的方法就是从训练数据中事先分割20%作为验证数据

(x_train, t_train), (x_test, t_test) = load_mnist()
#打乱训练数据,因为数据集的数据可能存在偏向
x_train, t_train = shuffle_dataset(x_train, t_train)
#分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]

def shuffle_dataset(x, t):
    """打乱数据集
    Parameters
    ----------
    x : 训练数据
    t : 监督数据
    Returns
    -------
    x, t : 打乱的训练数据和监督数据
    """
    permutation = np.random.permutation(x.shape[0])
    x = x[permutation,:] if x.ndim == 2 else x[permutation,:,:,:]
    t = t[permutation]

    return x, t

使用验证数据观察超参数的最优化方法

思路：
指一开始先大致设定一个范围，从这个范围中随机选出一个超参数（采样），用这个采样到的值进行识别精度的评估；然后，多次重复该操作，观察识别精度的结果，根据这个结果缩小超参数的“好值”的范围。

往往以以“10的阶乘”的尺度指定范围

贝叶斯最优化（Bayesian optimization）是一种对参数的最优化有很好作用的处理方式。

通俗点讲，就是在进行一次迭代的时候，先回顾下之前的迭代结果，结果太差的X附近就不去找了，尽量往结果好一点的X附近去找最优解，这样一来搜索的效率就大大提高了，这其实和人的思维方式也有点像，每次在学习中试错，并且在下次的时候根据这些经验来找到最优的策略。

超参数最优化的实现

以下将对 学习率和权值衰减系数 这两个超参数进行最优化处理。
超参数的随机采样的代码如下所示。
从0.001（10^−³）到 1000（10³）这样的对数尺度的范围中随机采样进行超参数的验证。这在Python中可以写成10 ** np.random.uniform(-3, 3)

weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)

现在就以权值衰减系数为10^-8 到 10^-4，学习率从10(-6)到10（-2）范围进行实验。

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

#为了实现高速化，减少训练数据
x_train = x_train[:500]
t_train = t_train[:500]

#分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]


def __train(lr, weight_decay, epocs=50):
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
                            output_size=10, weight_decay_lambda=weight_decay)
    trainer = Trainer(network, x_train, t_train, x_val, t_val,
                      epochs=epocs, mini_batch_size=100,
                      optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
    trainer.train()

    return trainer.test_acc_list, trainer.train_acc_list


#超参数的随机搜索======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
    # 指定搜索的超参数的范围===============
    weight_decay = 10 ** np.random.uniform(-8, -4)
    lr = 10 ** np.random.uniform(-6, -2)
    # ================================================

    val_acc_list, train_acc_list = __train(lr, weight_decay)
    print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
    key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
    results_val[key] = val_acc_list
    results_train[key] = train_acc_list

#绘制图形========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0

for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
    print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)

    plt.subplot(row_num, col_num, i+1)
    plt.title("Best-" + str(i+1))
    plt.ylim(0.0, 1.0)
    if i % 5: plt.yticks([])
    plt.xticks([])
    x = np.arange(len(val_acc_list))
    plt.plot(x, val_acc_list)
    plt.plot(x, results_train[key], "--")
    i += 1

    if i >= graph_draw_num:
        break

plt.show()

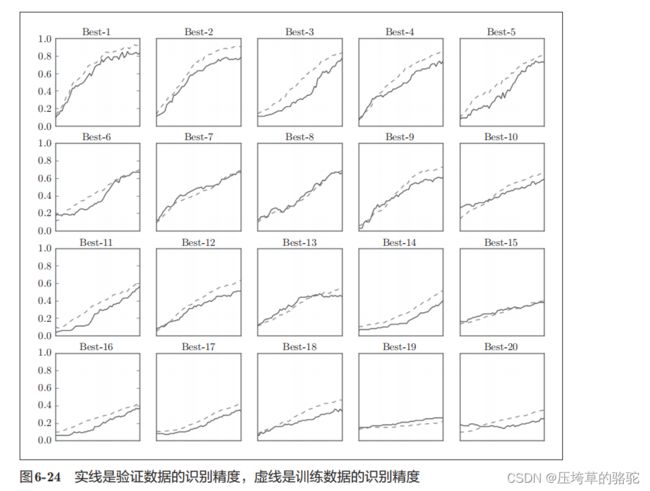
按识别精度从高到低的顺序排列了验证数据的学习的变化。
从图中可知，直到“Best-5”左右，学习进行得都很顺利。因此，我们来
观察一下“Best-5”之前的超参数的值（学习率和权值衰减系数），结果如下所示。

Best-1 (val acc:0.83) | lr:0.0092, weight decay:3.86e-07
Best-2 (val acc:0.78) | lr:0.00956, weight decay:6.04e-07
Best-3 (val acc:0.77) | lr:0.00571, weight decay:1.27e-06
Best-4 (val acc:0.74) | lr:0.00626, weight decay:1.43e-05
Best-5 (val acc:0.73) | lr:0.0052, weight decay:8.97e-06

学习率在0.001到0.01、权值衰减系数在10^−8到10−6之间时，学习可以顺利进行。
这样逐步缩小范围，找到一个最终超参数的值。

总结回顾

①参数的更新方法，常见的是SGD随机梯度下降法，还有Momentum、AdaGrad、Adam等方法。
②对于权重初始值的赋值方法对学习的过程十分重要
③权重初始值有以下：S形、关于原点对称的sigmoid函数跟tanh等函数可以采用Xavier初始值，ReLU函数可以考虑He初始值。
④考虑到权重的初始值的设定会对激活函数的输出值范围产生影响。通过使用Batch Normalization，可以使得输出的范围更广。
⑤由于训练数据太少、神经网络太复杂、表现力太强导致的过拟合，可以采用正则化技术：权值衰减、Dropout（当网络复杂的情况）等。
⑥超参数最优化的实现，逐渐缩小“好值”的范围。

参考

《深度学习入门：基于Python的理论与实现 》 斋藤康毅