【机器学习实战-11章】使用Apriori算法进行关联分析
使用Apriori算法进行关联分析
从大规模数据集中寻找物品间的隐含关系被称作关联分析(association analysis)
11.1 关联分析
-
优缺点
优点:易编码实现
缺点:在大数据集上可能较慢 -
关联分析是一种在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式:频繁项集或者关联规则。
1) 频繁项集(frequent item sets):经常出现在一块的物品的集合
2)关联规则(association rules):暗示两种物品之间可能存在很强的关系
3)支持度(support):定义为数据集中包含该项集的记录所占的比例。我们使用集合的支持度来度量其出现的频率。如豆奶的支持度为4/5,{豆奶,橙汁}的支持度为2/5.支持度是针对项集来说的,因此可以定义一个最小支持度,而只保留满足最小支持度的项集。
4)可信度或置信度(confidence)是针对一条诸如{尿布}—>{葡萄酒}的关联规则来定义的。这条规则的可信度被定义为“支持度({尿布,葡萄酒})/支持度({尿布})”。从图11-1中可以看到,由于{尿布,葡萄酒}的支持度为3/5,尿布的支持度为4/5,所以“{尿布}—>{葡萄酒}”的可信度为3/4=0.75。这意味着对于包含“尿布”的所有记录,我们的规则对其中75%的记录都适用。
11.2 Apriori原理
- 数字0,1,2,3代表四种不同的商品。 我们使用集合的支持度来度量某个项集(如(0,2))出现的频率。在上图中为4/15.
对于较大数据集,如果每个项集都要这么遍历的话效率太低。 为了降低所需的计算时间。使用Apriori算法。 - Apriori原理
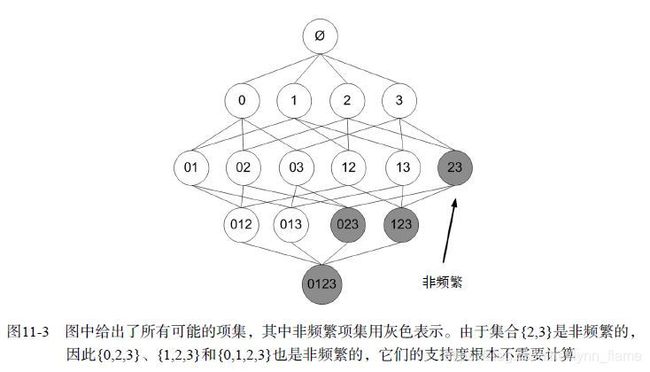
如果某个项集是频繁的,那么它的所有子集也是频繁的。反过来的话,如果一个项集是非频繁集,那么它的所有超集也是非频繁的。(apriori在拉丁语中指“来自以前”。当定义问题时,通常会使用先验知识或者假设,这被称为“一个先验(a priori)”)如下图所示
11.3 使用Apriori算法来发现频繁集
关联分析的目标包括两项:发现频繁集和发现关联规则。
Apriori算法是发现频繁集的一种方法。Apriori算法的两个输入参数分别是最小支持度和数据集。该算法首先会生成所有单个物品的项集列表,接着扫描交易记录来查看哪些项集满足最小支持度要求,去掉不满足最小支持度的集合。然后,对剩下的集合进行组合以生成包含两个元素的项集.接下来,再重新扫描交易记录,去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉。
11.3.1 生成候选项集
数据集扫描的伪代码:
对数据集中的每条交易记录tran
对每个候选项集can:
检查一下can是否是tran的子集
如果是,则增加can的计数值
对每个候选项集:
如果其支持度不低于最小值,则保留该项集
返回所有频繁项集列表
"""Apriori算法首先构建集合C1,然后扫描数据集来判断这些只有一个元素的项集是否
满足最小支持度的要求。那些满足最低要求的项集构成集合L1,而L1中的元素相互组合构成C2
,C2再进一步过滤变为L2.... """
#辅助函数
def loadDataSet():
return [[1,3,4],[2,3,5],[1,2,3,5],[2,5]]
def createC1(dataSet):
"""构建集合C1,C1是大小为1的所有候选集的集合。"""
C1 = [] #C1:list of list
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
C1.append([item]) #添加的是一个列表,目的是为每个物品项构建一个集合
C1.sort()
return list(map(frozenset,C1))
#对C1中每个项构建一个不变的集合,如果不转换为列表的话,辅助函数运行完最后返回的是一个空列表
#frozenset()函数返回一个冻结的集合,冻结后集合不能再添加或删除任何元素
#这里必须要使用frozenset而不是set类型,因为之后必须要将这些集合作为字典键值使用,使用frozenset可以实现这一点,而set却做不到。
def scanD(D,Ck,minSupport):
"""函数用于从C1生成L1,返回一个包含支持度值的字典
D:数据集
Ck:候选项集列表
minSupport:感兴趣项集的最小支持度"""
ssCnt = {}
#遍历数据集中的所有交易记录以及C1中所有候选集。如果C1中的集合是记录的一部分,那么增加字典中对应的计数值
for tid in D:
for can in Ck:
#issubset()用于判断集合的所有元素是否都包含在指定集合中,返回布尔值
if can.issubset(tid):
#__contains__判断集合是否在字典的键中
if not ssCnt.__contains__(can):
#if not ssCnt.has_key(can): python3使用__contains__()判断
ssCnt[can] = 1
else:
ssCnt[can] += 1
numItems = float(len(D)) #总的交易记录数
retList = []
supportData = {}
#计算每个集合的支持度
for key in ssCnt:
support = ssCnt[key]/numItems
if support >= minSupport:
retList.insert(0,key) #在列表的首部插入新的集合
supportData[key] = support
return retList,supportData
11.3.2 完整的Apriori算法
整个Apriori算法的伪代码如下:
当集合中项的个数大于0时:
构建一个K个项组成的候选项集的列表
检查数据以确认每个项集都是频繁的
保留频繁项集并构建k+1项组成的候选项集的列表
#Apriori算法
def aprioriGen(Lk,k):
"""创建Ck候选项集合
Lk:频繁项集列表
k:项集元素个数k
如Lk=[{0},{1},{2}],k=2
生成{0,1},{0,2},{1,2}"""
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1,lenLk):
#前k-2个项相同时,将两个集合合并
L1 = list(Lk[i])[:k-2]
L2 = list(Lk[j])[:k-2]
L1.sort();L2.sort()
if L1 == L2:
retList.append(Lk[i]|Lk[j])
return retList
def apriori(dataSet,minSupport = 0.5):
#创建初始大小为1的候选项集
C1 = createC1(dataSet)
D = map(set,dataset)
L1,supportData = scanD(D,C1,minSupport)
L = [L1]
k = 2
while (len(L[k-2]) > 0):
Ck = aprioriGen(L[k-2],k)
Lk,supK = scanD(D,Ck,minSupport)
supportData.update(supK)
L.append(Lk)
k += 1
return L,supportData
11.4 从频繁项集中挖掘关联规则
-
要找到关联规则,我们首先从一个频繁项集开始。我们直到集合中的元素是不重复的,但我们想知道基于这些元素能否获得其他内容。每个元素或者某个元素集合可能会推导出另一个元素。
-
我们再来看一下可信度的定义。
可信度或置信度(confidence)是针对一条诸如{尿布}—>{葡萄酒}的关联规则来定义的。这条规则的可信度被定义为“支持度({尿布,葡萄酒})/支持度({尿布})”。
如:频繁项集{豆奶,莴苣},那么就可能有一条关联规则“豆奶–>莴苣”。这意味着如果有人购买了豆奶,那么在统计上他会购买莴苣的概率较大。
前一节给出了频繁项集的量化定义,即它满足最小支持度要求。对于关联规则,我们也有类似的量化方法,这种量化指标称为可信度。一条规则P—>H的可信度定义为support(P|H)/support§.这里的P|H是指所有出现在集合P或者H中的元素,指的是并集操作。 -
如果某天规则并不满足最小可信度要求,那么该规则右部的所有子集也不会满足最小可信度要求。结果是可预见的,因为子集出现的可能性更低,每叠加一个物品,可能性都会降低。假设规则0,1,2–>3并不满足最小可信度要求,那么就知道任何左部为{0,1,2}子集的规则也不满足最小可信度要求。
-
类似于前述的Apriori算法,可以首先从一个频繁项集开始,接着创建一个规则列表,其中规则右部只包含一个元素,然后对这些规则进行测试。接下来合并所有剩余规则来创建一个新的规则列表,其中规则右部包含两个元素。这种方法又被称为分级法。
#关联规则生成函数
def generateRules(L,supportData,minConf=0.7):
"""L:频繁项集列表
supportData:包含那些频繁项集支持度数据的字典
minConf=0.7:最小可信度阈值
return bigRuleList:返回一个包含可信度的规则列表"""
bigRuleList = []
for i in range(1,len(L)): #只获取有两个或更多元素的集合
for freqSet in L[i]:
#遍历L中的每一个频繁项集并对每个频繁项集创建只包含单个元素集合的列表H1
H1 = [frozenset([item]) for item in freqSet]
#print(H1)
if (i > 1):#如果频繁项集的元素数目超过2,考虑进一步的合并
rulesFromConseq(freqSet,H1,supportData,bigRuleList,minConf)
else:
calcConf(freqSet,H1,supportData,bigRuleList,minConf)
return bigRuleList
def calcConf(freqSet,H,supportData,br1,minConf=0.7):
"""对规则进行评估可信度
返回一个满足最小可信度要求的规则列表"""
prunedH = []
#print(freqSet)
for conseq in H:
#print(conseq)
conf = supportData[freqSet]/supportData[freqSet-conseq] #support(A|B)/support(B)
if conf >= minConf:
print(freqSet-conseq,'--->',conseq,'conf:',conf)
br1.append((freqSet-conseq,conseq,conf))
#print(br1)
prunedH.append(conseq)
return prunedH
def rulesFromConseq(freqSet,H,supportData,br1,minConf=0.7):
"""生成候选规则集合
freqSet:频繁项集
H:出现在规则右部的元素列表H
supportData:包含那些频繁项集支持度数据的字典
br1=bigRuleList:generateRules的返回值"""
m = len(H[0])
#查看该频繁集是否大到可以移除大小为m的子集。如果可以的话,则将其移除
if len(freqSet) > (m+1):
#生成规则右部H的无重复组合,也就是包含所有可能的规则
Hmp1 = aprioriGen(H,m+1)
#测试可信度
Hmp1 = calcConf(freqSet,Hmp1,supportData,br1,minConf)
#如果不止一条规则满足要求,那么对Hmp1进行进一步组合
if len(Hmp1) > 1:
rulesFromConseq(freqSet,Hmp1,supportData,br1,minConf)
if __name__ == '__main__':
dataset = loadDataSet()
L,supportData = apriori(dataset)
print(L)
print(supportData)
rules = generateRules(L,supportData)
#print(rules)
11.5 示例:发现毒蘑菇的相似特征
我们的数据中,2 3 10 15 23 26 34 36 39 41 52 55 59 63 67 76 85 86 90 93 99 108 114
第一个特征表示有毒或者可食用,有毒值为2,否则为1.下一个特征是蘑菇伞的形状,有六种可能值,分别用3-8表示。
为了找到毒蘑菇中存在的公共特征,可以运行Apriori算法来寻找包含特征值为2的频繁项集。
def mushroom():
mushDatSet = [line.split() for line in open('./M_11_Apriori/mushroom.dat').readlines()]
L,supportData = apriori(mushDatSet,minSupport=0.3)
for item in L[3]:
if item.intersection('2'):
print(item)
11.7 本章小结
-
关联分析是用于发现大数据集中元素间有趣关系的一个工具,可以采用两种方式来量化这些有趣的关系。
第一种方式是使用频繁项集,它会给出经常在一起出现的元素项。
第二种方式是关联规则,每条关联规则意味着元素项之间的"如果……那么"关系。 -
Apriori原理是说如果一个元素项是不频繁的,那么那些包含该元素的超集也是不频繁的。算法从单元素项集开始,通过组合满足最小支持度要求的项集来形成更大的集合。支持度用来度量一个集合在原始数据中出现的频率。
-
每次增加频繁项集的大小,Apriori算法都会重新扫描整个数据集。当数据集很大时,这会显著降低频繁项集发现的速度。与Apriori算法相比,FP-growth算法只需要对数据库进行两次遍历,能够显著加快发现频繁项集的速度。



