图像分割(二)—— Segmenter: Transformer for Semantic Segmentation
Segmenter: Transformer for Semantic Segmentation
-
- Abstract
- 1. Introduction
- Our approach: Segmenter
-
- 3.1. Encoder
- 3.2. Decoder
Abstract
图像分割往往在图像 patch 的级别上模棱两可,并需要上下文信息达成标签一致。本文介绍了一种用于语义分割的 transformer 模型—Segmenter.
与基于卷积的方法相比,本文的方法允许在第一层和整个网络中建模全局上下文。以最近的 ViT 为基础,并将其扩展到语义分割。为此,本文依赖于与图像 patch 对应的输出嵌入,并使用逐点线性解码器(point-wise linear decoder)或一个 mask transformer 解码器从这些嵌入中获得类标签。本文利用了用于图像分类的预训练模型,并表明本文的模型可以在用于语义分割的中等规模数据集上微调它们,线性解码器已经可以获得优秀的结果,但性能可以由 mask transformer 产生类掩模进一步提高。
1. Introduction
最近的语义分割方法通常依赖于卷积编码器-解码器架构,其中编码器生成低分辨率图像特征,解码器对特征进行采样,以逐像素类分数分割地图。最先进的方法部署了全卷积网络 (FCN),并取得很好的结果。这些方法依赖于可学习的堆叠卷积,可以捕获语义丰富的信息。然而,卷积滤波器的局部特性限制了对图像中全局信息的访问。同时,这些信息对于分割尤为重要,局部 patches 的标记往往依赖于全局图像上下文。为了规避这个问题,DeepLab 引入了膨胀卷积的特征聚合和空间金字塔池。这样可以扩大卷积网络的接收域,获得多尺度特征。
随着自然语言处理的最新进展,一些分割方法探索了基于通道或空间注意和点方向注意的替代聚合方案,以更好地捕获上下文信息。
不足:然而,这样的方法仍然依赖于卷积 backbone,因此偏向于局部交互。广泛使用专门的层来纠正这种偏差,表明了卷积结构在分割方面的局限性。
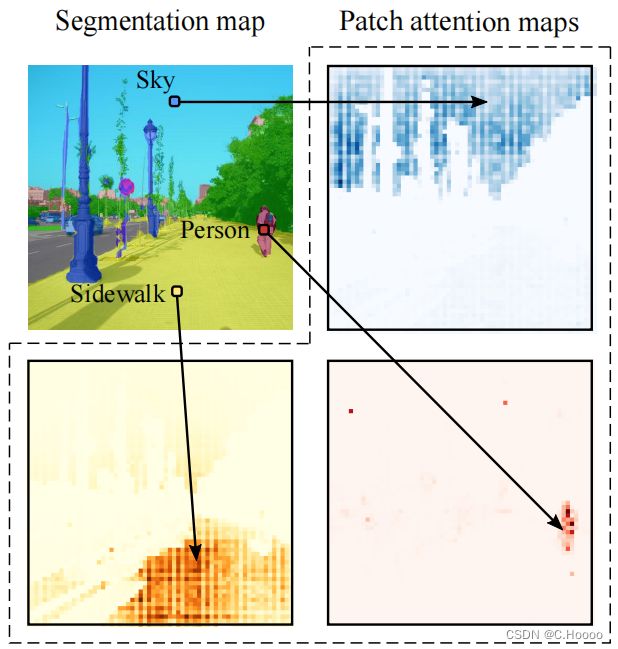
为了克服这些限制,本文将语义分割问题定义为序列到序列问题,并使用 transformer 架构在模型的每个阶段利用上下文信息。根据设计,transformer 可以捕获场景元素之间的全局交互,并且没有内置的感应先验,见图 1。然而,全局交互的建模需要二次方成本,这使得这些方法在应用于原始图像像素时非常昂贵。
继 Vision Transformers (ViT) 的最新研究之后,将图像分割成小块,并将线性小块嵌入作为 Transformers 编码器的输入 tokens。然后由 transformer 解码器将编码器产生的上下文化 tokens 序列上采样为逐像素类分数。对于解码,本文考虑一个简单的逐点线性映射的 patch 嵌入到类分数,或者一个基于 transformer 的解码方案,其中可学习的类嵌入与 patch tokens 一起处理以生成类 mask。我们通过消融模型正则化、模型大小、输入patch大小及其在精度和性能之间的权衡,对用于分割的变压器进行了广泛的研究。
本文所做工作如下:
- 我们提出了一种基于视觉转换器(ViT)的新的语义分割方法,该方法不使用卷积,通过设计捕获上下文信息,并且优于基于FCN的方法。
- 我们提出了一系列具有不同分辨率级别的模型,它允许在精度和运行时之间进行权衡,从最先进的性能到具有快速推理和良好性能的模型。
- 我们提出了一个基于变压器的解码器生成类掩模,它优于我们的线性基线,并可以扩展到执行更一般的图像分割任务。
- 我们证明了我们的方法在ADE20K[68]和Pascal Context[38]数据集上都产生了最先进的结果,并且在Cityscapes[14]上具有竞争力。
Our approach: Segmenter
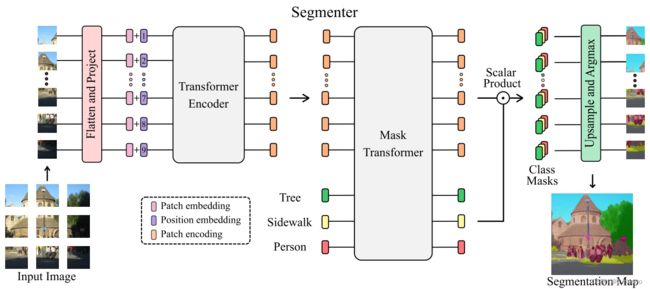
Segmenter 基于一个完全基于转换器的编码器-解码器架构,它将一系列 patch 嵌入映射到像素级的类注释。模型的概览如图 2 所示。patch 序列由第 3.1 节中描述的变压器编码器编码,并由第 3.2 节中描述的逐点线性映射或 mask Transformer 解码。本文的模型采用逐像素交叉熵损失的端到端训练。在推理时,上采样后应用 argmax,获得每个像素单类。
3.1. Encoder
一个图像 x ∈ R H × W × C x∈R^{H×W×C} x∈RH×W×C被分割成一个块序列 x = [ x 1 , . . . , x N ] ∈ R N × P 2 × C \mathbf{x}=[x_1,...,x_N]∈R^{N×P^2×C} x=[x1,...,xN]∈RN×P2×C
,其中 ( P , P ) (P,P) (P,P)是划分的块的大小, N = H W / P 2 N = H W / P^2 N=HW/P2 是块的数量,C是通道的数量。每个块被展平成一个一维向量,然后线性投影到一个patch embeddings,产生一个块嵌入序列 x 0 = [ E x 1 , . . . , E x N ] ∈ R N × D x_0=[E_{x_1},...,E_{x_N}]∈R^{N×D} x0=[Ex1,...,ExN]∈RN×D,其中 E ∈ R D × ( P 2 C ) E∈R^{D×(P^2C)} E∈RD×(P2C). 为了获取位置信息,将可学习的位置嵌入 pos = [ p o s 1 , . . . , p o s N ] ∈ R N × D \text{pos}= [ pos_1 , . . . , pos_N ] ∈ R^{N × D} pos=[pos1,...,posN]∈RN×D 添加到块序列中,得到token z 0 = x 0 + p o s z_0=x_0+pos z0=x0+pos的输入序列。
将由L层组成的transformer编码器应用于标记 z 0 z_0 z0 的序列,生成上下文化编码 z L ∈ R N × D z_L∈R^{N×D} zL∈RN×D 序列。transformer层由一个多头自注意(MSA)块组成,然后是一个由两层组成的点向MLP块组成,在每个块之前应用LayerNorm(LN),在每个块之后添加残差块。
3.2. Decoder
块编码序列 z L ∈ R N × D z_L∈R^{N×D} zL∈RN×D 被解码为分割映射 s ∈ R H × W × K s∈R^{H×W×K} s∈RH×W×K,其中K为类数。解码器学习将来自编码器的patch级编码映射到patch级的类分数。接下来,这些patch级类分数通过线性插值双线性插值上采样到像素级分数。我们将在下面描述一个线性解码器,它作为一个基线,而我们的方法是一个掩码转换器,见图2。
Linear 对块的编码 z L ∈ R N × D z_L∈R^{N×D} zL∈RN×D应用点向线性层,产生块级类对数 z l i n ∈ R N × K z_{lin}∈R^{N×K} zlin∈RN×K. 然后将序列重塑为2D特征图 s l i n ∈ R H / P × W / P × K s_{lin}∈R^{H/P×W/P×K} slin∈RH/P×W/P×K,并提前上采样到原始图像大小 s ∈ R H × W × K s∈R^{H×W×K} s∈RH×W×K. 然后在类维度上应用softmax,得到最终的分割映射。
Mask Transformer 对于基于transformer的解码器,我们引入了一组K个可学习的类嵌入 c l s = [ c l s 1 , . . . , c l s K ] ∈ R K × D cls=[cls_1,...,cls_K]∈R^{K×D} cls=[cls1,...,clsK]∈RK×D, 其中K是类的数量。每个类的嵌入都被随机初始化,并分配给一个语义类。它将用于生成类掩码。类嵌入cls由解码器与补丁编码 z L z_L zL联合处理,如图2所示。解码器是一个由M层组成的transformer编码器。我们的mask transformer 通过计算解码器输出的 L 2 L_2 L2 标准化patch嵌入 z M ′ ∈ R N × D z^{\prime}_M∈R^{N×D} zM′∈RN×D 与类嵌入 c ∈ R K × D c∈R^{K×D} c∈RK×D之间的标量乘积来生成K个掩码。类掩码的集合计算如下:
M a s k s ( z M ′ , c ) = z M ′ c T (4) Masks(z^{\prime}_M,c)=z^{\prime}_Mc^T\tag{4} Masks(zM′,c)=zM′cT(4)
其中, M a s k s ( z M , c ) ∈ R N × K Masks(z_M,c)∈R^{N×K} Masks(zM,c)∈RN×K 是一组块序列。然后将每个mask序列重塑为二维mask,形成 s m a s k ∈ R H / P × W / P × K s_{mask}∈R^{H/P×W/P×K} smask∈RH/P×W/P×K, 并提前上采样到原始图像大小,获得特征图 s ∈ R H × W × K s∈R^{H×W×K} s∈RH×W×K. 然后在类维度上应用一个softmax,然后应用一个层范数,得到像素级的类分数,形成最终的分割图。