【简易笔记】计算机视觉与深度学习(全连接神经网络、卷积) EP2
本篇承接上文:计算机视觉与深度学习 EP1
本篇主要内容:
全连接神经网络(P4 - P6)
卷积与卷积神经网络(P7 - P8)
经典网络分析(P9 - P10)
可视化(P12 - P13)
主要资料来源:
计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
PyTorch参考网站:
PyTorch
知识框架:

————————————————————————————————————————————————————————
全连接神经网络
这里就用一个两层全连接神经网络来举一个例子
两层全连接神经网络
下面是两层全连接神经网络的数学表达式:
f = W 2 m a x ( 0 , W 1 x + b 1 ) + b 2 f=W_{2}max(0,W_{1}x+b_{1})+b_{2} f=W2max(0,W1x+b1)+b2
好理解的是,W1这一组参数对应着第一层神经网络,经过一层得出权值后,在用第二层神经网络对第一层输出的值再进行学习,即学习到W2对应的参数组
两层全连接示意图: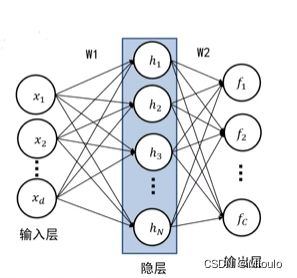
tips: 网络中如果缺少了非线性激活函数(比如常用的ReLu激活函数,下面给出常用的激活函数),这个全连接神经网络就会变成一个线性分类器
常见的激活函数: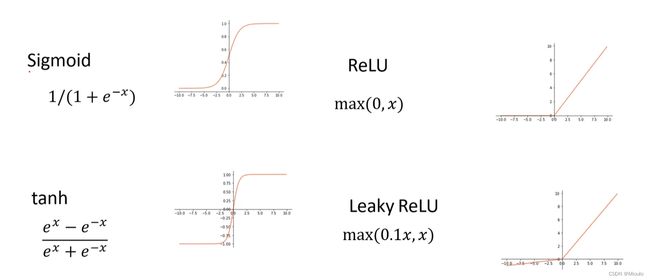
————————————————————————————————————————————————————————
网络结构设计
在设计神经网络时会有深度设计和宽度设计两方面的问题
深度设计,即隐藏层数目的设计(感觉就是何时提取特征激活,要提取几次特征的问题)
宽度设计,即每个隐藏层设置几个神经元比较合适(即模板个数即提取出几个特征值)
示意图:

tips:实际上,这个20个隐层神经元的模型就可以理解成已经是一种过拟合的模型了,在对这组数据进行分类时,如果设置的参数过多,模型的泛化能力减弱,变成了只是“记忆”下这个数据集的模型,而不是我们想要的“学习”了这个数据集。解决过拟合有两种比较常用的方法,分别是正则化和随机失活,后文会详细总结
————————————————————————————————————————————————————————
L2正则化
R ( W ) = ∑ k ∑ l W k , l 2 R(W)=\sum_{k}^{}\sum_{l}^{}W_{k,l}^{2} R(W)=k∑l∑Wk,l2
解读这个公式,即是惩罚集中的权值模板
当这个权值模板权值集中时,这个R(W)损失会远大于分散的模板
由此用这个正则损失鼓励机器学习分散的权值模板,从而使及其最大程度使用输入的值进行决策
提高模型的泛化能力
这个正则化会有一个正则化强度的超参数,很好理解
————————————————————————————————————————————————————————
随机失活
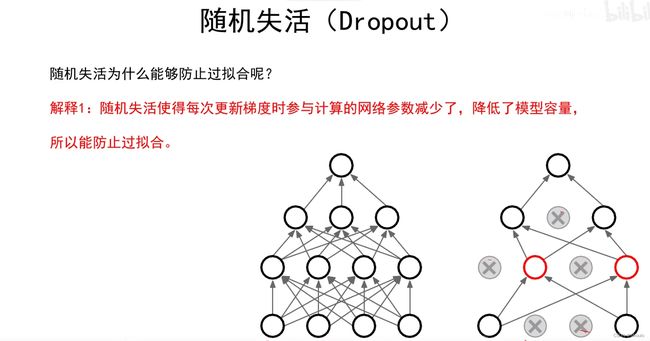
如图所示,在设置随机失活时会有一个随机失活比率,这是一个超参数,通常把这个值设置在0.2-0.5

这就是一个随机失活的实例,p即为随机失活比率,U1层即是第一层随机失活层,在这里可以看到会把1/2(期望)的权值归0(即失活)
看代码会发现U1中值都是0和1,即时0代表失活,1代表神经元正常工作
————————————————————————————————————————————————————————
SOFTMAX
在经过输入层,隐藏层之后,在输出层时,有时候会用SOFTMAX进行归一化,然后再进行输出,能直观地得到该模型进行这次决策的正确的概率(即可以很方便地用百分率表示)
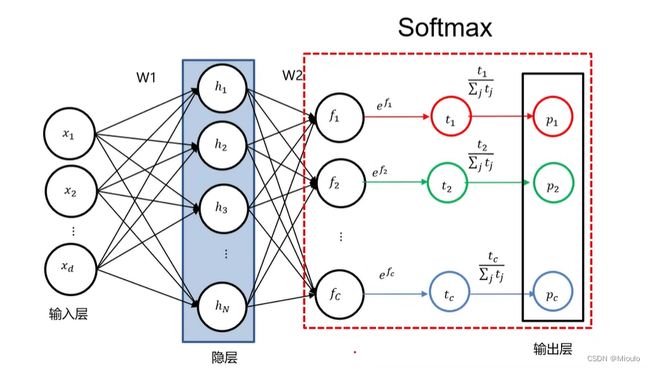
实际案例如下展示:

————————————————————————————————————————————————————————
交叉熵损失
交叉熵损失用于度量分类器输出与预测值之间的距离
交叉熵是一个信息量的概念
就信息量这个概念,粗略的说,是用来衡量这个事件蕴含信息多少的量
比如中国男足赢得了世界杯,这个事件本身极小概论发生,但如果它发生了,那这个事件蕴含的信息则是巨大的(举个反例,太阳照常升起就是一个信息量很低的事件)
再转回机器学习,我们用这个交叉熵损失来衡量现在这个神经网络作出的决策与真正的情况之间还有多少差距,换句话说,就是这个模型对这个数据集学习到了什么程度(或者说是这批数据集对这个模型还蕴含着多少信息,还有多少学习的价值)
以上只是在看视频和自己做小程序时的简单的理解,可能会有差错
由于交叉熵损失与之前介绍的多类支撑向量机损失相比,有很多的优点,所以之后常用交叉熵损失(我之前上传的那个区分Vtuber的程序也是用的交叉熵损失)
参考视频(P4 位置00:40:12):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
参考文章:交叉熵损失函数
————————————————————————————————————————————————————————
反向传播与计算图
这部分在实践时PyTorch会进行自动运算,应用时只需要查阅对应函数及其参数即可,所以大致了解
参考视频(P4 位置 01:02:20):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
在传递梯度时,经常会遇见两个问题:梯度消失和梯度爆炸
在激活函数中可以体现为(用二维图像解释,梯度消失即是导数为0,这会导致无法传递任何信息,模型无法更新,梯度爆炸则是导数趋于无穷,会直接把模型权值大幅度变化,使得无法有效学习更新参数)

————————————————————————————————————————————————————————
权值初始化
为了避免梯度消失和梯度爆炸情况的出现,我们要进行正确的权值初始化
.
Xavier初始化

MSRA初始化
参考视频(P5 位置 01:20:20):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
————————————————————————————————————————————————————————
批归一化
换一种思路的话,在下一层的每个神经元的输出这批进行处理来解决梯度爆炸和梯度消失问题

想了解的话见下文链接
参考视频(P5 位置 01:26:20):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
————————————————————————————————————————————————————————
梯度算法改进
这部分讲解了几种梯度下降的算法,内容比较多,我的理解也不深
所以在这里放出算法名然后给出参考链接
tips:之前我的那个识别Vtuber的文章里用到的就是SGD梯度下降优化算法,感兴趣的可以去看看
动量法

参考视频(P5 位置 00:44:17):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
自适应梯度法和RMSProp
参考视频(P5 位置 00:53:22):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
Adam算法
参考视频(P5 位置 01:02:22):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
超参数优化
学习率是一个很重要的超参数,会影响模型的收敛速度
通常采用随机搜索的超参数优化方法(因为可以尝试更多的学习率)

————————————————————————————————————————————————————————
卷积与卷积神经网络
卷积(概念介绍)
参考视频通过对噪声图像消澡来引入卷积和卷积核的概念(这里将数学公式略过)
如图

其中,就是通过卷积核和图片中的对应像素进行运算后才得到这个中间像素的值
这个图的卷积核是

运算示意图为
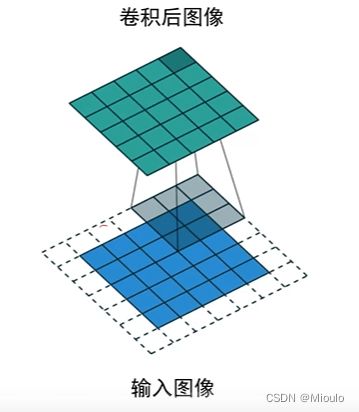
tips:卷积具有叠加性和平移不变性的特点
————————————————————————————————————————————————————————
图像填充
为了使卷积前后图片的大小不变,我们通常进行边界填充
下面是0填充、拉伸填充和镜像填充


————————————————————————————————————————————————————————
卷积核
高斯卷积核
我们通过高斯卷积核对图像进行平滑 (如果用平均卷积核进行处理会出现横纹和竖纹)
高斯卷积核方差:
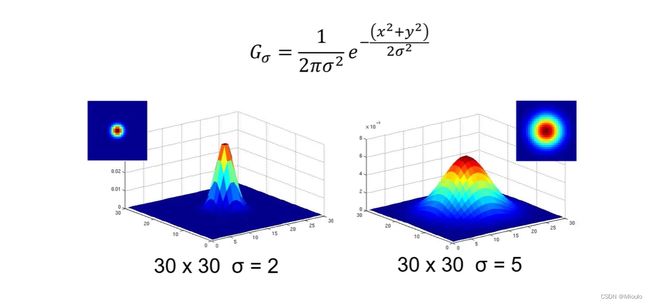
平滑效果如图所示,方差大的平滑效果好,反之
————————————————————————————————————————————————————————
高斯卷积核尺寸:
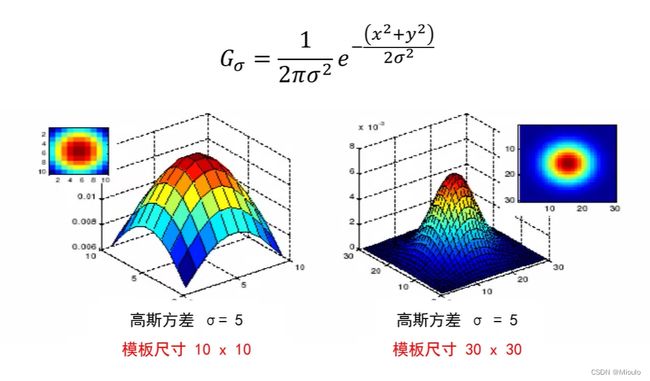
这里是尺寸越大,平滑效果越好
tips:对于高斯噪声用高斯卷积核可以进行降噪,但是对于椒盐噪声和脉冲噪声时用中值滤波器则可
————————————————————————————————————————————————————————
边缘提取
之前直接用OpenCV的Canny提取
参考视频(P7 位置 01:07:22):计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集
————————————————————————————————————————————————————————
卷积神经网络
卷积神经网络
传统神经网络只是适合处理小图像,如果图像过大会使效率变得很低
而卷积神经网络处理时参数远远小于传统神经网络
下面是该神经网络大致的结构

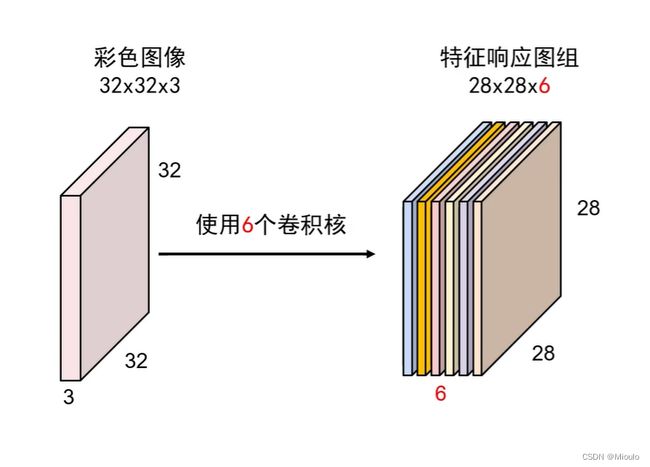
对于卷积神经网络的卷积核会与之前的卷积核有些不同,这里的卷积核中还会有偏置

还可以将多个卷积核编成一个卷积核组,如图
————————————————————————————————————————————————————————
卷积核组
在设计卷积核组之后,对图像进行卷积操作之后可以得到特征响应图,在之后可视化部分可以将特征相应图可视化

————————————————————————————————————————————————————————
卷积核尺寸、步长与组中卷积核个数
如果没有边界填充

考虑到边界填充的情况下

考虑到每组多个卷积核与输出特征图尺寸

————————————————————————————————————————————————————————
池化

————————————————————————————————————————————————————————
最大池化和平均池化
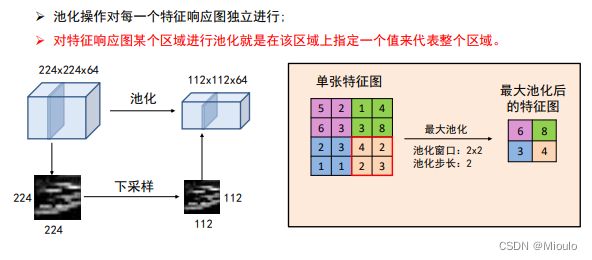
平均池化很好理解,就是将每个像素点平均后输出则可
————————————————————————————————————————————————————————
全连接层(FC)
与之前的传统神经网络一样,见之前的内容



