基于麻雀搜索算法优化的广义回归神经网络(GRNN)预测 -附代码

基于麻雀搜索算法优化的广义回归神经网络(GRNN)预测

摘要：本文介绍基于麻雀搜索算法优化的广义神经网络(GRNN)预测，并将其应用于货物量预测

1.GRNN 神经网络概述

广义回归神经网络 CGRNN, Generalized Regression Neural Network）是美国学者 Don­aid F. Specht 在 1991 年提出的，它是径向基神经网络的一种。 GRNN 具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性，适用于解决非线性问题。 GRNN在逼近 能力和学习速度上较 RBF 网络有更强的优势，网络最后收敛于样本量积聚较多的优化回归 面，并且在样本数据较少时，预测效果也好。此外，网络还可以处理不稳定的数据。因此， GRNN 在信号过程、结构分析、教育产业、能源、食品科学、控制决策系统、药物设计、金融领域、生物工程等各个领域得到了广泛的应用 。

2.GRNN 的网络结构

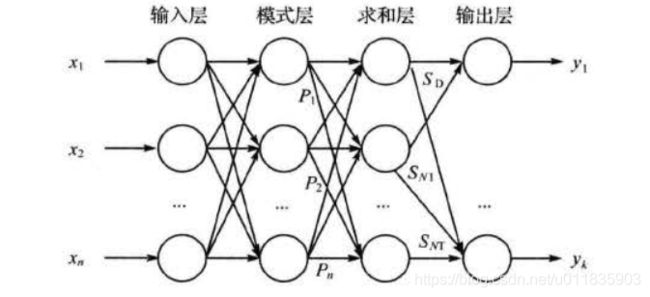
GRNN 在结构上与 RBF 网络较为相似。它由四层构成，如图1所示，分别为输入层(input layer）、模式层（ pattern layer）、求和层 （ summation layer）和输出层（ output layer）。对 应网络输入 $X=[x_1,x_2,...,x_n{]}^T$，其输出为 $Y=[y_1,y_2,...,y_n{]}^T$ 。

图1 .GRNN网络结构

(1)输入层

输入层神经元的数目等于学习样本中输入向量的维数，各神经元是简单的分布单元，直接将输入变量传递给模式层。

(2)模式层

模式层神经元数目等于学习样本的数目 η ，各神经元对应不 同的样本，模式层神经元传递函数为：
$$p_i=exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]i=1,2,...,n\text{\hspace{1em}(1)}$$
神经元 $i$ 的输出为输入变量与其对应的样本 $X$ 之间 Euclid 距离平方的指数平方 $D_i^2＝(X-X_i{)}^T(X-X_i）$ 的指数形式 。式中， $X$ 为网络输入变量； $X_i$ 为第 i 个神经元对应的学习样本。

(3)求和层

求和层中使用两种类型神经元进行求和。

一类的计算公式为${\sum }_{i=1}^{n}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]$,它对所有模式层神经元的输出进行算术求和，其模式层与各神经元的连接权值为1 ，传递函数为:
$$S_D=\sum _{i=1}^n{P}_i\text{\hspace{1em}(2)}$$
另 一类计算公式为${\sum }_{i=1}^n{Y}_{i}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]$,它对所有模式层的神经元进行加权求和，模式层中第 i 个神经元与求和层中第 j 个分子求和神经元之间的连接权值为第 i 个输 出样本$Y_i$中的第 j 个元素，传递函数为:
$$S_{Nj}=\sum _{i=1}^n{y}_{ij}{P}_i,j=1,2,...,k\text{\hspace{1em}(3)}$$
(4）输出层

输出层中的神经元数目等于学习样本中输出向量的维数h ，各神经元将求和层的输出相除 ， 神经元 j 的输出对应估计结果Y( X） 的第 j 个元素，即：
$$y_j=\frac{S_{Nj}}{S_D},j=1,2,...,k\text{\hspace{1em}(4)}$$

3.GRNN的理论基础

广义回归神经网络的理论基础是非线性回归分析 ， 非独立变量 Y 相对于独立变量x的回归分析实际上是计算具有最大概率值的 y. 设随机变量x和随机变量 y 的联合概率密度函数 为f(x,y)，已知 x 的观测值为 X ，则 y 相对于 X 的回归，也即条件均值为:

KaTeX parse error: \tag works only in display equations

Y即为在输入为 X 的条件下，Y 的预测输出 。

应用 Parzen 非参数估计，可由样本数据集${x_i,y_i}_{i=1}^n$估算密度函数$f^{\prime }(X,y)$
$$f^{\prime }(X,y)=\sum _{i=1}^{n}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]exp[-\frac{(X-Y_i{)}^2}{2{\sigma }^2}]/(n(2\pi {)}^{\frac{p+1}{2}}{\sigma }^{p+1})\text{\hspace{1em}(6)}$$
式中，$X_i$，$Y_i$， 为随机变量 x 和 y 的样本观测值;$n$为样本容量；$p$为随机变量 $x$的维数；$\sigma$为高斯函数的宽度系数，在此称为光滑因子。

用$f(X,y)$代替 $f(X,y)$代人式，并交换积分与加和的顺序:
$$Y(X)=\frac{{\sum }_{i=1}^{n}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]{\int }_{-\infty }^{\infty }yexp[-(Y-Y_i{)}^2/(2{\sigma }^2)]dy}{{\sum }_{i=1}^{n}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]{\int }_{-\infty }^{\infty }exp[-(Y-Y_i{)}^2/(2{\sigma }^2)]dy}\text{\hspace{1em}(7)}$$
由于${\int }_{-\infty }^{\infty }z{e}^{-x^2}dz=0$，对两个积分进行计算后可得网络的输出Y(X）为：
$$Y(X)=\frac{{\sum }_{i=1}^n{Y}_{i}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]}{{\sum }_{i=1}^{n}exp[-\frac{(X-X_i{)}^T(X-X_i)}{2{\sigma }^2}]}\text{\hspace{1em}(8)}$$
估计值$Y(X)$为所有样本观测值$Y_i$的加权平均，每个观测值$Y_i$的权重因子为相应的样本$X_i$与 $X$之间 Euclid 距离平方的指数 ． 当光滑因子 σ 非常大的时候 ，$Y(X)$近似于所有样本因变量的均值 。 相反，当光滑因子σ 。趋向于0 的时候， $Y(X)$和训练样本非常接近，当需预测的点被包含在训练样本集中时，公式求出的因变量的预测值会和样本中对应的因变量非常接近， 而一旦碰到样本中未能包含进去的点，有可能预测效果会非常差 ， 这种现象说明网络的泛化能力差。当σ取值适中，求预测值$Y(X)$时，所有训练样本的因变量都被考虑了进去，与预测点距离近的样本点对应的因变量被加了更大的权。

4.运输系统货运量预测相关背景

运输系统作为社会经济系统中的一个子系统，在受外界因素影响和作用的同时 ， 对外部经济系统也具有一定的反作用，使得运输需求同时受到来自运输系统内外两方面因素的影响。 作为运输基础设施建设投资决策的基础，运输需求预测在国家和区域经济发展规划中，具有十分重要的作用，其中，由于货物运输和地方经济及企业发展的紧密联系，货运需求预测成为货 运需求和经济发展关系研究中的一个重要问题 。因此，作为反映货物运输需求的一项重要指标，货运量预测研究和分析具有较强的实际和理论意义 ．

在此情况下，国内一些学者将神经网络引入到货运量预测中来。GRNN 在逼近能力、分类能力和学习速度方面具有较强优势 ， 网络最后收敛于样本量积聚最多的优化回归面，并且在数据缺乏时效果也较好。网络可以处理不稳定的数据 ， 因此本案例采用 GRNN 建立了货运量预测模型 ， 并利用历史统计数据对货运量进行预测 。

5.模型建立

根据货运量影响因素的分析，分别取国内生产总值（ GDP）、工业总产值、铁路运输线路长度、复线里程比重、公路运输线路长度、等级公路比重、铁路货车数量和民用载货汽车数量 8 项 指标因素作为网络输入，以货运总量、铁路货运量和公路货运量 3 项指标因素作为网络输出 ， 构建 GRNN。本案例中 data. mat 中共有 p, t 两组数据 ，又各含 13 组数据，代表了 1996-2008 年的货 运量和与其相关的各个变量值。将 p、t 的前 12 组数据作为网络的训练数据，最后 1 组数据作 为网络的预测数据，建立 GRNN 神经网络对货运量进行预测。

6.麻雀搜索算法优化GRNN

麻雀搜索算法的具体原理参考博客：https://blog.csdn.net/u011835903/article/details/108830958。

网络训练时，采用交叉验证的方式，优化参数主要是GRNN的光滑因子$\sigma$参数。是适应度函数设计为：
$$fitness=argmin(MS{E}_{pridect})$$
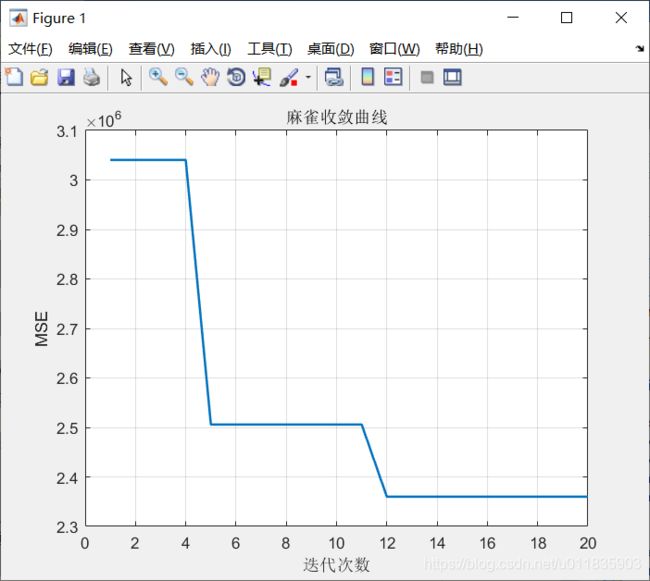
适应度函数选取训练后的MSE误差。MSE误差越小表明预测的数据与原始数据重合度越高。最终优化的输出为，最佳训练集以及对应的光滑因子。

7.实验结果

麻雀搜索算法的参数设置如下：

%% 麻雀搜索算法
pop = 20;%种群数量
Max_iteration = 20;%最大迭代次数
lb = 0.1;%下边界
ub = 2;%上边界
dim = 1;%维度
fobj = @(spread) fun(spread,p_train,t_train,indices);

经过麻雀搜索算法优化的结果：

最佳训练集信息：
此时最佳输入值为

desired_input =

   -1.0000   -0.8993   -0.7948   -0.2955   -0.0574    0.3838    0.6652    0.8767    1.0000
   -0.9998   -1.0000   -0.1291    0.2070    0.3417    0.6187    0.7838    0.9372    1.0000
   -1.0000   -0.8616   -0.4969    0.1950    0.3333    0.6478    0.6604    1.0000    1.0000
   -1.0000   -0.5385   -0.0769    0.2308    0.3846    0.6923    0.6923    1.0000    1.0000
   -1.0000   -0.9429   -0.9175   -0.5937   -0.3270    0.2508    0.5619    0.7333    1.0000
   -1.0000   -1.0000   -1.0000   -0.3000   -0.2000    0.2000    0.5000    0.8000    1.0000
    0.0141   -1.0000    0.0187    0.2477    0.3682    0.6195    0.7735    0.8635    1.0000
   -1.0000   -0.9211   -0.8826   -0.7786   -0.6099   -0.0318    0.2843    0.5891    1.0000

此时最佳输出值为

desired_output =

   -1.0000   -0.9839   -0.9838   -0.4503   -0.2463    0.2862    0.5394    0.7787    1.0000
   -1.0000   -0.9040   -0.8604   -0.3950   -0.2293    0.2124    0.4116    0.7228    1.0000
   -1.0000   -0.8020   -0.8042   -0.2471   -0.0500    0.2505    0.4693    0.8308    1.0000

GRNN神经网络三项流量预测的误差为13244.4881      4211.69012      15766.2697

未经过麻雀搜索的结果为：

GRNN神经网络三项流量预测的误差为28106.967 15245.9913 21653.0687（数据来源于《MATLAB神经网络43个案例分析》）

从结果来看，麻雀优化后取得的结果GRNN神经网络三项流量预测的误差为13244.4881 4211.69012 15766.2697明显更优，误差大大减少。

8.参考文献

书籍《MATLAB神经网络43个案例分析》

9.Matlab代码

[基于麻雀搜索算法优化的广义回归神经网络(GRNN)预测]
[基于鲸鱼算法优化的广义回归神经网络(GRNN)预测]
个人资料介绍