OpenCV中SGBM中BT代价计算

AD算法

在对BT算法说明前，先对AD（Absolute differences）算法进行简单说明。

如上图所示，$I_R(x,y)$、$I_T(x,y)$分别表示左图和右图中的像素$(x,y)$处的值，那么左图中像素$I_R(x,y)$与右图中视差为$d$的像素的AD代价值如下式所示：
$$c(x,y,d)=|I_R(x,y)-I_T(x+d,y)|$$

BT算法

BT的代价也是像素灰度值差值的绝对值，不同之处在于BT利用了亚像素的灰度信息。

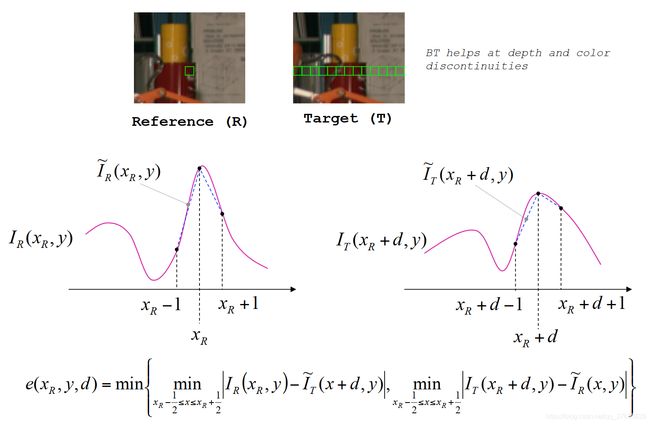
如图所示，首先计算左图中像素$(x_R-0.5,y)$和$(x_R+0.5,y)$之间亚像素位置$(x_R+x,y)$的灰度值$I_R(x_R,y)$,然后计算右图中像素$(x_R+d-0.5,y)$和$(x_R+d+0.5,y)$之间亚像素位置$(x_R+d+x,y)$的灰度值$I_T(x_R+d,y)$。
分别计算两个代价：
$$co{s}_1=\underset{x_R-\frac{1}{2}\le x_R+\frac{1}{2}}{\min }|I_R(x_R,y)-I_T(x_R+d,y)|$$ $$co{s}_2=\underset{x_R-\frac{1}{2}\le x_R+\frac{1}{2}}{\min }|I_T(x_R+d,y)-I_R(x_R,y)|$$最终的代价为两个代价的最小值：
$$cos=min(co{s}_1,co{s}_2)$$
注意：Opencv源码中，并没有计算太多亚像素的灰度值，只是取了两个像素中间点的亚像素的灰度值。

 for( int d = minD; d < maxD; d++ )
 {
      int v = prow2[width-x-1 + d];// 之前右图是逆序存储，现在需要逆序取出，并加上视差值
      int v0 = buffer[width-x-1 + d];// 最小值
      int v1 = buffer[width-x-1 + d + width2];// 最大值
      int c0 = std::max(0, u - v1); c0 = std::max(c0, v0 - u);
      int c1 = std::max(0, v - u1); c1 = std::max(c1, u0 - v);
      // cost计算。与原论文不同的是，opencv的B.T. metrics包含了两个部分，
     // 一部分为prow1和prow2第一行所存储的左右图的sobel滤波结果的B.T. metrics，
     // 一部分为prow1和prow2第二行所存储的左右图的灰度值的B.T. metrics
      cost[x*D + d] = (CostType)(cost[x*D+d] + (std::min(c0, c1) >> diff_scale));
  }