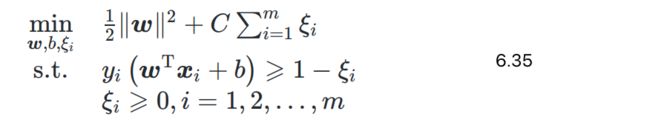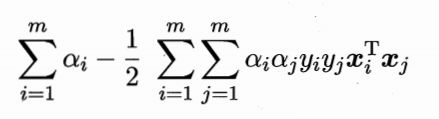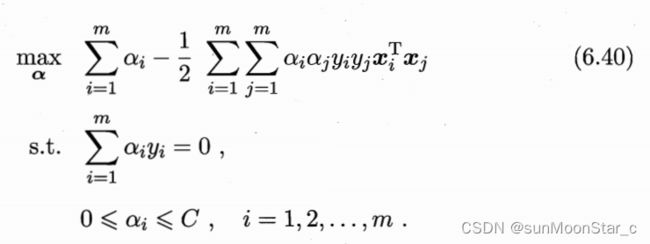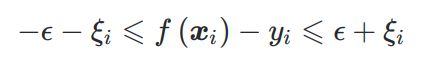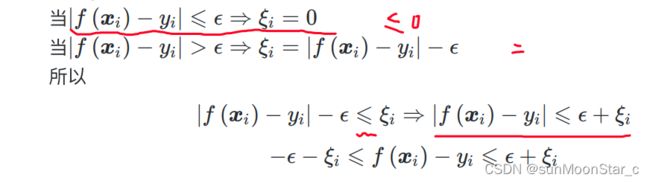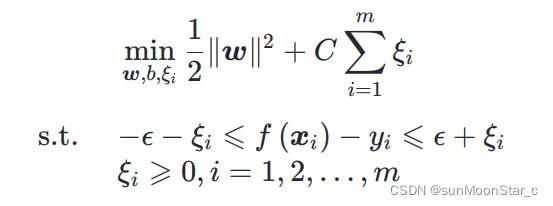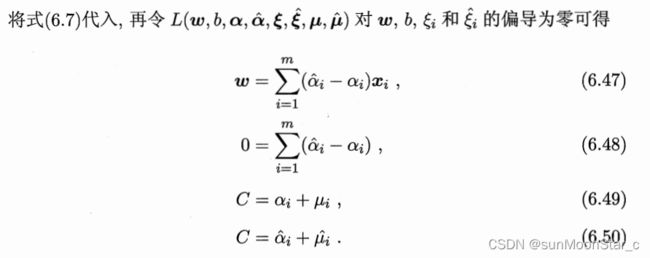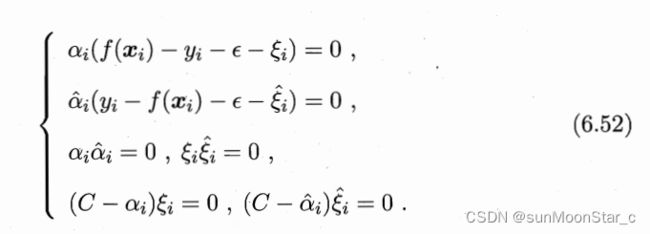机器学习西瓜书笔记:软间隔和支持向量回归SVR
1、首先由SVM问题(最大间隔超平面模型):所有样本都可以正确分类的最优化问题,引入软间隔SVM(允许分类错误)的最优化问题,即需要添加损失函数(样本不满足约束的程度,或者说分类错误的程度),然后最优化。
- 这里强调一下:超平面这个回归模型如何实现分类功能:套上sign函数。
- 损失函数要找性质好的,即凸函数,连续
- 损失函数不要单纯只反映分类正确和错误(0/1损失函数)。而是分类正确时,损失记为0,分类错误时体现损失的程度1-z。则hinge损失函数可以实现。
- 然后用松弛变量表示损失函数的取值
- 求解拉格朗日对偶问题
2、再引入SVR,针对回归问题如何求一个间隔带回归模型,使得预测值f和真实标记y差距(即损失)最小化。
- 间隔带内允许 ϵ \epsilon ϵ的误差,都算作没有损失,即最小化的是|f-y| - ϵ \epsilon ϵ,则引入不敏感损失函数
SVR这个回归问题的最优化问题,形式要往软间隔SVM形式靠拢,就可以用其求解方法,比如转化为对偶问题。
一、软间隔soft margin
引入软间隔的概念,把SVM硬间隔问题转化为软间隔问题求解,则能够在非线性可分数据集上(即允许有样本分类错误),解出损失(样本不满足约束程度)最小的SVM超平面模型。
1.1 为何引入软间隔
在现实任务中,线性不可分的情形才是最常见的,退一步说,即使恰好找到了某个核函数使得训练集在特征空间中线性可分,特很难断定这个貌似线性可分的结果是否是过拟合造成的。因此需要允许支持向量机犯错,引入软间隔
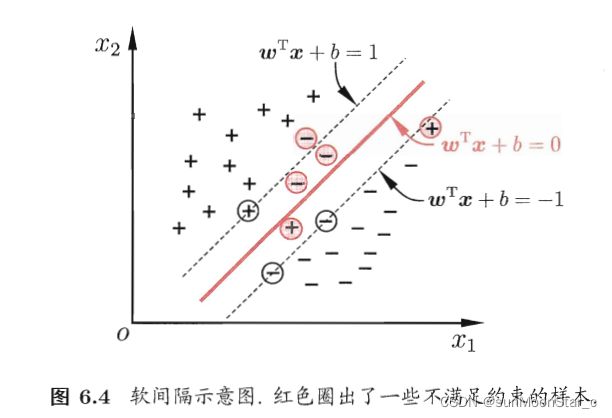
1.2 软间隔
数学角度,软间隔就是允许部分样本(尽可能少)不满足如下的约束条件:
不满足6.28约束的几何意义:样本 x ⃗ i \vec{x}_i xi被分类错误,到超平面的集合距离负数,也就是6.28的左边是负数,自然肯定不会>=我们规定的正确分类的正数间隔。
1.3 损失函数 ℓ \ell ℓ需要满足的3个特点
把是否满足约束条件的问题转化为损失:
1、满足约束条件的样本:损失为0
2、不满足约束条件的样本:损失不为0
- 0/1损失函数满足1,2
3、(可选)损失和违反约束条件的程度成正比
- 替代损失函数,例如hinge都满足。
- SVR用的不敏感损失函数也满足这3条
满足以上要求,我们最小化损失,就相当于最小化不满足约束条件的 样本个数
1.4 损失函数是 ℓ 0 / 1 \ell_{0/1} ℓ0/1的软间隔SVM最优化问题
ℓ 0 / 1 \ell_{0/1} ℓ0/1损失函数:满足1,2特点
只能判断样本是否满足约束
- z = y i ( w ⃗ T x ⃗ + b ) − 1 z = y_i(\vec{w}^T\vec{x}+b)-1 z=yi(wTx+b)−1
- 满足约束条件的样本: z ≥ 0 z \ge 0 z≥0,则损失=0
- 不满足约束条件的样本: z < 0 z < 0 z<0,则损失=1
软间隔SVM最优化问题变为
- C是>0的常数,用于调节损失函数的权重。
- 当我们允许较多样本不满足约束条件时,可以让C小一点,即损失的权重小一点。
- 反之允许较少样本不满足约束条件,就让C大一点。
- 特殊的:即硬间隔的情况,我们不允许任何样本不满足约束条件,则让 C → + ∞ C \to +\infin C→+∞,让损失函数权重无穷大,你必须让所有样本的损失 = 0
- 因此该式子可以看成 SVM的一般形式
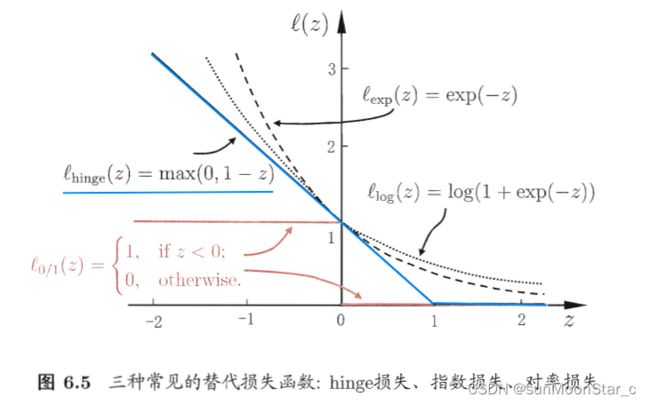
1.4 替代损失(surrogate loss)函数: ℓ h i n g e = max { 0 , 1 − z } \ell_{hinge}=\max\{0,1-z\} ℓhinge=max{0,1−z}合页损失:满足特点3
ℓ 0 / 1 \ell_{0/1} ℓ0/1损失函数:非凸,非连续,数学性质不好
替代损失函数 一般有较好的数学性质:
- 通常是凸的连续函数
- 可以表示不满足约束的程度
常见替代损失函数图像
- ℓ h i n g e ≥ 0 \ell_{hinge} \ge 0 ℓhinge≥0
- 满足特点3:损失和违反约束条件的程度成正比
则软间隔SVM最优化问题变为:
1.5 引入松弛变量(slack variables) ξ i \xi_i ξi:样本不满足约束的程度
对松弛变量的2个约束

令 ξ i = ℓ h i n g e ( z ) = m a x ( 0 , 1 − y i ( w ⃗ T x ⃗ i ) + b ) \xi_i = \ell_{hinge}(z) = max(0,1-y_i(\vec{w}^T\vec{x}_i)+b) ξi=ℓhinge(z)=max(0,1−yi(wTxi)+b)
约束1: ξ i ≥ 0 \xi_i\ge 0 ξi≥0
约束2: y i ( w ⃗ T x ⃗ i ) + b ≥ 1 − ξ i y_i(\vec{w}^T\vec{x}_i)+b \ge 1-\xi_i yi(wTxi)+b≥1−ξi
- 1 − y i ( w ⃗ T x ⃗ i ) + b ) ≥ 0 1-y_i(\vec{w}^T\vec{x}_i)+b) \ge 0 1−yi(wTxi)+b)≥0时, ξ i = 1 − y i ( w ⃗ T x ⃗ i ) + b \xi_i = 1-y_i(\vec{w}^T\vec{x}_i)+b ξi=1−yi(wTxi)+b
- 1 − y i ( w ⃗ T x ⃗ i ) + b ) < 0 1-y_i(\vec{w}^T\vec{x}_i)+b) < 0 1−yi(wTxi)+b)<0时, ξ i = 0 > 1 − y i ( w ⃗ T x ⃗ i ) + b \xi_i = 0 >1-y_i(\vec{w}^T\vec{x}_i)+b ξi=0>1−yi(wTxi)+b
- 因此 ξ i ≥ 1 − y i ( w ⃗ T x ⃗ i ) + b \xi_i \ge 1-y_i(\vec{w}^T\vec{x}_i)+b ξi≥1−yi(wTxi)+b,即 y i ( w ⃗ T x ⃗ i ) + b ≥ 1 − ξ i y_i(\vec{w}^T\vec{x}_i)+b \ge 1-\xi_i yi(wTxi)+b≥1−ξi
软间隔SVM最优化问题变为
- m个样本各对应一个松弛变量,表示样本不满足原问题约束 y i ( w ⃗ T x ⃗ + b ) ≥ 1 y_i(\vec{w}^T\vec{x}+b) \ge 1 yi(wTx+b)≥1的程度
- 与原问题6.6一样,仍然是二次规划问题
1.6 软间隔SVM问题 转化为对偶问题
具体如何转化为对偶问题求最优解详情见SVM笔记
2、求对偶函数 inf L \inf L infL,即求L的最小值,L是凸优化问题,求偏导=0
3、得到软间隔下SVM问题的对偶问题:
- 两个拉格朗日乘子都>=0构成约束: 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C
- 硬间隔SVM问题的不等式约束只有1个,没有对松弛变量 ξ i \xi_i ξi的约束,则其拉格朗日问题自然少参数,约束只有 α i ≥ 0 \alpha_i \ge 0 αi≥0
KKT条件
依然参见SVM笔记
1.7 求解对偶问题6.40(暂时不讲)
和硬间隔中求解方法一样,暂时不讲。
二、支持向量回归SVR(support vector regression)
2.1 背景
这里的总结个人感觉比SVM部分清晰点了。
SVM讨论的是分类问题,希望学得一个能实现分类的,最大间隔的超平面模型 f ( x ⃗ ) = w ⃗ T x ⃗ + b f(\vec{x}) = \vec{w}^T\vec{x}+b f(x)=wTx+b:
- 实现分类:回归模型 w ⃗ T x ⃗ + b \vec{w}^T\vec{x}+b wTx+b套上sign函数实现分类。
- 如果是软间隔SVM问题,数据集线性不可分,则最优化问题:既要最大间隔,也要样本不满足约束条件的程度(hinge损失函数)最小化。
- 如果是硬间隔SVM问题,代表数据集线性可分,不存在不满足约束条件的样本。则最优化问题只需要间隔最大化即可。
SVR讨论的是回归问题:希望学得一个回归模型 f ( x ⃗ ) = w ⃗ T x ⃗ + b f(\vec{x}) = \vec{w}^T\vec{x}+b f(x)=wTx+b,使得预测值 f ( x ⃗ ) f(\vec{x}) f(x)和真实标记 y y y尽可能接近。
传统的回归模型:预测值 f ( x ⃗ ) f(\vec{x}) f(x)和真实标记 y y y完全相同,才算没有损失。【这里损失都是均方误差】
SVR模型:能容忍预测值 f ( x ⃗ ) f(\vec{x}) f(x)和真实标记 y y y最多 ϵ \epsilon ϵ的偏差,该偏差内,都算没有损失,预测正确。
即线性回归模型,变成带状回归模型了。
我们要尽可能使得这个间隔带 从样本的最密集地带(中心)穿过,达到拟合训练样本效果。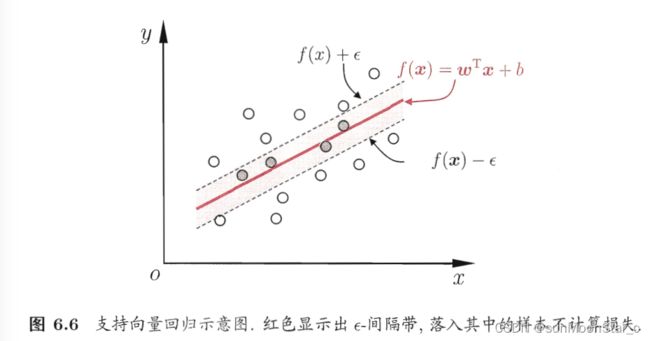
2.2、SVR最优化问题:正则项+损失函数 ℓ ϵ \ell_\epsilon ℓϵ
保证形式和SVM软间隔问题一模一样
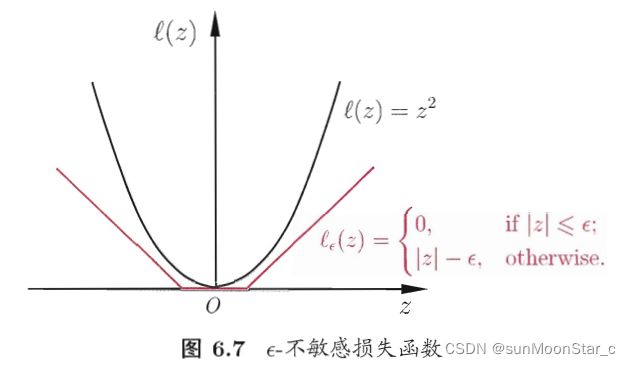
1、 ℓ ϵ \ell_\epsilon ℓϵ不敏感损失函数:性质好
ℓ ϵ \ell_\epsilon ℓϵ不敏感损失函数,比均方误差少个平方项。
- 不写成均方误差,是为了和软间隔SVM最优化问题形式保持一致
- 该损失函数自身性质已经很好,如图:是连续的凸函数,能表示拟合程度,不需要替代函数了
2、正则项
前面的 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 {1\over 2}||\vec{w}||^2 21∣∣w∣∣2不能理解为SVM中的间隔最大化了。
- 这里的 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 {1\over 2}||\vec{w}||^2 21∣∣w∣∣2叫做 L 2 L_2 L2正则项,能防止过拟合;(正则化本身作用,这里暂时不讲)
- 该正则项也是为了和软间隔SVM的最优化问题形式保持一致。
和软间隔SVM的最优化问题形式保持一致,则可以引入松弛变量,通过对偶问题求解,使用核函数等等SVM可用的方法。
2.3 引入松弛变量 ξ i = ℓ ϵ ( z ) = ℓ ϵ ( f ( x ⃗ i ) − y i ) \xi_i = \ell_\epsilon(z) = \ell_\epsilon(f(\vec{x}_i)-y_i) ξi=ℓϵ(z)=ℓϵ(f(xi)−yi)
松弛变量的2个约束条件
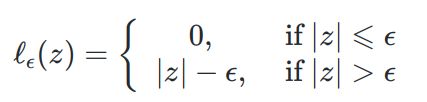
ξ i = ℓ ϵ ( z ) \xi_i = \ell_\epsilon(z) ξi=ℓϵ(z)
约束1: ξ i ≥ 0 \xi_i \ge 0 ξi≥0(即损失函数取值>=0)
SVR最优化问题转化为
两边采用不同松弛程度: ξ i , ξ i ^ \xi_i, \hat{\xi_i} ξi,ξi^的SVR最优化问题
这样更合理,因为如果样本在SVR间隔带模型的上面,则:f - y必然是个负数,右边必然成立, ξ i \xi_i ξi直接令其=0,不用考虑后面求解了。
如果样本在SVR间隔带模型的下面,同理,左边不用考虑,令 ξ i ^ = 0 \hat{\xi_i} = 0 ξi^=0。
2.4 转化为对偶问题
和SVM问题形式一模一样,自然求解方法也都可以用一样的
2、拉格朗日函数:有4个不等式约束条件,需要4个拉格朗日乘子

3、求对偶函数,即求拉格朗日函数最小值:L是凸优化问题,求偏导=0即可
4、得到对偶问题
约束条件用两个拉格朗日乘子表示
一个是6.48
一个是乘子都要>=0,根据6.49,6.50 推出来

5、上述问题要满足KKT条件