Attention机制详解
一、Attention 原理
在Encoder-Decoder结构中,Encoder把所有的输入序列都编码成一个统一的语义特征c再解码,因此, c中必须包含原始序列中的所有信息,它的长度就成了限制模型性能的瓶颈。如机器翻译问题,当要翻译的句子较长时,一个c可能存不下那么多信息,就会造成翻译精度的下降。
相比于原始的Seq2Seq模型的Decoder中只通过同一个向量c去计算隐状态,Attention在Decoder部分的每个时间输入不同的c来解决这个问题,这就是它最核心的创新。下图是带有Attention机制的Decoder:
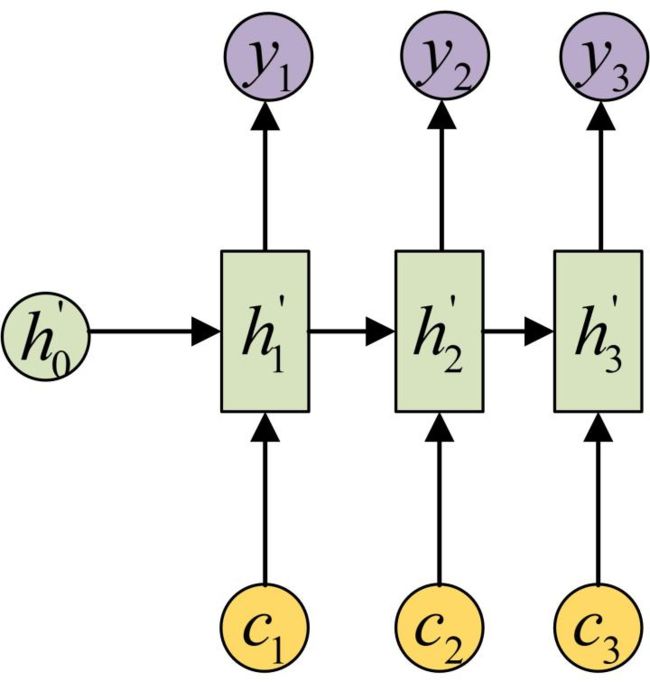
看一下最开始的Attention模型架构如下:
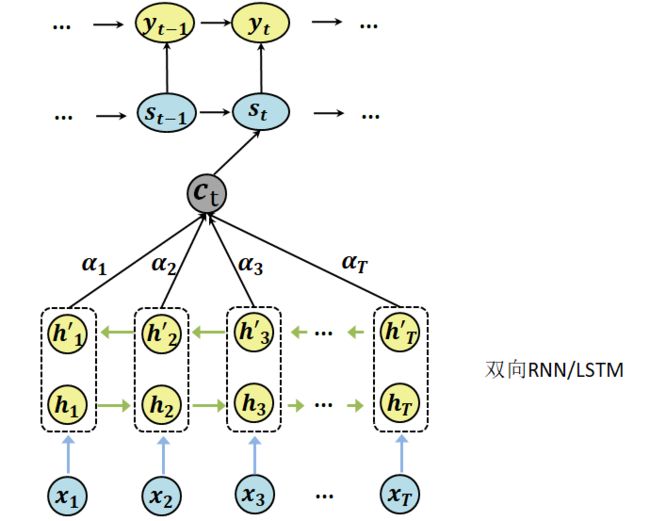
- 输入: ( x 1 , x 2 , . . . , x M ) (x_1, x_2,...,x_M) (x1,x2,...,xM)序列是待翻译的句子。
- Encoder:双向的RNN或LSTM,计算得到每个位置的隐状态,下面用 h i h_i hi表示。
- Decoder:对当前输出位置 t,使用Decoder中上一个隐状态 s t − 1 s_{t-1} st−1与Encoder的结果(也就是向量 c t c_t ct)计算t位置的对应的 y t y_t yt。
- 输出: ( y 1 , y 2 , . . . , y T ) (y_1,y_2,...,y_T) (y1,y2,...,yT)序列是翻译之后的句子。
来详细看一下每一个位置的输出 y t y_t yt 是怎么计算得到的:
(1)先来看看当前t位置的上下文向量 c t c_t ct是怎么计算得到的,其实 c t c_t ct是由Encoder部分所有的隐状态 h m h_{m} hm和对应的权重 α t m \alpha_{tm} αtm加权求和得到的:
c t = ∑ m = 1 M α t m h m c_t=\sum_{m=1}^{M} \alpha_{tm}h_m ct=m=1∑Mαtmhm
这里这个权重 α t m \alpha_{tm} αtm 是用来衡量Encoder中位置m的 h m h_m hm 对Decoder中当前t位置的状态 s t s_t st的影响,也就是 h m h_m hm 和 s t s_t st的相关性。那么这些权重 α t m \alpha_{tm} αtm是怎么得到的呢?事实上, α t m \alpha_{tm} αtm和Decoder的第 t-1 阶段的隐状态 s t − 1 s_{t-1} st−1(也有一些模型中直接使用当前状态 s t s_t st:下面的Global Attention)、Encoder第m个阶段的隐状态 h m h_m hm 有关。可以表示为:
e t m = ψ ( s t − 1 , h m ) , α t m = e x p ( e t m ) ∑ j = 1 M e x p ( e t j ) e_{tm}=\psi(s_{t-1}, h_m),\: \alpha_{tm}=\frac{exp(e_{tm})}{\sum_{j=1}^{M} exp(e_{tj})} etm=ψ(st−1,hm),αtm=∑j=1Mexp(etj)exp(etm)
其实这个 e t m e_{tm} etm 就是我们上面提到的 h m h_m hm 和 s t s_t st 的相关性(对齐程度),而后面的 α t m \alpha_{tm} αtm则对 e t m e_{tm} etm进行softmax将其normalization得到attention权重分布,概率值的和为1。
对齐模型 e t m e_{tm} etm 的计算方式(也就是上面那个 ψ \psi ψ函数)有很多种,不同的计算方式,代表不同的Attention模型,最简单且最常用的的对齐模型是dot product乘积矩阵,即把target端的输出隐状态与source端的输出隐状态进行矩阵乘。常见的对齐计算方式如下:
- 点乘形式: e t m = s t − 1 T ⋅ h m e_{tm}=s_{t-1}^T \cdot h_m etm=st−1T⋅hm
- 加权点乘: e t m = s t − 1 T ⋅ W ⋅ h m e_{tm}=s_{t-1}^T \cdot W \cdot h_m etm=st−1T⋅W⋅hm
- concat映射: e t m = v a T t a n h ( W [ s t − 1 ; h m ] ) e_{tm}=v_a^T \ tanh(W[s_{t-1};h_m]) etm=vaT tanh(W[st−1;hm])
(3)然后,使用上一个隐状态 s t − 1 s_{t-1} st−1、上一个输出 y t − 1 y_{t-1} yt−1、当前位置的上下文向量 c t c_t ct更新当前隐状态:
s t = f ( s t − 1 , y t − 1 , c t ) s_t=f(s_{t-1}, y_{t-1}, c_t) st=f(st−1,yt−1,ct)
(4)根据当前隐状态 s t s_{t} st、上一个输出 y t − 1 y_{t-1} yt−1、当前位置的上下文向量 c t c_t ct计算当前输出 y t y_t yt:
y t = g ( s t , y t − 1 , c t ) y_t=g(s_{t}, y_{t-1}, c_t) yt=g(st,yt−1,ct)
通过为每个输出位置计算一个context vector,使得每个位置的输出可以关注到输入中最相关的部分,也就是所说的“注意力”,因此效果比传统模型更好。
二、Attention 分类
2.1 Soft Attention 和 Hard Attention
Kelvin Xu等人2015年发表的论文《Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》中,同时引入了Soft Attention和Hard Attention。我们之前所描述的传统的Attention Mechanism就是Soft Attention。
Soft Attention计算得到的对齐向量 α \alpha α是一个概率分布,总和为1。Soft Attention是参数化的(Parameterization),因此可导,可以被嵌入到模型中去,直接训练。梯度可以经过Attention Mechanism模块,反向传播到模型其他部分。原始的Attention就是Soft Attention。
相反,Hard Attention是一个随机的过程。Hard Attention不会选择整个encoder的输出做为其输入,Hard Attention会依概率Si来采样输入端的隐状态一部分来进行计算,而不是整个encoder的隐状态。为了实现梯度的反向传播,需要采用蒙特卡洛采样的方法来估计模块的梯度。Hard Attention对每个位置计算对齐概率,但只将最高的一个置为1,其余置为0。
两种Attention Mechanism都有各自的优势,但目前更多的研究和应用还是更倾向于使用Soft Attention,因为其可以直接求导,进行梯度反向传播。
2.2 Global Attention 和 Local Attention
Global Attention:和原始的Attention模型一样。所有的hidden state都被用于计算Context vector 的权重,即变长的对齐向量 α t \alpha_t αt,其长度等于encoder端输入句子的长度。但是原始的Attention模型中的对齐向量 α t m \alpha_{tm} αtm和Decoder的第 t-1 阶段的隐状态 s t − 1 s_{t-1} st−1、Encoder第m个阶段的隐状态 h m h_m hm 有关,而Global Attention的对齐向量 α t m \alpha_{tm} αtm和Decoder的当前t位置状态 s t s_t st、Encoder第m个阶段的隐状态 h m h_m hm 有关。
Local Attention:Global Attention有一个明显的缺点就是,每一次,encoder端的所有hidden state都要参与计算向量c,这样做计算开销会比较大,特别是当encoder的句子偏长,比如,一段话或者一篇文章,效率偏低。因此,为了提高效率,Local Attention应运而生。
Local Attention是一种介于Kelvin Xu所提出的Soft Attention和Hard Attention之间的一种Attention方式,即把两种方式结合起来。其结构如下图所示:
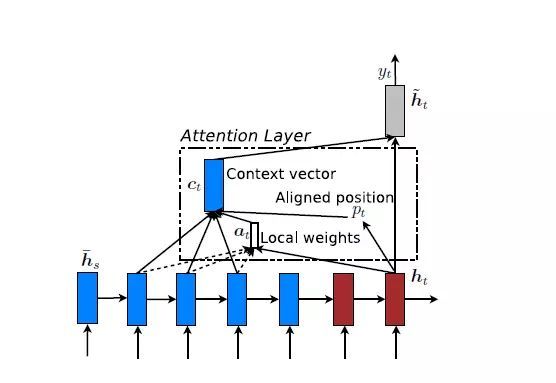
Local Attention首先会为decoder端当前的词,预测一个source端对齐位置(aligned position) p t p_t pt,然后基于 p t p_t pt选择一个窗口,也就是只关注一部分encoder hidden states,用于计算上下文向量 c t c_t ct。 p t p_t pt的计算公式如下:
p t = S ⋅ s i g m o i d ( v p T t a n h ( W p h t ) ) p_t=S \cdot sigmoid(v_p^T \ tanh(W_ph_t)) pt=S⋅sigmoid(vpT tanh(Wpht))
其中,S是encoder端句子长度, v p v_p vp 和 W p W_p Wp 是模型参数。此时,对齐向量 α t \alpha_t αt 的计算公式如下:
α t = a l i g n ( h t , h ~ t ) e x p ( − ( s − p t ) 2 2 σ 2 ) \alpha_t=align(h_t,\tilde h_t)exp(-\frac{(s-p_t)^2}{2 \sigma^2}) αt=align(ht,h~t)exp(−2σ2(s−pt)2)
总之,Global Attention和Local Attention各有优劣,在实际应用中,Global Attention应用更普遍,因为local Attention需要预测一个位置向量p,这就带来两个问题:
- 当encoder句子不是很长时,相对Global Attention,计算量并没有明显减小。
- 位置向量pt的预测并不非常准确,这就直接计算的到的local Attention的准确率。
2.3 Self Attention
《Attention is all you nedd》中提出的一种Attention模型,详见:Transformer 模型详解。它反应的是输入或者输出的序列内部的单词和单词之间的相互影响。
2.4 Hierarchical Attention
Zichao Yang等人在论文《Hierarchical Attention Networks for Document Classification》提出了Hierarchical Attention用于文档分类。Hierarchical Attention构建了两个层次的Attention Mechanism,第一个层次是对句子中每个词的attention,即word attention;第二个层次是针对文档中每个句子的attention,即sentence attention。结构图如下:
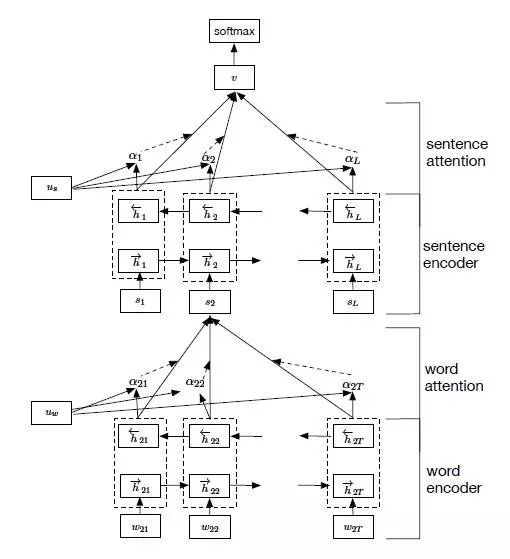
整个网络结构由四个部分组成:一个由双向RNN(GRU)构成的word sequenceencoder,然后是一个关于词的word-level的attention layer;基于word attention layar之上,是一个由双向RNN构成的sentence encoder,最后的输出层是一个sentence-level的attention layer。
2.5 Attention over Attention
科大讯飞和哈工大在2017ACL会议上的论文《Attention-over-Attention Neural Networks for Reading Comprehension》中提出了Attention Over Attention的Attention机制,计算的是问题(Query)中的每个单词对文档(Document)中某个单词的重要程度(即注意力)。结构如下图所示:
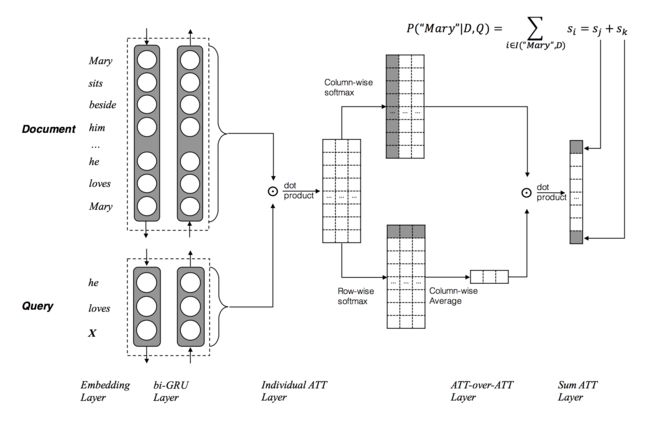
两个输入,一个Document和一个Query,分别用一个双向的RNN进行特征抽取,得到各自的隐状态h(doc)和h(query),然后基于query和doc的隐状态进行dot product,得到query和doc的attention关联矩阵。
- 按列进行计算,得到
文档中每个单词对问题中的某个单词的重要程度(即注意力),最后形成一个文档级别的注意力分布 α ( t ) \alpha(t) α(t)。问题中有多少个单词就有多少个这样的分布。然后对所有的 α ( t ) \alpha(t) α(t)进行汇总(求和、平均值或者最大值):
α ( t ) = s o f t m a x ( M ( 1 , t ) , M ( 2 , t ) , . . . , M ( P , t ) ) \alpha(t)=softmax(M(1,t),M(2,t),...,M(P,t)) α(t)=softmax(M(1,t),M(2,t),...,M(P,t)),P是文档中单词的个数
A = [ α ( 1 ) , α ( 2 ) , . . . , α ( Q ) ] \Alpha=[\alpha(1),\alpha(2),...,\alpha(Q)] A=[α(1),α(2),...,α(Q)],Q是问题中单词个数 - 按行进行计算,得到
问题中的每个单词对文档中某个单词的重要程度(即注意力),形成一个问题级别的注意力分布 β ( t ) \beta(t) β(t)。文档中有多少个单词就有多少个这样的分布。然后对这些分布进行累加并求平均得到 B \Beta B:
β ( t ) = s o f t m a x ( M ( t , 1 ) , M ( t , 2 ) , . . . , M ( t , Q ) \beta(t)=softmax(M(t,1),M(t,2),...,M(t,Q) β(t)=softmax(M(t,1),M(t,2),...,M(t,Q),Q是问题中单词个数
B = 1 P ∑ t = 1 P β ( t ) \Beta=\frac{1}{P} \sum_{t=1}^{P} \beta(t) B=P1∑t=1Pβ(t) ,P是文档中单词的个数
2.6 Multi-step Attention
2017年,FaceBook 人工智能实验室的Jonas Gehring等人在论文《Convolutional Sequence to Sequence Learning》提出了完全基于CNN来构建Seq2Seq模型,除了这一最大的特色之外,论文中还采用了多层Attention Mechanism,来获取encoder和decoder中输入句子之间的关系,结构如下图所示:
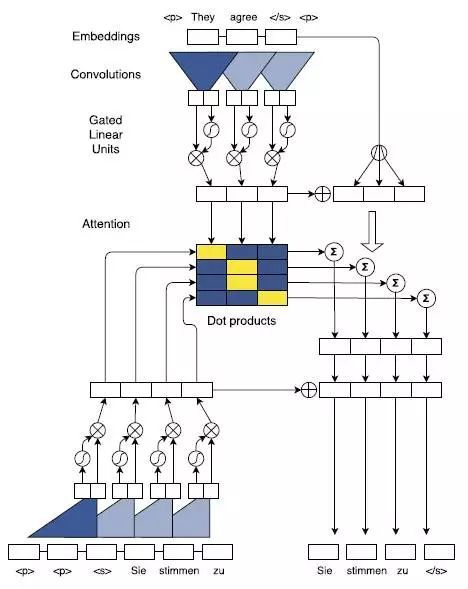
完全基于CNN的Seq2Seq模型需要通过层叠多层来获取输入句子中词与词之间的依赖关系,特别是当句子非常长的时候,我曾经实验证明,层叠的层数往往达到10层以上才能取得比较理想的结果。针对每一个卷积的step(输入一个词)都对encoder的hidden state和decoder的hidden state进行dot product计算得到最终的Attention 矩阵,并且基于最终的attention矩阵去指导decoder的解码操作。
2.7 Multi-dimensional Attention
传统的Attention往往是一维的。《Coupled Multi-Layer Attentions for Co-Extraction of Aspect and Opinion Terms》提出了Multi-dimensional attention把一维的Attention扩展到多维,多维Attention可以捕捉输入多个维度重要性,具有更强的描述能力。
2.8 Memory-based Attention
Memory机制在NLP中应用也比较广泛,比如对话系统中。Memory-based Attention借用了这一思想,假设输入为q,Memory中以(k,v)形式存储着我们需要的上下文。Memory-based Attention可以通过不停地迭代地更新Memory来将注意力转移到答案所在的位置。
参考:
【1】 模型汇总24 - 深度学习中Attention Mechanism详细介绍:原理、分类及应用
【2】干货|全面了解attention机制
【3】干货 | Attention注意力机制超全综述
【4】 Seq2Seq – Attention – Transformer