机器学习【一】————线性回归方法处理非线性数据
线性回归方法处理非线性数据
- 任务目标:
- 代码内容:
- 代码解析:
-
-
- 1.读取excel表格数据
- 2.拟合线性函数
- 3.拟合非线性函数
- 4.对结果进行评估
-
- 总结:
任务目标:
前言:这周学习了用线性回归的方式处理,这是第一次运用,目前能了解线性回归的用法,但仍然不够深入,如果有看见了文章里有一些错误或疑惑的地方还请指出!欢迎大家评论区留言或私信。
对excel表格数据进行提取,并用线性回归方式,求解非线性回归问题
代码内容:
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
data = pd.read_csv('data_nonlinear.csv')
data.head()
x = data.loc[:,'x']
y = data.loc[:,'y']
fig1 = plt.figure(figsize=(5,5))
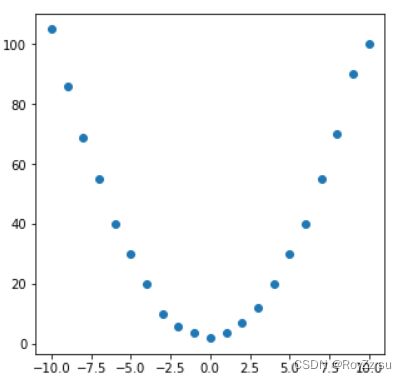
plt.scatter(x,y)
plt.show()
x = np.array(x).reshape(-1,1)
from sklearn.linear_model import LinearRegression
LR = LinearRegression()
LR.fit(x,y)
y_predict = LR.predict(x)
fig2 = plt.figure(figsize=(5,5))
plt.scatter(x,y)
plt.plot(x,y_predict,'r')
plt.show()
x2 = x*x
x_new = np.append(x,x2,axis=1)
LR2 = LinearRegression()
LR2.fit(x_new,y)
y_new_predict = LR2.predict(x_new)
fig3 = plt.figure(figsize=(5,5))
plt.scatter(x,y)
plt.scatter(x,y_new_predict)
plt.show()
from sklearn.metrics import mean_squared_error,r2_score
mean_squared_error_l = mean_squared_error(y,y_new_predict)
r2_score_l = r2_score(y,y_new_predict)
mean_squared_error_l,r2_score_l
代码解析:
这里是我作为一个初学者的理解,并不一定理解正确,如果有误或有更好解释的欢迎留言指出!
1.读取excel表格数据
data = pd.read_csv('data_nonlinear.csv')
data.head() #读数据
x = data.loc[:,'x'] #索引找到数据
y = data.loc[:,'y']
fig1 = plt.figure(figsize=(5,5)) #建立5*5表格
plt.scatter(x,y) #画散点图
plt.show() #展示散点图
使用pandas库函数将表格数据存在data中,并且通过索引找到数据的x和y(这里表格中只有xy两个一一对应的数据,多因子需要改变x的列表使其检索多个),figure函数可以规定表格的大小,数据点大小颜色和形状等等。
2.拟合线性函数
from sklearn.linear_model import LinearRegression
LR = LinearRegression() #建立模型
LR.fit(x,y) #用xy关系建立LR模型
y_predict = LR.predict(x) #输出新数据
fig2 = plt.figure(figsize=(5,5))
plt.scatter(x,y)
plt.plot(x,y_predict,'r') #画出y_predict和x的图,颜色为红
plt.show()
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合(自变量都是一次方)。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。(百度百科)
fit() 用来分析模型参数,predict() 是通过 fit() 算出的模型参数构成的模型,对解释变量进行预测获得的值。所以LR = LinearRegression()可以理解为LR建立一个LinearRegression模型,然后用建立好的LR分析xy的关系,也就是LR.fit(x,y)。这时LR就是一个新模型,这个模型就是用x和y建立的模型
LR -> y = kx + b
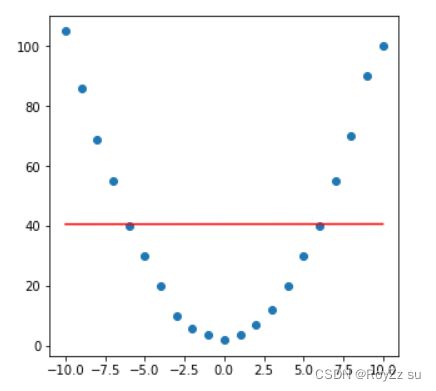
y_predict = LR.predict(x),就是在已经建立的LR模型中输入x,输出对应的y_predict。我们将x和y_predict画出(图中红线)。
- 线性拟合
3.拟合非线性函数
x2 = x*x
x_new = np.append(x,x2,axis=1)
LR2 = LinearRegression()
LR2.fit(x_new,y)
y_new_predict = LR2.predict(x_new)
fig3 = plt.figure(figsize=(5,5))
plt.scatter(x,y)
plt.scatter(x,y_new_predict)
plt.show()
根据表格数据我们可以看出数据近似平方关系,于是我们建立一个二次函数模型。这里先把x2,也就是x的平方,与x组成一个二维数组x_new,然后对x_new与y进行训练。
这里我的理解是:在第一个单因子模型的建立中,假设x=-10时,y=100。x=0时,y=0。x=10时y=100,所以建立的模型对应下来就类似一个一次函数。
而第二个多因子模型,假设x=-10,x2=100时,y=100。x=-9,x2=81时,y=81。x=0,x2=0时y=0。x=10,x2=100时,y=100。所以对应下来y的位置更接近于x2的位置,而不是只对应x2.
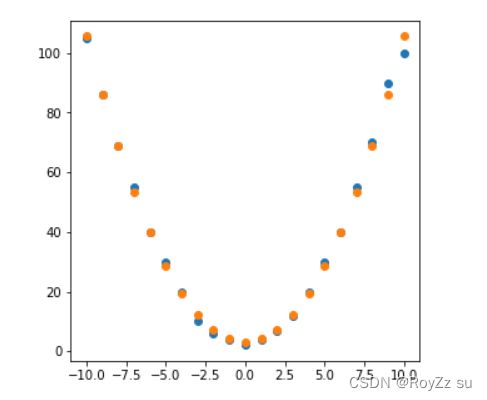
建立模型后画出散点图
- 非线性拟合
4.对结果进行评估
from sklearn.metrics import mean_squared_error,r2_score
mean_squared_error_l = mean_squared_error(y,y_new_predict) #均方差
r2_score_l = r2_score(y,y_new_predict) #决定系数R2
mean_squared_error_l,r2_score_l
这里就是算出了均方差和决定系数R2的值来评估刚刚拟合的效果
- 拟合效果(均方差,决定系数)
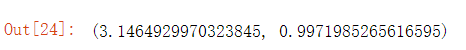
可以看出决定系数为0.997,非常接近1,可以下结论拟合效果好
总结:
线性回归方法是机器学习入门级的方法,本人学识尚浅,理解不足,若有看见文章中有不足或错误的地方欢迎提出!大家一起学习进步。