Self-Attention和Multi-Head Attention的详细代码内容(没有原理)
先看self-attention
(原理可以参考这个:层层剖析,让你彻底搞懂Self-Attention、MultiHead-Attention和Masked-Attention的机制和原理_iioSnail的博客-CSDN博客_attention mask)
class SelfAttention(nn.Module):
def __init__(self, input_vector_dim: int, dim_k=None, dim_v=None):
"""
初始化SelfAttention,包含如下关键参数:
input_vector_dim: 输入向量的维度,对应上述公式中的d,例如你将单词编码为了10维的向量,则该值为10
dim_k: 矩阵W^k和W^q的维度
dim_v: 输出向量的维度,即b的维度,例如如果想让Attention后的输出向量b的维度为15,则定义为15,若不填,默认取取input_vector_dim
"""
super(SelfAttention, self).__init__()
self.input_vector_dim = input_vector_dim
# 如果 dim_k 和 dim_v 为 None,则取输入向量的维度
if dim_k is None:
dim_k = input_vector_dim
if dim_v is None:
dim_v = input_vector_dim
"""
实际写代码时,常用线性层来表示需要训练的矩阵,方便反向传播和参数更新
"""
self.W_q = nn.Linear(input_vector_dim, dim_k, bias=False)
self.W_k = nn.Linear(input_vector_dim, dim_k, bias=False)
self.W_v = nn.Linear(input_vector_dim, dim_v, bias=False)
# 这个是根号下d_k
self._norm_fact = 1 / np.sqrt(dim_k)
def forward(self, x):
"""
进行前向传播:
x: 输入向量,size为(batch_size, input_num, input_vector_dim)
"""
# 通过W_q, W_k, W_v矩阵计算出,Q,K,V
# Q,K,V矩阵的size为 (batch_size, input_num, output_vector_dim)
Q = self.W_q(x)
K = self.W_k(x)
V = self.W_v(x)
# permute用于变换矩阵的size中对应元素的位置,
# 即,将K的size由(batch_size, input_num, output_vector_dim),变为(batch_size, output_vector_dim,input_num)
# 0,1,2 代表各个元素的下标,即变换前,batch_size所在的位置是0,input_num所在的位置是1
K_T = K.permute(0, 2, 1)
# bmm是batch matrix-matrix product,即对一批矩阵进行矩阵相乘
# bmm详情参见:https://pytorch.org/docs/stable/generated/torch.bmm.html
atten = nn.Softmax(dim=-1)(torch.bmm(Q, K_T)) * self._norm_fact
# 最后再乘以 V
output = torch.bmm(atten, V)
return output再看Multi-Head Attention
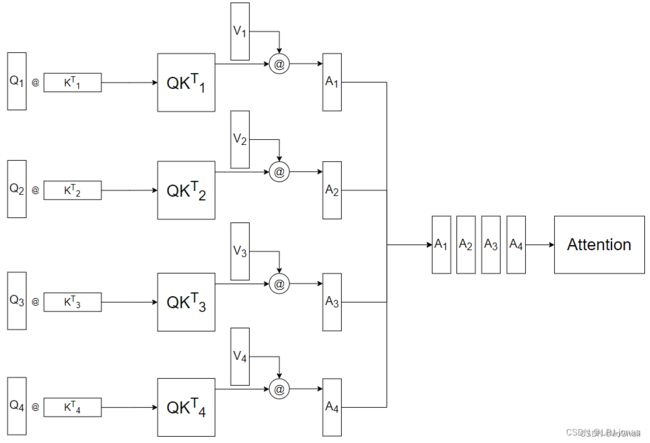
MultiHead Attention在带入公式前做了一件事情,就是拆,它按照“词向量维度”这个方向,将Q,K,V拆成了多个头,如图所示:
注意力计算机制与self-attention类似,但该方法会在词向量维度方向将Q、K、V分割成多个“head”,分别计算后再拼在一起。由于性能降低,需要再采用一个额外的Wo矩阵,对Attention再进行一次线性变换。
def attention(query, key, value):
"""
计算Attention的结果。
这里其实传入的是Q,K,V,而Q,K,V的计算是放在模型中的,请参考后续的MultiHeadedAttention类。
这里的Q,K,V有两种Shape,如果是Self-Attention,Shape为(batch, 词数, d_model),
例如(1, 7, 128),即batch_size为1,一句7个单词,每个单词128维
但如果是Multi-Head Attention,则Shape为(batch, head数, 词数,d_model/head数),
例如(1, 8, 7, 16),即Batch_size为1,8个head,一句7个单词,128/8=16。
这样其实也能看出来,所谓的MultiHead其实就是将128拆开了。
在Transformer中,由于使用的是MultiHead Attention,所以Q,K,V的Shape只会是第二种。
"""
# 获取d_model的值。之所以这样可以获取,是因为query和输入的shape相同,
# 若为Self-Attention,则最后一维都是词向量的维度,也就是d_model的值。
# 若为MultiHead Attention,则最后一维是 d_model / h,h为head数
d_k = query.size(-1)
# 执行QK^T / √d_k
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
# 执行公式中的Softmax
# 这里的p_attn是一个方阵
# 若是Self Attention,则shape为(batch, 词数, 次数),例如(1, 7, 7)
# 若是MultiHead Attention,则shape为(batch, head数, 词数,词数)
p_attn = scores.softmax(dim=-1)
# 最后再乘以 V。
# 对于Self Attention来说,结果Shape为(batch, 词数, d_model),这也就是最终的结果了。
# 但对于MultiHead Attention来说,结果Shape为(batch, head数, 词数,d_model/head数)
# 而这不是最终结果,后续还要将head合并,变为(batch, 词数, d_model)。不过这是MultiHeadAttention
# 该做的事情。
return torch.matmul(p_attn, value)
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model):
"""
h: head的数量
"""
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
# 定义W^q, W^k, W^v和W^o矩阵。
# 如果你不知道为什么用nn.Linear定义矩阵,可以参考该文章:
# https://blog.csdn.net/zhaohongfei_358/article/details/122797190
self.linears = [
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
nn.Linear(d_model, d_model),
]
def forward(self, x):
# 获取Batch Size
nbatches = x.size(0)
"""
1. 求出Q, K, V,这里是求MultiHead的Q,K,V,所以Shape为(batch, head数, 词数,d_model/head数)
1.1 首先,通过定义的W^q,W^k,W^v求出SelfAttention的Q,K,V,此时Q,K,V的Shape为(batch, 词数, d_model)
对应代码为 `linear(x)`
1.2 分成多头,即将Shape由(batch, 词数, d_model)变为(batch, 词数, head数,d_model/head数)。
对应代码为 `view(nbatches, -1, self.h, self.d_k)`
1.3 最终交换“词数”和“head数”这两个维度,将head数放在前面,最终shape变为(batch, head数, 词数,d_model/head数)。
对应代码为 `transpose(1, 2)`
"""
query, key, value = [
linear(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for linear, x in zip(self.linears, (x, x, x))
]
"""
2. 求出Q,K,V后,通过attention函数计算出Attention结果,
这里x的shape为(batch, head数, 词数,d_model/head数)
self.attn的shape为(batch, head数, 词数,词数)
"""
x = attention(
query, key, value
)
"""
3. 将多个head再合并起来,即将x的shape由(batch, head数, 词数,d_model/head数)
再变为 (batch, 词数,d_model)
3.1 首先,交换“head数”和“词数”,这两个维度,结果为(batch, 词数, head数, d_model/head数)
对应代码为:`x.transpose(1, 2).contiguous()`
3.2 然后将“head数”和“d_model/head数”这两个维度合并,结果为(batch, 词数,d_model)
"""
x = (
x.transpose(1, 2)
.contiguous()
.view(nbatches, -1, self.h * self.d_k)
)
# 最终通过W^o矩阵再执行一次线性变换,得到最终结果。
return self.linears[-1](x)