数值计算大作业：Jacobi与Gauss -Seidel迭代求解线性方程组（Matlab实现）

作为研究生的入门课，数值计算的大作业算是所有研究生开学的重要编程作业。

    我把Jacobi与Gauss -Seidel迭代求解线性方程组的数值计算作业在MATLAB中编程实现。具体的程序详细标注后放在文章附录了，需要的同学自取。下文为作业详解

Jacobi解方程数学原理：

考虑线性方程组Ax = b时，一般当A为低阶稠密矩阵时，用主元消去法解此方程组是有效方法。但是，对于由工程技术中产生的大型稀疏矩阵方程组（A的阶数很高，但零元素较多，例如求某些偏微分方程数值解所产生的线性方程组），利用迭代法求解此方程组就是合适的，在计算机内存和运算两方面，迭代法通常都可利用A中有大量零元素的特点。

   首先将方程组中的系数矩阵A分解成三部分，即：A=L+D+U，其中D为对角阵，L为下三角矩阵，U为上三角矩阵。之后确定迭代格式，X^(k+1)=J*X^(k)+f ，（这里^表示的是上标，括号内数字即迭代次数），雅克比迭代法中一般记为J。（k=0,1，......）再选取初始迭代向量X^(0)，开始逐次迭代

   并非所以矩阵都可以使用雅各比迭代的，设Ax= b，其中A=D+L+U为非奇异矩阵，且对角阵D也非奇异，则当迭代矩阵J的谱半径ρ（J）<1时，雅克比迭代法收敛。

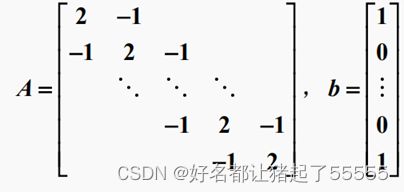
题目：给定n阶线性方程组Ax=b，其中

 完成以下工作：

1.当n=10,20,50,100,200时，使用Jacobi迭代求解上述线性方程组，输出Jacobi迭代法迭代精度达到10^(-8)时的迭代次数及迭代矩阵的谱半径与方程组阶数n的关系。

本题利用雅克比迭代运算结果如下表所示

n	迭代次数	误差	迭代矩阵的谱半径
10	396	7.8454*10^(-9)	3.3190
20	1367	6.0772*10^(-9)	3.9777
50	7383	3.9476*10^(-9)	3.9962
100	26848	2.8117*10^(-9)	3.9990
200	97889	1.9945*10^(-9)	3.9998

结论：A矩阵维数越大，达到所要求精度需要的迭代次数越多

图1 Jacobi迭代法收敛过程

Gauss -Seidel数学原理：

由Jacobi迭代法中，每一次的迭代只用到前一次的迭代法，若每一次迭代充分利用当前最新的迭代值，即在第k+1次迭代中计算第i个分量xi(k+1)时，用最新分量x1(k+1)，x2(k+1)......xi-1(k+1)代替旧分量x1(k)，x2(k)......xi-1(k)，就得到所谓解方程组的Gauss-Seidal迭代法。

  具体做法为选取分裂矩阵A的下三角部分，即选取M=D-L,A=M-N;于是得到Gauss -Seidel迭代矩阵G=(D-L)^(-1)*U,此时Ax=b分解为(D-L)x=Ux+b再选取初始迭代向量X^(0)，开始逐次迭代

2.当n=10,20,50,100,200 时，使用Jacobi迭代求解上述线性方程组，输出Gauss -Seidel 迭代法迭代精度达到时的迭代次数及迭代矩阵的谱半径与方程组阶数n的关系。

本题利用Gauss -Seidel迭代运算结果如下表所示

n	迭代次数	误差	迭代矩阵的谱半径
10	207	4.2047*10^(-9)	3.3190
20	716	3.0290*10^(-9)	3.9777
50	3875	1.9782*10^(-9)	3.9962
100	14141	1.4070*10^(-9)	3.9990
200	51783	9.9735*10^(-9)	3.9998

结论：A矩阵维数越大，使用Gauss -Seidel方法达到所要求精度需要的迭代次数越多。但是在相同的精度要求下，Gauss -Seidel所需要的迭代次数明显更少，即使在相同迭代次数下，Gauss -Seidel迭代法计算得到的误差也要比Jacobi迭代法小很多。故Gauss -Seidel迭代法效果各方面都比Jacobi迭代法强很多

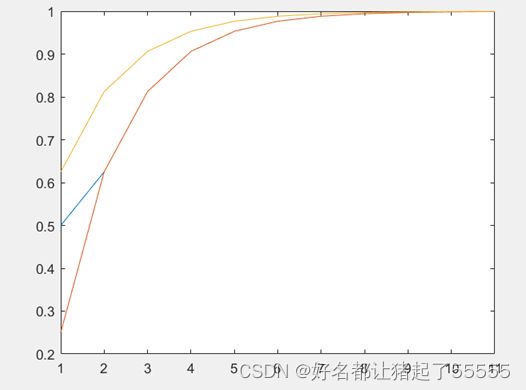
     下图为A矩阵n=3时，允许计算误差为10^(-3)时候解的收敛过程，可明显看到Gauss -Seidel迭代法解的收敛趋势更快。

图2 Gauss -Seidel迭代法收敛过程

 附录：Matlab程序迭代法求解线性方程组

% 线性方程组数值求解

产生n阶带状稀疏矩阵A，b,计算精度为accuracy

n=3;
accuracy=1e-3;
x0=zeros(1,n)';%迭代的初值为0向量
b=zeros(1,n)';
b(1)=1;
b(n)=1;
%生成所有对角元素的向量(一共有3个长度为n的对角向量，分别命名为1，2，3其中主对角线向量为diagA_2)
diagA_1=zeros(1,n)';
diagA_2=zeros(1,n)';
diagA_3=zeros(1,n)';
% 对角线-1赋值
for i=1:n-1
    diagA_1(i)=-1;
end
% 主对角线赋值
for i=1:n
    diagA_2(i)=2;
end
% 对角线+1赋值
for i=1:n-1
    diagA_3(i+1)=-1;
end
% 将5个对角向量生成一个过渡矩阵B，以及带状位置构成向量d
B=[diagA_1,diagA_2,diagA_3];
d=[-1,0,1]';
A=spdiags(B,d,n,n);
A=full(A);
% 将A分解为三个矩阵
D=diag(diag(A));%求A的对角矩阵
L=-tril(A,-1);%求A的下三角矩阵
U=-triu(A,1);%求A的上三角矩阵

Jacobi迭代法

% 将矩阵划分为x=J*x+f形式
  J=D\(L+U);%Jacobi矩阵
  f=D\b;  %f部分除以对角矩阵的逆
 
  % 进行jacobi迭代，达到所需要精度的迭代次数为k
                            x=J*x0+f;
                            k=1;
                             while norm(x-x0)>=accuracy
                                  x1(k)=x(1);
                                  x2(k)=x(2);
                                 x3(k)=x(3);
                                 x0=x;
                                 x=J*x0+f;
                                 k=k+1;
                             end
% 画图显示迭代的具体变化过程                          
  plotx=[1:k-1];
  plot(plotx,x1,plotx,x2,plotx,x3);

 Gauss-Seidel迭代法解方程

% 将矩阵分解为x=G*x0+f形式
G=(D-L)\U;% Gauss-Seidel矩阵
f=(D-L)\b;
% 进行Gauss-Seidel迭代，达到所需要精度的迭代次数为k
x=G*x0+f;
k=1;
while norm(x-x0)>=accuracy
%      x1(k)=x(1);
%     x2(k)=x(2);
%     x3(k)=x(3);
    x0=x;
    x=G*x0+f;
    k=k+1;
end
%  plotx=[1:k-1];
%  plot(plotx,x1,plotx,x2,plotx,x3);
% 计算相应的最大残差
 C=b-A*x;
 residual=norm(C,inf);
%  n阶A矩阵的谱半径
spectral_radius=max(abs(eig(A)));
% 显示最终迭代结果x，最大残差，迭代次数k和迭代矩阵谱半径
% disp(x);
disp(residual);
disp(k);
disp(spectral_radius);