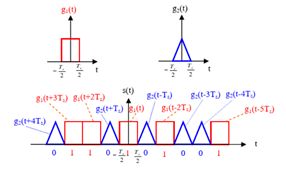
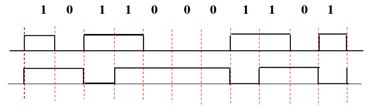
二进制基带信号的时域特性
首先我们思考什么是数字基带信号？
数字基带信号是数字信息的电波形表示。
如图的数字信号传输系统分为两个关键的部分：
- 消息与数字基带信号之间的变换；
- 数字基带信号与信道信号之间的变换。
前一个变换由发收终端设备来完成，它把无论是离散的还是连续的消息转换成数字的基带信号；而后一变换则由调制和解调器完成。
然而，在数字通信中并非所有通信系统都要经过以上两个变换过程，在某些有线信道中，特别是传输距离不太远的情况下，可以不经过调制和解调过程而让数字基带信号直接进行传输，我们称之为数字信号的基带传输，表示为下图。
基带信号即s(t)。
合理设计数字基带信号以使数字信息变换为适合于信道传输特性的频谱结构。
数字基带信号的频谱中含有丰富的低频分量乃至直流分量。
当传输距离很近时，高频分量衰减也不大。
但是数字设备之间长距离有线传输时，高频分量衰减随距离的增加而增大，同时信道中通常还存在隔直流电容或耦合变压器，因而传输频带的高频和低频部分均受限。
其次，思考什么是二进制基带信号？
数字基带信号是数字信息的电波形消息转换成数字的基带信号消息为二进制数字信号时，二进制基带信号用不同的形式（码型）表示数字信号中的 0 1
其中每个an是离散随机变量，其样本空间是{A1,A2,…,AM}
下图即一种表示二进制消息的码，1用g1，0用g2表示：
四种基本二进制基带信号波形—二进制单双极性不归零（NRZ）码
0 1 映射为幅度0、1，也可以是0映射为1，1映射为0。
不归零码可视为归零码占空比为100%的情况。
其他二进制基带信号波形
差分波形
多电平波形
二进制基带信号的频谱特性
功率谱密度：对于具有连续频谱和有限平均功率的信号或噪声，表示其频谱分量的单位带宽功率的频率函数。
频谱分析：对信号进行傅里叶变换，用该方法对振动的信号进行分解，并按频率顺序展开，使其成为频率的函数，进而在频率域中对信号进行研究和处理的一种过程。
故选择用功率谱密度来描述随机信号的频谱特性。
能量谱（分子）：原信号傅里叶变换的平方
二进制基带信号的功率谱计算方法：
1）直接根据定义计算
随机信号s(t)可写成一个确知的信号v(t)+一个均值为零的随机信号u(t)之和形式。
求v(t)的功率谱密度；
求u(t)的功率谱密度；
s(t)的功率谱密度为两者之和。
2）用自相关函数计算
求随机过程s(t)的自相关函数，
通过自相关函数与功率谱密度的傅里叶关系求得s(t)的功率谱密度。
下面对这两种方法做详细介绍：
二进制基带信号的功率谱计算方法一：定义法
稳态值v(t)：
s(t)的统计平均分量，取决于每个码元出现基波脉冲的概率加权平均，总的稳态项可写为
交变值u(t)：
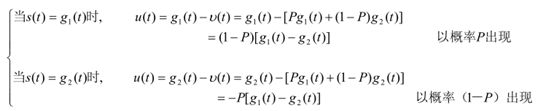
总的稳态项可写为：
1.稳态值v(t)的功率谱Pv(w)：
傅里叶级数展开
稳态值v(t)的功率谱Pv(w)
2.交变项u(t)的功率谱Pu(w)：
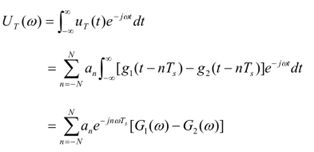
根据：
并求得：
交变项u(t)的功率谱Pu(w)（双边功率谱密度）
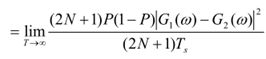
3. s(t)的功率谱
二进制基带信号的功率谱计算方法二：自相关函数法
平稳过程的自相关函数与功率谱密度是一对傅氏变换对，广义循环平稳过程也有这样的变换对关系。
对于广义循环平稳过程，平均自相关函数定义在一个周期上的平均
广义平稳随机序列：
①期望为常数
②自相关函数只与时间间隔τ有关
而这里的基带信号（随机信号）s(t)： 
① 期望与时间和周期有关（不是常数）
② 自相关函数也与周期有关
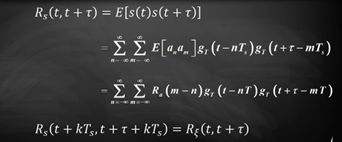
故s(t)循环平稳，
其功率谱密度就用上面提到的平均自相关函数求：
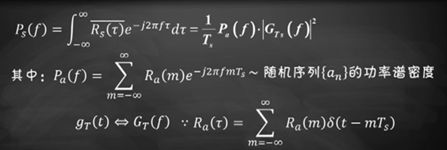
数字基带信号s(t)的功率谱密度与随机序列{an}的功率谱特性Pa(f) 以及发送滤波器的频率特性GT(f)有关。
若实随机序列{an}的各符号互不相关，功率谱密度可简化为
（3） 推导一下单极性不归零、单极性归零、双极性不归零、双极性归零四种基带信号的功率谱密度表达式，总结一下不同类型二进制基带信号功率谱密度的特点
简而言之就是代入公式！！
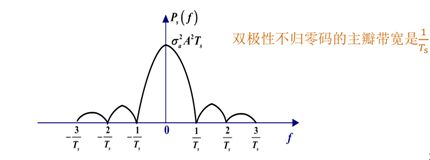
1）二进制双极性不归零（NRZ）码。
独立等概，取值±A，均值为0，方差为1
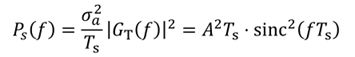
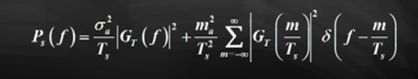
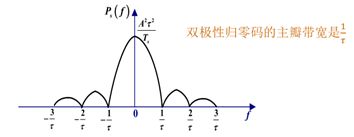
2）二进制双极性归零（RZ）码
独立等概，取值±A，均值为0，方差为1
3）二进制单极性不归零（NRZ）码
独立等概，取值0 A，可以等效为一个双极性NRZ码叠加了一个直流信号处理。
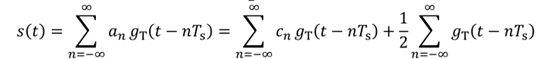
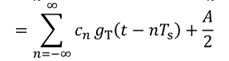
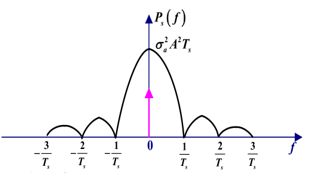
比双极性NRZ码多了个冲激信号。
4）二进制单极性归零（RZ）码
独立等概，取值0 A。
可以等效为一个双极性RZ码叠加了一个方波信号处理：
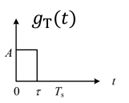
比二进制双极性归零（RZ）码多了很多个冲激信号。
三、 总结
四种二进制基带信号功率谱密度波形
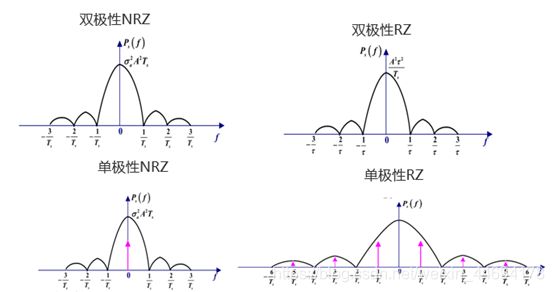
研究功率谱的意义：
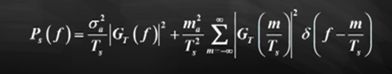
（1）根据连续谱确定序列带宽。
（2）根据离散谱是否存在明确能够从脉冲序列中直接提取定时分量，以及采用怎样的方法可以从基带脉冲序列中获得所需的离散分量。
另外，本功率谱也适用于数字调制信号。