关于ViT(Vision Transformer)的算法解读

这个我需要做一个详细的了解，因为后边的所有模型都基于此去修改。
代码出处：https://github.com/lucidrains/vit-pytorch
论文自行百度。
话不多说，先上图：

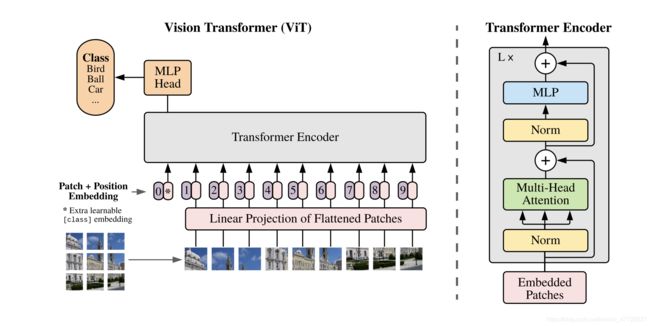
看下代码的实现：

1.参数的了解

v = ViT(
    image_size = 256,
    patch_size = 32,
    num_classes = 1000,
    dim = 1024,			# 每个向量的维度
    depth = 6,			# 就是上右图的L，就是用了几次这个Transformer Encoder
    heads = 16,			# 多头注意力机制的 多头
    mlp_dim = 2048,		# mlp的维度
    dropout = 0.1,		# 防止过拟合用的
    emb_dropout = 0.1
)

【注】关于Linear Projection of Flattened Patches

其实我刚开始一直在搜索 什么叫Linear Projection of Flattened Patches？然后都没有这个内容的讲解，其实这个东西就叫patch embeddings 大家可以看下原论文的描述，关键的我标黄了。

2.patch embeddings

就是把这个patch展平，然后压缩到dim维（对于论文中的D），我也不知道为什么要压缩到1024维，但是肯定是效果好（像传统的transformer做NLP一般用的是64维）。

        image_height, image_width = pair(image_size)		# 原图大小 比如说 256  图块大小 32
        patch_height, patch_width = pair(patch_size)		# 图块大小 

        assert image_height % patch_height == 0 and image_width % patch_width == 0, 'Image dimensions must be divisible by the patch size.'

        num_patches = (image_height // patch_height) * (image_width // patch_width) 	# (256/32)*(256/32)也就是64块
        patch_dim = channels * patch_height * patch_width		# 图块拉成 3 * 32 * 32 变成一维的长度
		
		self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1 = patch_height, p2 = patch_width),
            nn.Linear(patch_dim, dim),  # 通过线性函数 把32*32*3 -> 1024
        )

2. class(cls_token) + position embeddings

和上面代码一直，我分成了64块图片，加入位置信息，并且，多加了一个class维度，用来做分类，我的理解是，它可以整合我这64块图片的信息，最终判断这是个什么类。

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches + 1, dim))		# shape [1, 64, 1024]
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))											# shape [1, 1, 1024]
        self.dropout = nn.Dropout(emb_dropout)

3. Transformer

Transformer的一个结构 向前的过程就是实现了一个残差的过程。

class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout = 0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads = heads, dim_head = dim_head, dropout = dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout = dropout))
            ]))
    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

我们把Transformer拿出来看看，然后我后面做了注释

(transformer): Transformer(
    (layers): ModuleList(
      (0): ModuleList(
        (0): PreNorm(
          (norm): LayerNorm((1024,), eps=1e-05, elementwise_affine=True)
          (fn): Attention(				# 多头注意力Attention
            (attend): Softmax(dim=-1)
            (to_qkv): Linear(in_features=1024, out_features=3072, bias=False)		# 定义 qkv
            (to_out): Sequential(
              (0): Linear(in_features=1024, out_features=1024, bias=True)				
              (1): Dropout(p=0.1, inplace=False)
            )
          )
        )
        (1): PreNorm(			
          (norm): LayerNorm((1024,), eps=1e-05, elementwise_affine=True)
          (fn): FeedForward(			# MLP
            (net): Sequential(
              (0): Linear(in_features=1024, out_features=2048, bias=True)
              (1): GELU()
              (2): Dropout(p=0.1, inplace=False)
              (3): Linear(in_features=2048, out_features=1024, bias=True)
              (4): Dropout(p=0.1, inplace=False)
            )
          )
        )
      )

这个就是多头注意力机制 在前向传递的时候的过程。具体的函数einsum,其实就是个矩阵乘法。

	# Attention 的 forward
    def forward(self, x):
        b, n, _, h = *x.shape, self.heads
        qkv = self.to_qkv(x).chunk(3, dim = -1)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h = h), qkv)

        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale

        attn = self.attend(dots)

        out = einsum('b h i j, b h j d -> b h i d', attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

4. MLP分类

		就是一个简单MLP的简单分类了
        self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, num_classes)
        )

解读就到这里了。