TensorFlow学习记录：批量归一化（BatchNormalization）

1.批量归一化（BatchNormalization）

批量归一化是一种加快模型收敛速度的方法，并且具有一定的泛化能力。简单点说，BatchNormalization的作用就是在深层神经网络的训练过程中使得每一层神经网络的输入保持相同的分布。

因为深层神经网络在做非线性变换前的输入值Y（Y=W*x+b，Y为输入激活函数前的值，W为权重，x为输入，b为偏置），随着网络深度增加或者在训练过程中，因为输入要与权重相乘，还要经过激活函数的非线性转换，多次进行上述过程（前向传播）后，其分布逐渐发生偏移，之所以训练收敛慢，是因为Y逐渐朝非线性函数（激活函数）的取值区间的上下两个极端移动（对于Sigmoid来说，Y的取值），所以在反向传播的时候靠近输入端的神经网络的权重的梯度可能会消失（梯度消失）。为了避免由这种情况造成的梯度消失，Y在进入非线性函数前，使用BatchNormalization的方法，将Y的分布拉回到均差为0标准差为1的标准正态分布，其实就是把越来越偏的分布拉回到标准正态分布，这样使得Y落在非线性函数对输入比较敏感的分布上，在反向传播时梯度不容易消失。

其实一句话就是：对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。因为梯度一直都能保持比较大的状态，所以很明显对神经网络的参数调整效率比较高，就是变动大，就是说向损失函数最优值迈动的步子大，也就是说收敛地快。（原话引自这里）

下图为均值为0方差为1的标准正态分布图

下图为sigmoid函数的图像,$sigmoid(x)=\frac{1}{1+e^{-x}}$，这里sigmoid(x)中的x等于上面的Y

下图为sigmoid的导数图像,$sigmoid‘(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=sigmoid(x)\ast (1-sigmoid(x))$
横坐标为sigmoid(x)，纵坐标为sigmoid’(x)

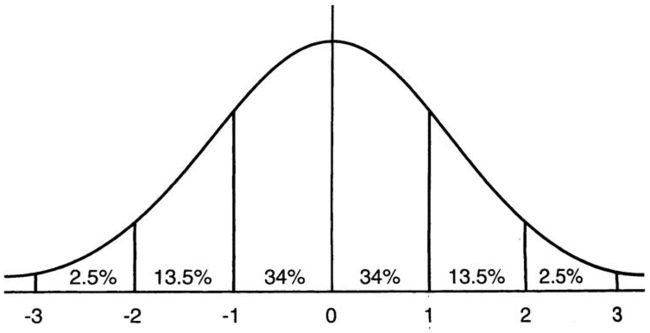
可以看到，第二张图中非线性函数sigmoid(x)在x$ϵ$[-2,2]时的图像是比较陡峭的，超过区间[-2,2]后的图像趋于平稳，结合第三张图可知道，即在x$ϵ$[-2,2]时sigmoid‘(x)比较大一点，超过区间[-2,2]后sigmoid’(x)比较小一点。由第一张图可以得知在标准正态分布中[-2,2]之间的数据占了总数据的95%，BatchNormalization的目的就是把Y在输入激活函数前拉回到均值为0方差为1的标准正态分布上，使Y值尽量分布在[-2,2]上，sigmoid(x)在x$ϵ$[-2,2]时梯度比较大，相关参数才会很明显地得到更新学习。

2.TensorFlow中BatchNormalization的正确使用

TensorFlow中实现BatchNormalization的函数主要有下面4个：

（1）slim.batch_norm()
（2）tf.nn.batch_normalization()
（3）tf.layers_batch_normalization()
（4）tf.contrib.layers.batch_norm()

（1）slim.batch_norm()

slim.batch_norm()的参数的含义如下:（转自这里）

slim.batch_norm('is_training': is_training,
        # 是否是在训练模式，如果是在训练阶段，将会使用指数衰减函数（衰减系数为指定的decay），
        # 对moving_mean和moving_variance进行统计特性的动量更新，也就是进行使用指数衰减函数对均值和方
        # 差进行更新,而如果是在测试阶段，均值和方差就是固定不变的，是在训练阶段就求好的，在训练阶段，
        # 每个批的均值和方差的更新是加上了一个指数衰减函数，而最后求得的整个训练样本的均值和方差就是所
        # 有批的均值的均值，和所有批的方差的无偏估计
 
        'zero_debias_moving_mean': True,
        # 如果为True，将会创建一个新的变量对 'moving_mean/biased' and 'moving_mean/local_step'，
        # 默认设置为False，将其设为True可以增加稳定性
 
        'decay': batch_norm_decay,             # Decay for the moving averages.
        # 该参数能够衡量使用指数衰减函数更新均值方差时，更新的速度，取值通常在0.999-0.99-0.9之间，值
        # 越小，代表更新速度越快，而值太大的话，有可能会导致均值方差更新太慢，而最后变成一个常量1，而
        # 这个值会导致模型性能较低很多.另外，如果出现过拟合时，也可以考虑增加均值和方差的更新速度，也
        # 就是减小decay
 
        'epsilon': batch_norm_epsilon,         # 就是在归一化时，除以方差时，防止方差为0而加上的一个数
        'scale': batch_norm_scale,
        'updates_collections': tf.GraphKeys.UPDATE_OPS,    
        # force in-place updates of mean and variance estimates
        # 该参数有一个默认值，ops.GraphKeys.UPDATE_OPS，当取默认值时，slim会在当前批训练完成后再更新均
        # 值和方差，这样会存在一个问题，就是当前批数据使用的均值和方差总是慢一拍，最后导致训练出来的模
        # 型性能较差。所以，一般需要将该值设为None，这样slim进行批处理时，会对均值和方差进行即时更新，
        # 批处理使用的就是最新的均值和方差。
        #
        # 另外，不论是即时更新还是一步训练后再对所有均值方差一起更新，对测试数据是没有影响的，即测试数
        # 据使用的都是保存的模型中的均值方差数据，但是如果你在训练中需要测试，而忘了将is_training这个值
        # 改成false，那么这批测试数据将会综合当前批数据的均值方差和训练数据的均值方差。而这样做应该是不
        # 正确的。
      )

（2）tf.nn.batch_normalization()

这个函数的使用过程要分为两步使用，即首先要计算当前batch的均值mean和方差variance，封装程度不高，不推荐使用。
首先计算当前batch的均值mean和方差variance：

a_mean,a_var = tf.nn.moments(x,axes,name=None,keep_deims=False)
# 其中x为输入的数据，axes为要计算x哪个维度上的均值mean和方差variance
# 该函数计算返回x的均值mean和方差variance

然后再使用tf.nn.batch_normalization()实现BatchNormalization

net = tf.nn.batch_normalization(x,
mean = a_mean,  # 使用上面计算出来的均值a_mean
variance = a_var,  # 使用上面计算出来的方差a_var
offset,   # 同上
scale,    # 同上 
variance_epsilon,   #同上
name = None)

（3）tf.layers_batch_normalization()

TensorFlow官网中的说明

tf.layers.batch_normalization(
    inputs,
    axis=-1,
    momentum=0.99,   #滑动平均的动量，用于在训练期间每个batch都计算滑动平均维护当前batch下的均值mean和方差variance，然后保存起来，在测试的时候就直接使用保存起来的均值mean和方差variance
    epsilon=0.001,
    center=True,
    scale=True,
    beta_initializer=tf.zeros_initializer(),
    gamma_initializer=tf.ones_initializer(),
    moving_mean_initializer=tf.zeros_initializer(),
    moving_variance_initializer=tf.ones_initializer(),
    beta_regularizer=None,
    gamma_regularizer=None,
    beta_constraint=None,
    gamma_constraint=None,
    training=False,
    trainable=True,
    name=None,
    reuse=None,
    renorm=False,
    renorm_clipping=None,
    renorm_momentum=0.99,
    fused=None,
    virtual_batch_size=None,
    adjustment=None
)

在训练时均值mean和方差variance的计算公式如下(类似于神经网络中权重滑动平均值的计算)：

training_mean = momentum * (上一个batch的training_mean) + (1-momentum) * (当前batch的mean)
traingint_var = momentum * (上一个batch的trainging_var) + (1-momentum)*(当前batch的variance)

一般使用的时候可以直接这样写，其它参数可以忽略

# 训练时
output = tf.layers.batch_normalization(x,trainging=True)

# 测试时
output = tf.layers.batch_normalization(x,trainging=False)

另外，最重要的是，当要使用tf.layers_batch_normalization()时，在启动会话Session前要记得加入以下代码tf.layers_batch_normalization()才能起作用

update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops): #要先执行完update_ops操作后才能开始学习
	train_op = optimizer.minimize(loss)

（4）tf.contrib.layers.batch_norm()

tf.contrib.layers.batch_norm()的用法和tf.nn.batch_normalization()差不多。以下是TensorFlow官网关于tf.contrib.layers.batch_norm()的餐数的说明：

tf.contrib.layers.batch_norm(
    inputs,
    decay=0.999,#衰减系数。合适的衰减系数值接近1.0,特别是含多个9的值：0.999,0.99,0.9。如果训练集表现很好而验证/测试集表现得不好，选择小的系数（推荐使用0.9）。
    center=True,
    scale=False,#如果为True，则乘以gamma。如果为False，gamma则不使用。当下一层是线性的时（例如nn.relu），由于缩放可以由下一层完成，所以可以禁用该层。
    epsilon=0.001,
    activation_fn=None,
    param_initializers=None,# beta, gamma, moving mean 和 moving variance的优化初始化
    param_regularizers=None,# beta and gamma正则化优化，只有在is_training=True才起效
    updates_collections=tf.GraphKeys.UPDATE_OPS,
    is_training=True,
    reuse=None,
    variables_collections=None,
    outputs_collections=None,
    trainable=True,
    batch_weights=None,
    fused=None,
    data_format=DATA_FORMAT_NHWC,
    zero_debias_moving_mean=False,#如果想要提高稳定性，zero_debias_moving_mean设为True
    scope=None,
    renorm=False,
    renorm_clipping=None,
    renorm_decay=0.99,
    adjustment=None
)

使用时同样也要加入下面的代码

update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops): #要先执行完update_ops操作后才能开始学习
	train_op = optimizer.minimize(loss)