智能算法之模拟退火算法

1.起源

模拟退火算法来源于热力学中固体物质的退火冷却过程 (退火是一种金属热处理工艺，指的是将金属缓慢加热到一定温度，保持足够时间，然后以适宜速度冷却)。

2.物理退火流程

模拟退火的算法思想是参考物理退火的过程而来，物理退火的过程为：加温过程 -> 等温过程 -> 冷却过程。

2.1 加温过程

通过加温，增强粒子的热运动，让各部分变得均匀。当温度足够高时，固体将熔解为液体，从而消除原先系统中可能存在的非均匀状态，保证后续进行的过程是从平衡态开始，由于是加温过程温度上升，所以该过程系统能量增加。

2.2 等温过程

对于与周围环境交换热量而温度保持不变的封闭系统，系统状态的自发变化总是朝着自由能减少的方向进行，当自由能达到最小时，系统达到平衡态。

2.3 冷却过程

通过一定速率对液体进行冷却，减弱粒子的热运动并趋于有序，在每个温度都达到平衡态，最后在常温时达到基态，能量减为最小，从而得到低能态的晶体结构。

2.4 组合优化与物理退化

组合优化	物理退火
解	粒子状态
最优解	能量最低态
设定初温	熔解过程
$Metropolis$ 抽样过程	等温过程
控制参数下降	冷却过程
目标函数	能量

3.原理

模拟退火算法的基本原理：对于目标函数 $f(X)$、自变量为 $X$ 的 $n$ 维极小化问题（极大化问题乘以$-1$转化为极小化问题），初值 $X_0$ 可以随机化或者自己设置。

3.1 算法核心迭代

设 $f_k,f_{k+1}$ 分别为目标函数在第 $k$ 次和第 $k+1$ 次迭代值，即 $f_k=f(X_k),f_{k+1}=f(X_{k+1})$。
若 $f_k>f_{k+1}$，则接受 $X_{k+1}$ 作为下一次迭代的初值继续进行运算，直至满足终止条件（收敛或者迭代次数耗尽）；
若 $f_k<f_{k+1}$，则接受 $X_{k+1}$ 的概率为 $p$，拒绝的概率为 $1-p$，其中接受概率公式如下：$$p=exp(-\frac{f_{k+1}-f_k}{T})$$ 其中 $T$ 为控制参数，在模拟退火算法中，$T$ 必须缓慢减少，避免变化过快，导致优化陷入极值点。

3.2 具体流程

以求解极小值问题为例：
$（1）$设定初始温度 $T$，迭代次数 $L$，误差 $ϵ$，初始解 $X_0$，得到目标函数$f(X_0)$；
$（2）$循环进行迭代，$k=1,\cdots ,L$；
$（3）$根据当前温度得到新解 $X^{\prime }$(第一个可以随机生成)， 代入 $f(X)$ 得到 $f(X^{\prime })$；
$（4）$若 $f(X)>f(X^{\prime })$，则接受 $X^{\prime }$ 作为下一次迭代的初值，若 $f(X)<f(X^{\prime })$，则以概率 $exp(-\frac{f(X^{\prime })-f(X)}{T})$ 接受 $X^{\prime }$ 作为下一次迭代的初值；
$（5）$若满足终止条件，则输出当前最优解 $X^{\prime }$，终止条件；
$（6）$$T$ 减小，然后回到流程$（2）$，在当前温度下继续循环迭代，执行步骤$（3，4，5）$；
$（7）$注意，这里的终止条件可以有多个，比如：迭代次数耗尽、满足最优解、温度降低到一定值、新目标函数与原先目标函数的误差小于 $ϵ$。

4.案例

4.1 求解n元函数的极小值

例1：求解函数 $f(X)=X^2$ 的最小值，其中 $X^2={\sum }_{i=1}^{10}{x}^2$，$-10\le x\le 10$。
下面通过matlab进行求解：
目标函数：

%--------目标函数f(x)---------
function result = func1(x)
    result = sum(x.^2);
end

模拟退火算法：

clear; clc;

%---------------------模拟退火核心-------------------------------
L = 200;                           % 每个温度的迭代次数
epsilon = 1e-10;                   % 新目标函数与原先目标函数的误差
T0 = 200;                          % 初始温度
T1 = 0.00001;                      % 终止温度
s = 0.01;                          % 自变量更新的步长，相当于学习率
K = 0.998;                         % 温度衰减参数
P = 0;                             % Metropolis 过程中总接受点

%---------------------根据题目所写--------------------------------
opt_minmax = 1;                    % 求解极小值问题为1，极大值问题为-1
n = 10;                            % 自变量维度
up = 10;                           % 自变量上限
sup = -10;                         % 自变量下限
x0 = rand(n, 1)*(up-sup)-up;       % 随机生成在范围内的初始自变量
x1 = rand(n, 1)*(up-sup)-up;       % 随机生成在范围内的 x1 自变量进行第一步
PreBest = x0;
NowBest = x1; 

%---------------------进行迭代----------------------------------
delta = abs(func1(NowBest) - func1(PreBest));
while (delta > epsilon) && (T0 > T1)
    T0 = K*T0;
    for i = 1:L
        x2 = x1 + s*(rand(n, 1)*(up-sup)-up);
        %-----下面这个循环是写题目的条件的，这里没啥好些，就重复了边界条件
        for j = 1:n
            while (x2(j) > up) || (x2(j) < sup)
                x2(j) = x1(j) + s*(rand*(up-sup)-up);
            end
        end
        %--------------查看解是否是全局最优解----------------
        if opt_minmax*func1(NowBest) > opt_minmax*func1(x2)
            PreBest = NowBest;             % 保留上一个最优解
            NowBest = x2;                  % 保留新的最优解
        end
        %---------------- Metropolis过程--------------------
        if opt_minmax*func1(x1) > opt_minmax*func1(x2)
            x1 = x2;
            P = P + 1;
        else
            p = exp(-(func1(x2)-func1(x1))/T0);
            if p > rand(1)
                x1 = x2;
                P = P + 1;
            end
        end
        Y(P) = func1(NowBest);
    end
    delta = abs(func1(NowBest) - func1(PreBest));
end

得到结果为：
$X=[-0.0114,-0.0002,0.0020,0.0101,0.0074,-0.0003,-0.0084,0.0112,-0.0252,0.0052]$

$f(X)=0.0011$
绘制适应度进化曲线：

%----------------------------画图--------------------------------
plot(Y, 'r');
hold on
scatter(length(Y), Y(end), 'bo', 'MarkerFaceColor', 'b')
text(length(Y), Y(end), ' 最优点')
xlabel('迭代次数'); ylabel('目标函数值'); title('适应度进化曲线');

4.2 求解二元函数的极小值

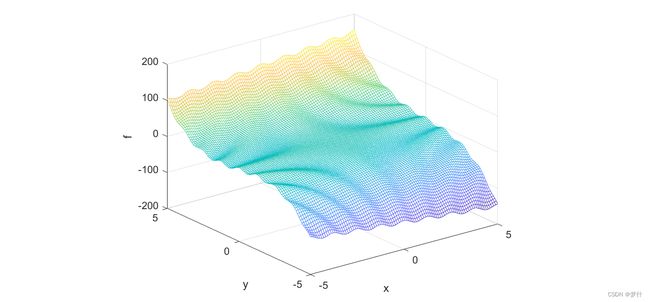
例2：求解函数 $f(x,y)=5cos(xy)+xy+y^3$ 的最小值，其中 $-5\le x\le 5,-5\le y\le 5$。
下面通过matlab进行求解：
目标函数：

%--------目标函数f(x)---------------
function result = func1(x)
    result = 5*cos(x(1).*x(2))+x(1).*x(2)+x(2).^3;
end

可以看看 $f(x,y)$ 的图像：

clear;clc;
x = linspace(-5, 5);
y = linspace(-5, 5);
[x, y] = meshgrid(x, y);
f = 5*cos(x.*y)+x.*y+y.^3;
mesh(x, y, f);
xlabel('x'); ylabel('y'); zlabel('f');

第二种方法适合小白，不过和meshgrid画出来的图相比较发现是翻转过的，所以可以自行选择。

x1 = linspace(-5, 5);
y1 = linspace(-5, 5);
N = size(x1, 2);
for i = 1:N
    for j = 1:N
        z(i, j)=5*cos(x1(i)*y1(j))+x1(i)*y1(j)+y1(j)^3;
    end
end
mesh(x1, y1, z);
xlabel('x1'); ylabel('y1'); zlabel('z');

模拟退火算法：

clear; clc;

%---------------------模拟退火核心------------------------------------------
L = 200;                             % 每个温度的迭代次数
epsilon = 1e-8;                      % 新目标函数与原先目标函数的误差
T0 = 200;                            % 初始温度
T1 = 0.00001;                        % 终止温度
s = 0.01;                            % 自变量更新的步长，相当于学习率
K = 0.998;                           % 温度衰减参数
P = 0;                               % Metropolis 过程中总接受点

%---------------------根据题目所写------------------------------------------
opt_minmax = 1;                      % 求解极小值问题为1，极大值问题为-1
n = 2;                               % 自变量维度
up = [5; 5];                         % 自变量x,y上限
sup = [-5; -5];                      % 自变量x,y下限
x0 = rand(2, 1).*(up-sup)-up;        % 随机生成在范围内的初始自变量x0,y0
x1 = rand(2, 1).*(up-sup)-up;        % 随机生成在范围内的 x1, y1 自变量进行第一步
PreBest = x0;
NowBest = x1; 

%---------------------进行迭代----------------------------------------------
delta = abs(func1(NowBest) - func1(PreBest));
while (delta > epsilon) && (T0 > T1)
    T0 = K*T0;
    for i = 1:L
        x2 = x1 + s*(rand(n, 1).*(up-sup)-up);
        %-----下面这个循环是写题目的条件的，这里没啥好些，就重复了边界条件
        for j = 1:n
            while (x2(j) > up(j)) || (x2(j) < sup(j))
                x2(j) = x1(j) + s*(rand*(up(j)-sup(j))-up(j));
            end
        end
        %--------------查看解是否是全局最优解----------------
        if opt_minmax*func1(NowBest) > opt_minmax*func1(x2)
            PreBest = NowBest;             % 保留上一个最优解
            NowBest = x2;                  % 保留新的最优解
        end
        %---------------- Metropolis过程--------------------
        if opt_minmax*func1(x1) > opt_minmax*func1(x2)
            x1 = x2;
            P = P + 1;
        else
            p = exp(-(func1(x2)-func1(x1))/T0);
            if p > rand(1)
                x1 = x2;
                P = P + 1;
            end
        end
        Y(P) = func1(NowBest);
    end
    delta = abs(func1(NowBest) - func1(PreBest));
end

得到结果为：
$f(x,y)=f(4.4394,-5.0000)=-152.0912$
绘制适应度进化曲线：

%----------------------------画图--------------------------------
plot(Y, 'r');
hold on
scatter(length(Y), Y(end), 'bo', 'MarkerFaceColor', 'b')
text(length(Y), Y(end), ' 最优点')
xlabel('迭代次数'); ylabel('目标函数值'); title('适应度进化曲线');

4.3 共享单车配送规划

若某地共享单车存放点有 $n$ 个，每个存放点需求量为 $q_i(i=1,2,\cdots ,n)$，有 $m$ 辆配送车进行配送，每辆车都型号都一致，最大装载量为 $Q$，存放点 $i$ 到存放点 $j$ 的距离为 $d_{ij}$，记配送中心为 $o$，则配送中心到存放点的距离为 $d_{oi}(i=1,2,\cdots ,n)$，每条路线的共享单车需求量之和不超过配送车最大装载量 $Q$；每次配送都会产生费用和损耗：费用有固定成本 $c_0$ 和行驶费用 $c_1$，损耗有运输损耗比例 ${\beta }_1$ 和装卸损耗 ${\beta }_2$，注意：这里假设单位时间的损耗为 $0$，也就是时间对共享单车质量的影响微乎其微。给此地的共享单车配送路线进行规划，让资源达到最大的利用。

5.优缺点及可改进方向