PF-Net: Point Fractal Network for 3D Point Cloud Completion

PF-Net:用于三维点云补全的点分形网络

Abstract

  在本文中，我们提出了一种点分形网络（PF-Net），一种新的基于学习的精确高保真点云补全方法。与现有点云补全网络不同，现有点云补全网络从不完整的点云生成点云的整体形状，并且总是改变现有点，并遇到噪声和几何损失，PF-Net保留了不完全点云的空间排列，并能计算出预测中缺失区域的详细几何结构。为了完成这项任务，PF-Net利用基于特征点的多尺度生成网络分层估计缺失的点云。此外，我们将多阶段完成损失和对抗损失相加，以生成更真实的缺失区域。对抗性损失可以更好地处理预测中的多种模式。我们的实验证明了我们的方法对于几个具有挑战性的点云完成任务的有效性。

1.Introduce

  三维视觉是当前研究的热点之一。在各种类型的三维数据描述中，点云由于其较小的数据量但更精细的表示能力而被广泛应用于三维数据处理[1–3]。现实世界中的点云数据通常使用激光扫描仪、立体相机或低成本RGB-D扫描仪捕获。但是，由于遮挡、光反射、表面材质的透明度以及传感器分辨率和视角的限制，会导致几何和语义信息的丢失，从而导致不完整的点云。因此，修复不完整的点云是进一步应用的一项重要任务。由于三维点云是非结构化和无序的，大多数基于深度学习的三维数据处理方法将点云转换为图像集合（如视图）或基于体素的三维数据表示形式。然而，多视图和基于体素的表示[4–9]会导致不必要的体积，并限制体素的输出分辨率[10,11]。

图1。我们的PF-Net以不完整的点云为输入，直接预测缺失的点云。多尺度预测的显示（用蓝色、红色和黄色表示）由不同深度的点金字塔解码器（PPD）分层显示。低分辨率预测作为生成高分辨率预测的中心点，导致从粗到精的预测。

  由于PointNet[10]的出现，基于学习的体系结构能够直接对点云数据进行操作。L-GAN[12]介绍了第一个基于深度学习的网络，该网络利用编码器-解码器框架完成点云计算。PCN[11]结合了L-GAN[12]和FoldingNet[13]的优点，后者专门用于修复不完整的点云。最近，RL-GANNet[14]提出了一种强化学习代理控制的GAN，用于缩短点云补全的预测时间。
  以前的完成工作以不完整的点云为输入，目标是输出整体完整的模型。他们更注重学习类/种类的一般特征，而不是特定对象的局部细节。因此，它们可能会改变已知点的位置，并遇到类别扭曲[13]，从而导致噪声和详细的几何损失。例如，在图6（3）中，先前作品中椅子的重建遗漏了现有的横杆（椅子下方），并且无法生成空心靠背。原因可能是自动编码器倾向于平均预测中的多个“椅子”。注意到训练集中的大多数椅子都是完全填充靠背而没有横杆的，如图1所示，因此先前的网络更可能生成具有完全填充靠背的正常椅子，而不是图6（3）中带有空心靠背和横杆的“特殊”椅子。在这项工作中，我们提出了点分形网络（PF-Net）修复不完整的点云。与现有的自动编码器体系结构不同，PF-Net的主要特点可概括如下：
  （1） 为了保持原始部分的空间排列，我们将部分点云作为输入，只输出点云的缺失部分，而不是整个对象。该体系结构有两个优点：首先，修复后保留了原始点云的几何特征。其次，它有助于网络专注于感知缺失部分的位置和结构。这种预测的主要困难在于，部分已知点和待推断点仅在语义层面上相关，在空间排列上完全不同。
  （2） 为了更好地提取特定部分点云的特征，我们首先提出了一种新的多分辨率编码器（MRE），利用一种新的特征提取器结合多层感知机（CMLP）从部分点云及其低分辨率特征点提取多层特征。这些多尺度特征既包含局部特征又包含全局特征，还包含低层特征和高层特征，增强了网络提取语义和几何信息的能力。
  （3） 为了解决亏格扭曲问题[13]并生成细粒度缺失区域，我们设计了一个点金字塔解码器（PPD）来分层生成缺失点云。PPD是一种基于特征点的多尺度生成网络。PPD将从不同深度的地层中预测主要、次要和详细点。主点和次点将尝试匹配其相应的特征点，并用作骨架中心点，以将总体几何体信息传播到最终细节点。图1显示了该分层预测的过程，其显示了在生成高质量缺失区域点云和恢复原始详细形状方面的优异性能。
此外，我们还提出了一种多阶段补全损失预测方法，以指导该方法的预测。多阶段完成损失有助于网络更加关注特征点。为了进一步缓解由自动编码器框架引起的失真问题，受著名2D上下文编码器[15]的启发，我们通过联合训练PF网络，将多阶段补全损失和对抗损失降至最低，从而减少损失函数中的负担。对抗性损失优化了我们的网络，使其能够从多种模式中选择特定的点云。

2.Related Work

2.1.形状补全和深度学习

  目前，三维形状补全方法主要基于三维体素网格和点云。对于基于体素网格的算法，已经开发了3D RecGAN[16]、3D-Encoder-Predictor Networks（3D-EPN）[17]以及3D-ED-GAN和LRCN[18]的混合框架等体系结构，以实现修复不完整输入数据的目标。然而，基于体素的方法受到分辨率的限制，因为计算成本随着分辨率的增加而急剧增加。
  PointNet[10]解决了处理无序点集的问题。因此，可以在无序点上直接执行形状补全任务的算法得到了极大的发展[19–23]。L-GAN[12]为点云引入了第一个深度生成模型。虽然L-GAN[12]在某种程度上能够执行形状补全任务，但其架构主要不是为了完成形状补全任务而构建的，因此性能并不理想。FoldingNet[13]引入了一种名为Folding的新的解码操作名为折叠，用作2D到3D映射。后来，点云补全网络（PCN）[11]提出了第一个基于学习的体系结构，重点关注形状补全任务。PCN[11]应用折叠操作[13]来近似相对光滑的表面并进行形状完成。最近，发明了一种强化学习代理控制的基于GAN的网络（RL-GAN-Net）[14]，用于实时点云补全。文献[14]中使用了RL代理，以避免复杂的优化并加快预测过程，但它并不注重提高点的预测精度。3D点胶囊网络[24,25]超越了其他方法的性能，成为处理点云的最先进的自动编码器，特别是在点云重建领域。

2.2.上下文编码和特征金字塔网络

  上下文编码器[15]处理缺失区域的图像，并训练卷积神经网络来回归缺失的像素值。该架构由捕获图像未损坏内容的编码器和预测丢失图像内容的解码器组成。此外，它还联合训练语义修复的重建和对抗性损失。
  特征金字塔网络（FPN）[26]是解决多尺度特征提取问题的有效方法。多亏了FPN的体系结构[26]，最终的特征图融合了语义丰富和局部丰富的特征[27–31]。它增强了最终特征图中包含的几何和语义信息。FPN[26]部分启发了我们网络中的解码器。

图2.PF-Net的体系结构。PF-Net的输入是不完整的点云，它利用多尺度生成网络PPD预测缺失的点云。IFPS（第3.1节）将输入（用黄色表示）采样到不同的尺度（用红色和蓝色表示）。图中的蓝色、红色和黄色（最终预测）表示三个预测尺度。CMLP（第3.2节）是我们的特征提取器。CD（第3.4节中的倒角距离）用于评估预测值与地面真实值之间的差异。

3.Method

  在本节中，我们将介绍我们的PF网络，它根据不完整的已知配置预测点云的缺失区域。图2显示了我们PF网络的完整架构。我们的PF网络的总体架构由三个基本构建块组成，即多分辨率编码器（MRE）、点金字塔解码器（PPD）和鉴别器网络。

3.1.特征点采样

  在点云中，我们只能取少量的点来描述形状，这些点被定义为特征点。换句话说，特征点映射点云的骨架[32]。为了从点云中提取特征点，我们使用迭代最远点采样（IFPS），这是Pointnet++[33]中应用的一种采样策略，用于获取一组骨架点。与随机抽样相比，IFP可以更好地表示整个点集的分布，并且比CNN更有效[33]。在图3中，我们可视化了IFP的效果。即使我们只提取了6.25%的点，这些点仍然可以描述灯的配置，并且灯的主要几何结构没有被破坏。

3.2.多分辨率编码器

  CMLP我们首先介绍了MRE的特征提取器，称为组合多层感知（CMLP）。在以前的大多数工作中，编码器的特征提取是多层感知（MLP）。我们将其称为PointNet MLP，如图4（a）所示。该方法将每个点映射到不同的维度，并从最终维度中提取最大值以形成全局潜在向量。但是，它没有充分利用包含丰富本地信息的低级和中级功能。此外，L-GAN[12]和PointNet[10]表明，此功能提取器的性能受到Maxpooling层维度的强烈影响，即，在CMLP中，我们还使用MLP将每个点编码为多个维度[64]−128−256−512−1024]. 与MLP不同，我们将MLP最后四层的输出最大化，以获得多维特征向量fi，其中大小fi:=1282565121024，对于i=1，…，4。然后将所有fi连接起来，形成组合的潜在矢量F。SizeF:=1920，它同时包含低级和高级特征信息。

图3.不同分辨率的IFPS结果。蓝色灯有2048个点。从蓝色灯中分别采样512、256和128个点的三个紫色灯。

  我们的多分辨率编码器的输入是一个N×3无序点云。我们使用IFPS对输入点云进行下采样，以获得两个不同分辨率的尺度（大小：nk×3和nk2×3）。我们使用这种依赖于数据的方式来获取输入点集的特征点，帮助编码器关注那些更具代表性的点。对于i=1,2,3，将使用三个独立的CMLP将这三个尺度映射为三个单独的组合潜在向量Fi。每个向量表示从点云的特定分辨率中提取的特征。然后，所有这些图形连接起来，形成一个最小为1920×3的潜在特征图（即，三个矢量的大小各为1920）。然后，我们使用MLP[3-1]将潜在特征映射集成到最终的特征向量中。v的大小=1920。

3.3.点金字塔解码器

  解码器接收最终的特征向量输入并输出m×3点云，该点云表示缺失区域的形状。我们的PPD的基线是完全连接的解码器[12]。完全连接的解码器擅长预测点云的全局几何结构。然而，由于它仅使用最后一层来预测形状，因此总是会导致局部几何信息的丢失。以前的工作将完全连接的解码器与基于折叠的解码器相结合，以增强预测形状的局部几何结构。然而，如[13]所示，如果原始曲面相对复杂，基于折叠的解码器不善于处理亏格失真和保留原始详细几何体。为了克服这一局限性，我们将PPD设计为基于特征点的层次结构，其灵感来自FPN[26]。PPD的细节如图5所示。我们首先通过将V穿过完全连接的层来获得三个特征层FCi（大小FCi:=1024、512、256个神经元，对于i=1、2、3）。每个要素层负责以不同的分辨率预测点云。一次中心点Yprimary将从最深的FC3开始预测，其大小为M1×3。然后，FC2将用于预测次级中心点的相对坐标。Yprimary中的每个点都将用作生成Yprimary的M2M1点的中心点。我们使用“扩展”和“添加”操作来实现这个过程。因此，Ysecondary的尺寸为M2×3。细节点Ydetail是PPD的最终预测。Ydetail的生成类似于图5所示的Y二次生成。尺寸：M×3。同时，Ydetail将尝试匹配从G.T.采样的特征点。由于这种多尺度生成架构，高层次特征将影响低层次特征的表达，低分辨率特征点可以将局部几何信息传播到高分辨率预测。我们的实验表明，PPD预测具有较少的失真，并且能够保留原始缺失点云的详细几何结构。

图4.3D点编码器的两个不同特征提取器的比较。PointNet-MLP仅使用最后一个单层来提取潜在向量。我们的CMLP通过连接来自最后四层的多维潜在向量来映射组合的潜在向量。它可以更好地利用高级和低级功能。

3.4.损失函数

  我们的PF-Net的损失函数由两部分组成：多阶段补全损失和对抗损失。补全损失测量缺失点云的地面真实值与预测点云之间的差异。对抗性损失试图通过优化MRE和PPD使预测看起来更真实。Ygt的尺寸为M×3，与Ddetail相同。

图5.点金字塔解码器的详细信息。PPD在升序尺度上给出了三个连接层的输出，在语义和几何层面上都是相似的。直观地说，PPD的架构反映了数学中的“分形几何”概念。

  多阶段补全损失Fan等人的研究。[34]提出了两种比较无序点云的排列不变度量：倒角距离(CD)和土方距离(EMD)。在这项工作中，我们选择倒角距离作为完全性损失，因为与EMD相比，倒角距离具有可微性和更高的计算效率。

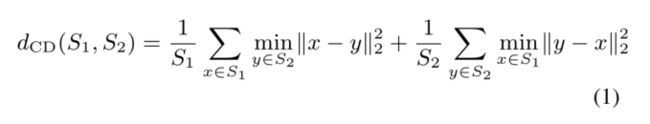
  Cd in(1)测量预测点云S1和地面真值点云S2之间的平均最近平方距离。由于点金字塔解码器将预测三个不同分辨率的点云，我们的多级完成损失由(2)中的dCD1、dCD2和dCD3三项组成，由超参数α加权。第一项计算细节点Ydetail和缺失区域Ygt的地面真相之间的平方距离。第二项和第三项分别计算一次中心点Yprimary一次、次要中心点Ysecondary次要与二次采样地面实值Y‘gt、Y’’gt之间的平方距离。下采样的地面真值Y‘gt和Y’’gt分别与Yprimary(M1×3)和Ysecondary(M2×3)大小相同。我们通过应用IFPS从YGT得到Y‘gT和Y’’gT。它们是缺失区域的特征点。多级完井损失的设计提高了特征点的比例，使其更好地聚焦于特征点。

  对抗性损失本工作中的对抗性损失的灵感来自生成性对抗性网络(GAN)[35]。我们首先定义了F()：=PPD(MRE())，其中MRE是多分辨率编码器，PPD是点金字塔解码器。F：X→Y‘会将部分输入X映射到预测的缺失区域Y’。然后，鉴别器(D())尝试区分预测缺失区域Y‘和实际缺失区域Y。该鉴别器是一个与CMLP结构相似的分类网络。具体的结构有连续的MLP层[64−64−128−256]，我们最大限度地池化最后三层的响应，得到特征向量fi，其中fi的大小为：=64,128,256，对于i=1，2，3，将它们连接成一个潜在向量F。F的大小为448，F将通过全连通层[256,128，16，1]，然后用Sigmoid分类器得到预测值。我们现在定义对抗性损失：

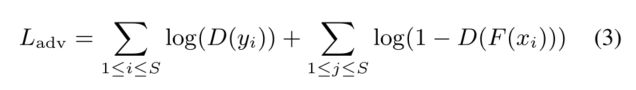
  式中Xi∈X，yi∈Y，i=1，.。。。，S.S是X，Y的数据集大小，F和D在训练时使用交替的Adam进行联合优化。
  λcom和λadv是补全损失和对抗性损失的权重，满足以下条件：λcom+λadv=1。

4.Experiments

4.1.数据生成和实现细节

  为了训练我们的模型，我们使用基准数据集Shapenet-Part[36]中的13个不同对象类别。形状总数为14473个(11705个用于培训，2,768个用于测试)。所有输入点云数据都以原点为中心，其坐标被规格化为[-1，1]。地面真实点云数据是通过在每个形状上均匀采样2048个点来创建的。不完整的点云数据是通过在多个视点中随机选择一个视点作为中心，并从完整数据中删除一定半径内的点来生成的。我们控制半径以获得不同数量的缺失点。在与其他方法进行比较时，我们将缺失25%的原始数据的不完整点云设置为训练和测试。
  我们在PyTorch上实现我们的网络。所有三个构建块都是通过交替使用ADAM优化器进行训练的，初始学习率为0.0001，批大小为36。我们在MRE和鉴别器中使用批归一化(BN)和REU激活单元，但在PPD中只使用REU激活单元(最后一层除外)。在MRE中，我们设置k=2。在PPD中，我们根据每个形状的点数设置M1=64，M2=128。我们只改变M来控制最终预测的大小。

4.2.点云补全结果

  在这一小节中，我们将把我们的方法与几种直接在3D点云上操作的代表性基线进行比较，包括L-GaN[37]、PCN[11]、3D point-Capsule Networks[25]。由于现有的所有方法都是在不同的数据集中训练的，所以我们在同一个数据集中对它们进行训练和测试，以便对它们进行定量评估。应该注意，所有方法都是以不提供标签信息的相同方式训练的。为了评估上述方法，我们使用[37，38]的评估度量。它包含两个指标：Pred→GT(预测到地面真实)误差和GT→Pred(地面真实到预测)误差。Pred→GT误差计算从预测中的每个点到其最接近的地面真实的平均平方距离。它衡量的是预测与实际情况的差别有多大。GT→Pred误差计算从地面实值中的每个点到预测中最接近的点的平均平方距离。其指示预测形状覆盖地面真实表面的程度。我们首先通过将网络的预测结果与输入的部分点云进行拼接，计算出整个点云的Pred→GT误差和GT→Pred误差。
  表1显示了结果。我们的方法在Pred→GT和GT→Pred误差上都优于所有类别的其他方法。需要注意的是，整体完整点云的误差来自两个部分：缺失区域的预测误差和原始局部形状的变化。由于我们的方法以局部形状作为输入，只输出缺失区域，所以不会改变原始的局部形状。为了确保我们的评估是合理的，我们还计算了缺失区域的Pred→GT误差和GT→Pred误差。表2显示了结果。在Pred→GT错误和GT→Pred错误上，我们的方法在13个类别中的12个类别上都优于现有的方法。此外，就所有13个类别的平均值而言，我们的方法在这两个指标上都有相当大的优势。表1和表2中的结果表明，我们的方法可以生成更高精度的点云，而在整体点云和缺失区域点云中的扭曲都较小。
  在图6中，我们可视化了由上述方法生成的输出点云。它们都来自测试集。与其他方法相比，我们的PF-Net预测具有很强的空间连续性、较高的恢复率和较小的类失真。[13]。

4.3.PF-Net的定量评估

  鉴别器分析鉴别器的功能是将预测的形状与缺失区域的真实轮廓区分开来，并优化我们的网络以生成更“真实”的配置。表1和表2显示了不带鉴别器的PF-Net的结果。与不带鉴别器的PF-Net相比，带鉴别器的PF-Net在表1和表2的Pred→GT误差的13个类别中有10个表现优于PF-Net。此外，PF-Net在表1和表2的Pred→GT误差的平均值方面都有相当大的差距。结果表明，PF-Net可以帮助最小化Pred→GT误差。如上所述，Pred→GT误差衡量预测与地面事实的差异有多大。因此，鉴别器使得PF-Net能够生成更接近地面真实的点云。

表1.整体点云的点云补全结果。训练数据包括13类不同对象[36]。显示的数字是[Pred→GT error/GT→Pred error]，比例为1,000。我们计算所有类别的平均值，并在表的最后一行显示它们。PF-Net(vanilla)是不带鉴别器的PF-Net。

表2.缺失点云的点云补全结果。显示的数字是[Pred→GT error/GT→Pred error]，比例为1,000。在此表中，我们计算缺少的点云区域中的这两个指标。

  MRE和PPD的分析为了证明CMLP的有效性，我们在ModelNet40[39]上训练了CMLP和其他遵循相同线性分类模型的提取器，并在测试集上评估了它们的总体分类精度。结果如表3所示。PointNet-MLP与没有TransformNet的PointNet具有相同的参数[10]。PointNet-CMLP用CMLP取代PointNet-MLP的MLP。Our-CMLP表现出最好的性能。结果还表明，CMLP对语义信息有更好的理解。
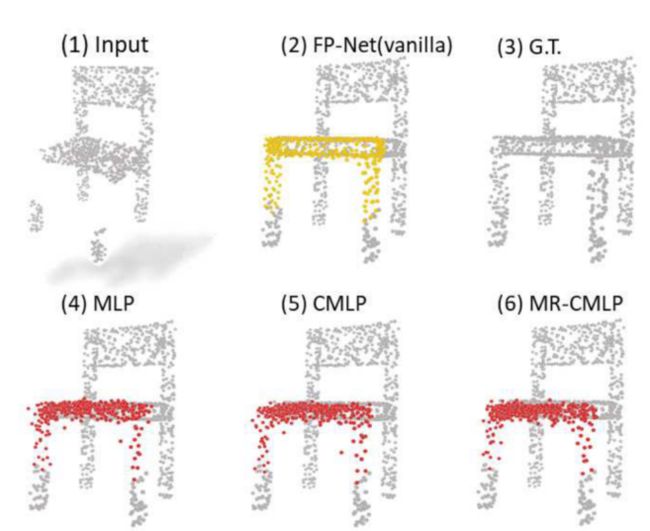
  为了评估多分辨率编码器(MRE)和点金字塔解码器(PPD)的有效性，我们进一步比较了我们的PF-Net(VANILA)与三种不同的基线：单分辨率MLP、单分辨率CMLP和多分辨率CMLP。上述方法都是以残缺的点云作为输入，输出缺失的点云。我们在“椅子”和“桌子”类中的模型上进行了实验，这两个类是我们生成的数据集中最大的两个类别。“椅子”有2658个用于训练的形状和704个用于测试的形状。“桌子”有3835个用于训练的形状和848个用于测试的形状。单分辨率MLP由5层MLP[64,128,256,512,1024]和2层线性MLP[1024,1536]组成，每层后面跟着BN和RELU激活(即，我们发现BN在这种方法中是有益的)。单分辨率CMLP的结构与单分辨率MLP相同，但MLP改为CMLP。多分辨率CMLP使用多分辨率编码器，后跟2个线性层[1024,1536]。我们计算了他们缺失点云的Pred→GT误差和GT→Pred误差。结果如表4所示。请注意，在两个类别中，CMLP和MR-CMLP在Pred→GT误差和GT→Pred误差方面均优于MLP。与MLP相比，它们的性能提升了3%到10%。然而，使用PF-Net后，Pred→GT误差和GT→Pred误差显著减小。这正是我们所期待的。由于CMLP和MR-CMLP增强了编码器提取几何和语义信息的能力，但它们的解码器只专注于生成缺失点云的整体形状。

图6.其他方法和我们的网络完成结果的比较。从上到下：输入、L-GaN[12]、PCN[11]、3D-Capsage[25]、我们的方法和地面事实。在(3)(7)中，其他方法的输出丢失了椅子和桌子下横杆的几何结构。在(3)(4)(6)中，其他方法错误地填充了G.T.的中空部分(即(3)(6)，椅背；(4)桌面下的空间被错误地填充)。在(8)中，其他人无法生成合理的形状。与之相对应的是，我们的算法能够准确地生成失真点云，失真小，复原效果好。我们的更多结果见附录。

  然而，PPD的产生过程更为顺畅。它既可以关注整体形状，也可以关注细节特征点。图7描述了“椅子”类的一个示例。
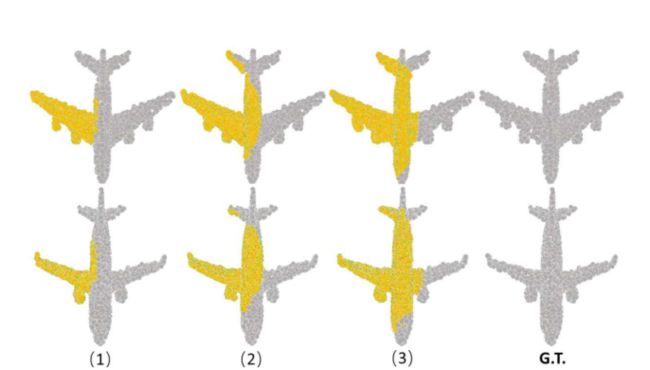
  鲁棒性测试我们在“飞机”类上进行了所有的鲁棒性测试实验。在第一个鲁棒性测试中，我们通过改变PPD中的最小值来控制网络的输出点数，并对其进行训练以修复不同程度不完全的不完整形状。实验结果如表5所示：25%、50%和75%分别表示三个不完整的输入与基本事实相比分别损失了原始点的25%、50%和75%。请注意，三个部分输入的Pred→GT误差和GT→Pred误差基本相同，这意味着我们的网络在处理具有不同缺失程度的不完整输入时具有很强的鲁棒性。图8显示了我们的网络在测试集中的性能。我们的网络准确地“识别”了不同类型的飞机，并保留了原始点云的几何细节，即使在大规模不完整的情况下也是如此。在第二个鲁棒性测试中，我们训练我们的网络来完成在不同位置丢失多个点的局部形状。图9显示了测试集中的一个例子。可以发现，PF-Net仍然能够在正确的位置预测正确的缺失点云。

表3.PointNet-MLP、PointNet-CMLP和OUR-CMLP在ModelNet40上的分类精度结果。

图7.MLP、CMLP、MR-CMLP和PF-NET(vanilla)预测的椅子。PF-Net(香草)是我们不带鉴别器的PF-Net。黄点和红点代表对PFNet(vanilla)等的预测。可以发现，G.T.的椅子中间是空心的。MLP、CMLP和MR-CMLP的预测都失去了这种详细结构。我们的PF-Net(香草)保留了这种结构，预测的噪声和失真更小。

表4。[Pred→GT error/GT→Pred error]由MLP、CMLP、MR-CMLP和我们的PF-Net(vanilla)给出。

图8.输入不同程度不完整时的修复结果示例。(1)、(2)、(3)分别丢失原始点云的25%、50%、75%的点。黄色代表预测。灰色表示未损坏的点云。

表5.。[PRED→GT ERROR/GT→PRED ERROR]由我们的PFNet给出的缺失点云。与原始点云相比，不完整点云分别损失25%、50%、75%。

图9.原始点云在两个随机位置丢失不同数量的点时的修复结果。黄色代表预测。灰色表示未损坏的点云。

5.Conclusion

  我们已经提出了一种新的方法，只使用部分点云来补全缺失的点云来完成形状。该体系结构使得网络能够在保持现有轮廓的同时，补全具有丰富语义轮廓和细节特征的目标点云。我们的方法比现有的专注于点云形状补全的方法有更好的性能。注意到，如果训练数据集足够大，我们的方法就有机会精细地修复任何复杂的随机点云。因此，可以预见，如果深入应用该方法，将会极大地提高三维识别的准确率，为自主车辆的研究和三维重建带来新的可能。

References

[1] X. Zhang, X. Le, A. Panotopoulou, E. Whiting, and C. C.Wang, “Perceptual models of preference in 3D printing direction,”ACM Trans. Graphics, vol. 34, no. 6, pp. 1–12,2015.
[2] X. Zhang, X. Le, Z. Wu, E. Whiting, and C. C. Wang, “Data-driven bending elasticity design by shell thickness,” in Computer Graphics F orum, vol. 35, no. 5, 2016, pp. 157–166.
[3] B. Zhao, X. Le, and J. Xi, “A novel sdass descriptor for fully encoding the information of a 3D local surface,”Information Sciences, vol. 483, pp. 363–382, 2019.
[4] Y . Liu, B. Fan, S. Xiang, and C. Pan, “Relation-shape convolutional neural network for point cloud analysis,”CVPR, 2019.
[5] Y . Feng, H. Y ou, Z. Zhang, R. Ji, and Y . Gao, “Hypergraph neural networks,”AAAI, 2019.
[6] T. Y u, J. Meng, and J. Y uan, “Multi-view harmonized bilinear network for 3D object recognition,”CVPR, 2018.
[7] X. He, Y . Zhou, Z. Zhou, S. Bai, and X. Bai, “Triplet-center loss for multi-view 3D object retrieval,”CVPR, 2018.
[8] A. Kanezaki, Y . Matsushita, and Y . Nishida, “RotationNet: Joint object categorization and pose estimation using multi-views from unsupervised viewpoints,”CVPR, 2018.
[9] Y . Zhou and O. Tuzel, “V oxelNet: End-to-end learning for point cloud based 3D object detection,”CVPR, 2018.
[10] C. R. Qi, H. Su, K. Mo, and L. J. Guibas, “Pointnet: Deep learning on point sets for 3D classification and segmentation,”CVPR, 2017.
[11] W. Y uan, T. Khot, D. Held, C. Mertz, and M. Hebert, “PCN: Point completion network,”3DV, 2018.
[12] P . Achlioptas, O. Diamanti, I. Mitliagkas, and L. J. Guibas, “Learning representations and generative models for 3D point clouds,”ICML, 2018.
[13] Y . Y ang, C. Feng, Y . Shen, and D. Tian, “Foldingnet: Point cloud auto-encoder via deep grid deformation,”CVPR, 2018.
[14] M. Sarmad, H. Lee, and Y . M. Kim, “RL-GAN-Net: A reinforcement learning agent controlled GAN network for realtime point cloud shape completion,”CVPR, 2019.
[15] D. Pathak, P . Krahenbuhl, J. Donahue, T. Darrell, and A. A. Efros, “Context encoders: Feature learning by inpainting,” CVPR, 2016.
[16] B. Y ang, H. Wen, S. Wang, R. Clark, A. Markham, and N. Trigoni, “3D object reconstruction from a single depth view with adversarial learning,”ICCV Workshops, 2017.
[17] A. Dai, C. R. Qi, and M. Niebner, “Shape completion using 3D-Encoder-Predictor CNNs and shape synthesis,”CVPR, 2017.
[18] W. Wang, Q. Huang, S. Y ou, C. Y ang, and U. Neumann, “Shape inpainting using 3D generative adversarial network and recurrent convolutional networks,”ICCV, 2017.
[19] C. Li, M. Zaheer, Y . Zhang, B. Poczos, and R. Salakhutdinov, “Point cloud GAN,”ICLR workshops, 2018.
[20] X. Han, . Z. Li, and . H. Huang, “High-resolution shape completion using deep neural networks for global structure and local geometry inference,” inICCV, 2017.
[21] J. Wu, C. Zhang, T. Xue, W. T. Freeman, and J. B. Tenenbaum, “Learning a probabilistic latent space of object shapes via 3D generative-adversarial modeling,”NeurIPS, 2016.
[22] Y . Y u, Z. Huang, F. Li, H. Zhang, and X. Le, “Point encoder gan: A deep learning model for 3d point cloud inpainting,” Neurocomputing, 2019.
[23] L. Y u, X. Li, C. Fu, D. Cohenor, and P . Heng, “PU-Net: Point cloud upsampling network,”CVPR, 2018.
[24] S. Sabour, N. Frosst, and G. E. Hinton, “Dynamic routing between capsules,”NeurIPS, 2017.
[25] Y . Zhao, T. Birdal, H. Deng, and F. Tombari, “3D point cap- sule networks,”CVPR, 2018.
[26] T. Y . Lin, P . Dollar, R. Girshick, K. He, B. Hariharan, and S. Belongie, “Feature pyramid networks for object detection,”CVPR, 2017.
[27] K. Chen, J. Pang, J. Wang, Y . Xiong, X. Li, S. Sun, W. Feng,Z. Liu, J. Shi, W. Ouyanget al., “Hybrid task cascade for instance segmentation,”CVPR, 2019.
[28] Z. Tian, C. Shen, H. Chen, and T. He, “Fcos: Fully convolutional one-stage object detection,”CVPR, 2019.
[29] J. Pang, K. Chen, J. Shi, H. Feng, W. Ouyang, and D. Lin, “Libra R-CNN: Towards balanced learning for object detection,”CVPR, 2019.
[30] Z. Cai and N. V asconcelos, “Cascade R-CNN: Delving into high quality object detection,”CVPR, 2018.
[31] A. Kirillov, R. Girshick, K. He, and P . Dollr, “Panoptic feature pyramid networks,”CVPR, 2019.
[32] T. Birdal and S. Ilic, “A point sampling algorithm for 3D matching of irregular geometries,”IROS, 2017.
[33] C. R. Qi, L. Yi, H. Su, and L. J. Guibas, “Pointnet++: Deep hierarchical feature learning on point sets in a metric space,” NeurIPS, 2017.
[34] H. Fan, S. Hao, and L. Guibas, “A point set generation network for 3D object reconstruction from a single image,” CVPR, 2017.
[35] I. Goodfellow, J. Pougetabadie, M. Mirza, B. Xu, D. Wardefarley, S. Ozair, A. Courville, and Y . Bengio, “Generative adversarial nets,”NeurIPS, 2014.
[36] L. Yi, V . G. Kim, D. Ceylan, I. Shen, M. Y an, H. Su, C. Lu, Q. Huang, A. Sheffer, and L. J. Guibas, “A scalable active framework for region annotation in 3D shape collections,” ACM Trans. on Graphics, vol. 35, no. 6, pp. 210:1–210:12,
2016.
[37] C. Lin, C. Kong, and S. Lucey, “Learning efficient point cloud generation for dense 3D object reconstruction,”AAAI, 2018.
[38] M. Gadelha, R. Wang, and S. Maji, “Multiresolution tree networks for 3D point cloud processing,”ECCV, 2018.
[39] Z. Wu, S. Song, A. Khosla, F. Y u, L. Zhang, X. Tang, and J. Xiao, “3D shapenets: A deep representation for volumetric shapes,”CVPR, 2015.