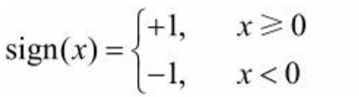李航《统计学习方法》学习笔记及python实现：第二章 感知机

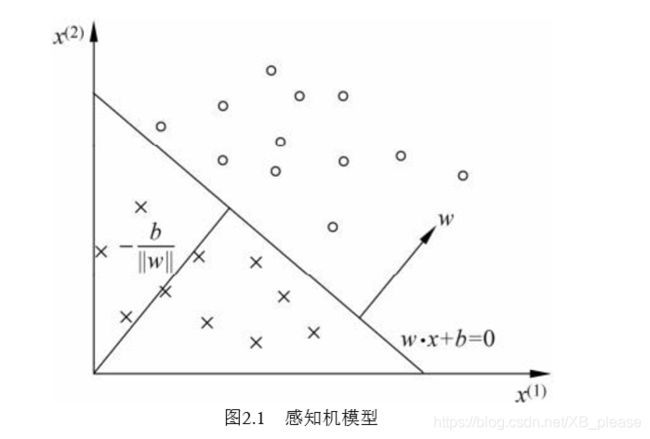
感知机（perceptron）是二类分类的线性分类模型，其输入为实例的特征向量，输出 为实例的类别，取+1和–1二值。感知机对应于输入空间（特征空间）中将实例划分为正 负两类的分离超平面，属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分 离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化， 求得感知机模型。

模型

假设输入空间（特征空间）是x⊆Rn，输出空间是 Y＝{+1,-1}。 输入x∊x表示实例的特征向量，对应于输入空间（特征空间）的点；输出y∊ Y表示实例的类别。由输入空间到输出空间的如下函数

称为感知机。
其中，w和b为感知机模型参数，w∊Rn叫作权值（weight）或权值向量 （weight vector），b∊R叫作偏置（bias），w·x表示w和x的内积。sign是符号函数，即

目标

感知机学习的目标是求得一个能够将训练集正实例点 和负实例点完全正确分开的分离超平面。

策略

定义（经验）损失函数并将损失函数极小化。

损失函数的另一个选择是误分类点到超平面S的总距离，这是感知机所采用的。

感知机sign(w·x+b)学习的损失函数定义为
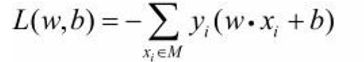其中M为误分类点的集合。这个损失函数就是感知机学习的经验风险函数。

感知机学习的策略是在假设空间中选取使损失函数式 L(w,b) 最小的模型参数w,b，即感知机模型。

算法

感知机学习问题转化为求解损失函数式 L(w,b) 的最优化问题，最优化的方法是随机梯度下降法。

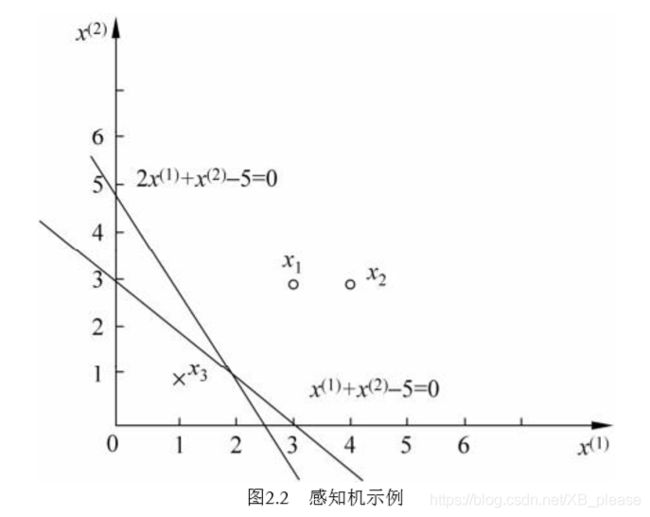
书中例题2.1

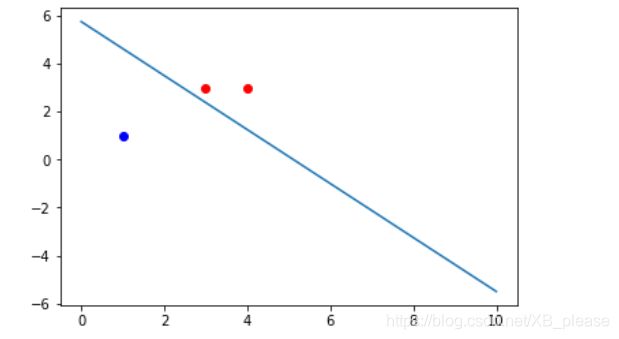
python实现

import numpy as np
import matplotlib.pyplot as plt

x = np.array([[3,3], [4,3], [1,1]])
y = np.array([1,1,-1])
plt.figure()
for i in range(len(x)):
    if y[i] == 1:
        plt.plot(x[i][0], x[i][1], 'ro')
    else:
        plt.plot(x[i][0], x[i][1], 'bo')
          
w = np.array([1,0])
b = 0
delta = 1

for i in range(100):
    choice = -1
    for j in range(len(x)):
        if y[j] != np.sign(np.dot(w,x[0]) + b):
            choice = j
            break
    if choice == -1:
        break
    w = w + delta * y[choice] * x[choice]
    b = b + delta * y[choice]

line_x = [0,10]
line_y = [0,0]

for i in range(len(line_x)):
    line_y[i] = (-w[0] * line_x[i] - b) / w[1]
    
plt.plot(line_x, line_y)
plt.savefig("picture.png")

Mnist数据集训练

此部分出处：

作者：chenxiangzhen
出处：https://www.cnblogs.com/chenxiangzhen/p/10515156.html

'''
数据集：Mnist
训练集数量：60000
测试集数量：10000
------------------------------
运行结果：
正确率：81.72%（二分类）

'''

import numpy as np
import time


def loadData(fileName):
    '''
    加载Mnist数据集
    :param fileName:要加载的数据集路径
    :return: list形式的数据集及标记
    '''
    print('start to read data')
    # 存放数据及标记的list
    dataArr = []
    labelArr = []
    # 打开文件
    fr = open(fileName, 'r')
    # 将文件按行读取
    for line in fr.readlines():
        # 对每一行数据按切割福','进行切割，返回字段列表
        curLine = line.strip().split(',')

        # Mnsit有0-9是个标记，由于是二分类任务，所以将>=5的作为1，<5为-1
        if int(curLine[0]) >= 5:
            labelArr.append(1)
        else:
            labelArr.append(-1)
        # 存放标记
        # [int(num) for num in curLine[1:]] -> 遍历每一行中除了以第一哥元素（标记）外将所有元素转换成int类型
        # [int(num)/255 for num in curLine[1:]] -> 将所有数据除255归一化(非必须步骤，可以不归一化)
        dataArr.append([int(num) / 255 for num in curLine[1:]])

    # 返回data和label
    return dataArr, labelArr


def perceptron(dataArr, labelArr, iter=50):
    '''
    感知器训练过程
    :param dataArr:训练集的数据 (list)
    :param labelArr: 训练集的标签(list)
    :param iter: 迭代次数，默认50
    :return: 训练好的w和b
    '''
    print('start to trans')
    # 将数据转换成矩阵形式（在机器学习中因为通常都是向量的运算，转换称矩阵形式方便运算）
    # 转换后的数据中每一个样本的向量都是横向的
    dataMat = np.mat(dataArr)
    # 将标签转换成矩阵，之后转置(.T为转置)。
    # 转置是因为在运算中需要单独取label中的某一个元素，如果是1xN的矩阵的话，无法用label[i]的方式读取
    # 对于只有1xN的label可以不转换成矩阵，直接label[i]即可，这里转换是为了格式上的统一
    labelMat = np.mat(labelArr).T
    # 获取数据矩阵的大小，为m*n
    m, n = np.shape(dataMat)
    # 创建初始权重w，初始值全为0。
    # np.shape(dataMat)的返回值为m，n -> np.shape(dataMat)[1])的值即为n，与
    # 样本长度保持一致
    w = np.zeros((1, np.shape(dataMat)[1]))
    # 初始化偏置b为0
    b = 0
    # 初始化步长，也就是梯度下降过程中的n，控制梯度下降速率
    h = 0.0001

    # 进行iter次迭代计算
    for k in range(iter):
        # 对于每一个样本进行梯度下降
        # 李航书中在2.3.1开头部分使用的梯度下降，是全部样本都算一遍以后，统一
        # 进行一次梯度下降
        # 在2.3.1的后半部分可以看到（例如公式2.6 2.7），求和符号没有了，此时用
        # 的是随机梯度下降，即计算一个样本就针对该样本进行一次梯度下降。
        # 两者的差异各有千秋，但较为常用的是随机梯度下降。
        for i in range(m):
            # 获取当前样本的向量
            xi = dataMat[i]
            # 获取当前样本所对应的标签
            yi = labelMat[i]
            # 判断是否是误分类样本
            # 误分类样本特诊为： -yi(w*xi+b)>=0，详细可参考书中2.2.2小节
            # 在书的公式中写的是>0，实际上如果=0，说明改点在超平面上，也是不正确的
            if -1 * yi * (w * xi.T + b) >= 0:
                # 对于误分类样本，进行梯度下降，更新w和b
                w = w + h * yi * xi
                b = b + h * yi
        # 打印训练进度
        print('Round %d:%d training' % (k, iter))

    # 返回训练完的w、b
    return w, b


def accuracy(dataArr, labelArr, w, b):
    '''
    测试准确率
    :param dataArr:测试集
    :param labelArr: 测试集标签
    :param w: 训练获得的权重w
    :param b: 训练获得的偏置b
    :return: 正确率
    '''
    print('start to test')
    # 将数据集转换为矩阵形式方便运算
    dataMat = np.mat(dataArr)
    # 将label转换为矩阵并转置，详细信息参考上文perceptron中
    # 对于这部分的解说
    labelMat = np.mat(labelArr).T

    # 获取测试数据集矩阵的大小
    m, n = np.shape(dataMat)
    # 错误样本数计数
    errorCnt = 0
    # 遍历所有测试样本
    for i in range(m):
        # 获得单个样本向量
        xi = dataMat[i]
        # 获得该样本标记
        yi = labelMat[i]
        # 获得运算结果
        result = -1 * yi * (w * xi.T + b)
        # 如果-yi(w*xi+b)>=0，说明该样本被误分类，错误样本数加一
        if result >= 0:
            errorCnt += 1
    # 正确率 = 1 - （样本分类错误数 / 样本总数）
    accruRate = 1 - (errorCnt / m)
    # 返回正确率
    return accruRate


if __name__ == '__main__':
    # 获取当前时间
    # 在文末同样获取当前时间，两时间差即为程序运行时间
    start = time.time()

    # 获取训练集及标签
    trainData, trainLabel = loadData('../Mnist/mnist_train.csv')
    # 获取测试集及标签
    testData, testLabel = loadData('../Mnist/mnist_test.csv')

    # 训练获得权重
    w, b = perceptron(trainData, trainLabel, iter=30)
    # 进行测试，获得正确率
    accruRate = accuracy(testData, testLabel, w, b)

    # 获取当前时间，作为结束时间
    end = time.time()
    # 显示正确率
    print('accuracy rate is:', accruRate)
    # 显示用时时长
    print('time span:', end - start)

运行结果

start to read data
start to read data
start to trans
Round 0:30 training
Round 1:30 training
Round 2:30 training
Round 3:30 training
Round 4:30 training
Round 5:30 training
Round 6:30 training
Round 7:30 training
Round 8:30 training
Round 9:30 training
Round 10:30 training
Round 11:30 training
Round 12:30 training
Round 13:30 training
Round 14:30 training
Round 15:30 training
Round 16:30 training
Round 17:30 training
Round 18:30 training
Round 19:30 training
Round 20:30 training
Round 21:30 training
Round 22:30 training
Round 23:30 training
Round 24:30 training
Round 25:30 training
Round 26:30 training
Round 27:30 training
Round 28:30 training
Round 29:30 training
start to test
accuracy rate is: 0.8172
time span: 2366.2143952846527