知识图谱顶会论文(ACL-2022) CAKE：用于多视图KGC的可扩展常识感知框架

CAKE：用于多视图KGC的可扩展常识感知框架

论文标题: CAKE: Scalable Commonsense-Aware Framework For Multi-View Knowledge Graph Completion
论文会议: ACL 2022
论文地址: https://arxiv.org/pdf/2202.13785.pdf

• CAKE：用于多视图知KGC的可扩展常识感知框架
  • 摘要
  • 1.引言
  • 2.相关工作
    • 2.1 KGC模型
    • 2.2 KGE的负采样
    • 2.3 常识KG
  • 3.模型方法
    • 3.1 符号和问题形式化
      • 3.1.1 常识
      • 3.1.2 KGE评价函数
      • 3.1.3 链接预测
    • 3.2 自动常识生成
    • 3.3 常识感知负采样
    • 3.4 训练KGE模型
    • 3.5 多视图链路预测

摘要

知识图不可避免地存储了大量的事实三元组，但它们仍然是不完整的。以往的知识图补全(KGC)模型仅依靠事实视图数据来预测实体之间缺失的链接，而忽略了有价值的常识知识。以往的知识图嵌入技术存在负采样无效和"事实-观点"链接预测的不确定性等问题，限制了知识图嵌入技术的性能。为了解决上述挑战，我们提出了一个新的、可扩展的常识感知知识嵌入(CAKE)框架，以自动从具有实体概念的事实三元组中提取常识。产生的常识增强了有效的自我监督，以促进高质量的负采样(NS)和联合常识和"事实-观点"链接预测。在KGC任务上的实验结果表明，我们的框架可以提高原有KGE模型的性能，并且所提出的常识感知NS模块优于其他NS技术。此外，我们提出的框架可以很容易地适应各种KGE模型，并解释预测结果。

1.引言

近年来，Freebase、DBpedia和NELL等KG已广泛应用于许多知识密集型应用，包括问答、对话系统和推荐系统。然而，手工或自动构造的KG不可避免地是不完整的，需要KGC推断新的事实。
以前的KGC模型可以分为三类：

1. 基于规则学习的模型：用于挖掘归纳推理的逻辑规则，如AMIE+、DRUM和AnyBurl。
2. 基于路径的模型：用于搜索路径的多跳推理。
3. 基于嵌入的模型(KGE)：如TransE及其变体学习实体和关系的嵌入，为链接预测的三元组的计算置信度。

在现有的KGC模型中，KGE方法实现了更高的效率和更好的性能。具体而言，基于KGE的KGC管道方法可分为两个阶段：(1)训练时学习KGE,(2)推理时的链接预测。其中，KGE依赖于负采样的基本过程。链接预测的目的是利用学习到的KG嵌入对候选三元组的分数进行排序，从而推断出三元组中缺失的实体或关系。
然而，这两个独立的阶段都有缺点：

1. 无效负采样：所有之前的NS无法同时避免采样错误的负类三元组和低质量负类三元组。例如，给定正的三元组，如图所示，现有的NS策略可能会对损坏的三元组进行采样，这实际上是一个被忽略的正类三元组，即假负类三元组。另一方面，一些生成的负类三元组的质量太差，对于训练KGE模型没有什么意义。
   

2. "事实-观点"链接预测的不确定性：由于KG嵌入相对于符号表示的偏差，限制了KGC的准确性,仅仅根据以数据驱动方式为基础的事实进行链接预测存在不确定性。以图中的尾部实体预测(David,N个国家,?)为例。从常识的观点来看，正确的尾部实体应该属于“国家”这个概念。然而，通过计算候选KG嵌入的三元组的置信度，与常识不一致的实体California甚至排名最高。
   

最后不能不提，尽管一些KGE方法利用了外部信息，包括实体类型、文本描述和实体图像。这样的辅助信息并不能提供常识的语义,它是很难获得并增强实体单一表示的。然而，有价值的常识总是通过昂贵的手工标注获得的，它的高成本导致相对较低的覆盖率。此外，现有的大型常识KG(如ConceptNet)只包含概念，没有到相应实体的链接，这导致它们不适用于KGC任务。

为了应对上述挑战，我们提出了一个新颖且可扩展的常识感知知识嵌入(CAKE)框架，以改进KGE训练中的负采样，并通过常识的自我监督提高KGC的性能。具体来说，我们尝试通过实例抽象技术自动构建明确的常识。然后，与随机采样相反，我们利用常识和复杂关系的特点，有目的地生成高质量的负类三元组。此外，还进行了多视图链接预测，以确定属于常识视图中正确概念的候选实体，并从事实的角度预测学习到的KG嵌入的答案实体。总之，我们工作的贡献有三方面：

1. 我们提出了一个具有自动常识生成机制的可扩展KGC框架，以从事实三元组和实体概念中提取有价值的常识。
2. 我们开发了一种常识性负采样策略，用于生成有效且高质量的负类三元组。同时，为了提高KGC的准确性，提出了一种多视图链接预测机制。
3. 对四个基准数据集的大量实验表明了我们整个框架和每个模块的有效性和可扩展性。本文的源代码和数据集可以在https://github.com/ngl567/cake获取

2.相关工作

2.1 KGC模型

现有的KGC模型可分为三大类：

1. 基于规则学习的算法：如AMIE+、DRUM和AnyBurl，基于规则学习的算法自动从KG中挖掘逻辑规则，并将这些规则应用于归纳链接预测。然而，由于耗时的规则搜索和评估，这些模型效率低下。
2. 基于路径的模型：基于路径的模型对连接头部和尾部实体的路径进行搜索，包括路径排序方法和基于强化学习的模型。然而，基于路径的多跳模型在路径搜索方面也花费了大量时间。
3. 基于嵌入的模型(KGE)：例如TransE、RESCAL、CompleEx、RotatE和HAKE，KGE通过学习实体和关系的嵌入，以计算三元组的置信度，从而有效预测缺失的三元组。

与当前的其他KGC方法相比，KGE上实现了更高的效率和更好的性能。然而，嵌入的天然不确定性限制了仅依靠事实的KGC的正确率。更具体地说，模型通常需要一个初始的负采样程序，随机或有目的地采样一些在KG中没有观察到的三元组并作为负类三元组，然后把它们用于训练。

2.2 KGE的负采样

遵循局部封闭世界假设(一种处理含否定词的演绎数据库查询语句的方法。可抽象成如下非单调推理机制：在封闭世界中若不知道某命题是否为真，则认定此命题为假)，现有的负采样(NS)技术可分为五类：

1. 随机均匀采样：大多数模型通过随机替换均匀分布的正类三元组中的实体或关系来生成负类三元组。
2. 基于对抗的采样：KBGAN将模型与Softmax概率相结合，在对抗网络中选择高质量的负类三元组。自我对抗采样的表现类似于KBGAN，但它利用了自我评分功能，没有生成器。
3. 基于域的采样：基于域的NS和类型约束NS都利用域或类型约束对属于正确域的损坏实体进行采样。
4. 高效采样：NSCaching使用包含候选负类三元组的缓存来提高采样效率。
5. 无采样：NS-KGE通过将损失函数转换成统一的平方损失，消除了负采样过程。

然而，所有先前的NS算法都不能解决假负类三元组的问题，因为这些NS技术(除了无采样方法之外)都将试图以更高的概率对损坏的三元组进行采样，而它们可能是正确的，只是在KG中缺失了。
基于领域的负采样严重依赖于单一类型的约束，而不是常识，这限制了负类三元组的多样性。KBGAN在负采样框架中引入了生成对抗网络(GAN),使得原始模型更加复杂和难以训练。无采样消除了负类三元组，并且必须将每个原始KGE模型都转换成平方损失，这削弱了KGE模型的性能。负采样策略的这些缺点降低了KGE的训练水平，进一步限制了KGC的表现。

2.3 常识KG

与事实三元组不同，常识可以为知识体系注入丰富的抽象知识。然而，由于手工标注成本高昂，有价值的常识很难获得。近年来，许多研究试图构建通用的常识图，如ConceptNet、Microsoft Concept Graph和ATOMIC。然而，这些常识性图只包含概念，而没有到相应实体的链接，这导致它们不适用于KGC任务。另一方面，虽然一些KGE模型(如JOIE)采用了大多数KGs内置的本体(如NELL和DBpedia)，但本体中的关系如isA、partOf和relatedTo主要代表类型层次而不是明确的常识。这种关系对于KGC是无用的，因为本体关系和事实关系之间很少有重叠。

3.模型方法

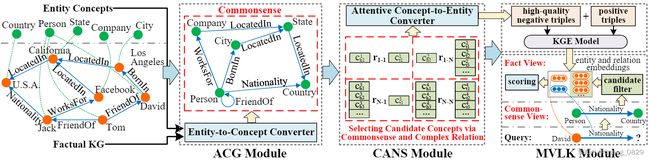
图2: CAKE框架概述。

橙色的点表示实体。绿色的点表示实体概念。

在CANS模块中，$r_{1-1},r_{1-N},r_{N-1}和r_{N-N}$分别表示1-1,1-N, N-1和N-N的各种复杂关系。

$c_{hi}^j$和$c_{ti}^j$表示第i个头概念和尾概念，它们是根据常识和特定于第j个关系的复杂关系的特征所选择的。

在本节中，我们将介绍我们最新的可扩展框架CAKE。如图2所示，整个管道由三个开发的模块组成: 自动常识生成(ACG)、常识感知负采样(CANS)模块和多视图链接预测(MVLP)模块。

1. 首先， 自动常识生成(ACG)模块(3.2节)通过实例抽象机制从具有实体概念的事实三元组中提取常识。
2. 然后， 常识感知负采样(CANS)模块(3.3节)利用生成的常识生成高质量的负类三元组，考虑到复杂关系的特征。
3. 然后， 我们的方法将正类三角和加权负类三角输入到KGE模型中，用于学习实体和关系嵌入。(3.4节)
4. 最后， 多视图链接预测(MVLP)模块 (3.5节)分两个阶段----粗预测和细预测阶段进行链接预测，从常识的角度过滤候选对象，并从事实的角度预测候选对象中使用KG嵌入的实体结果。

3.1 符号和问题形式化

3.1.1 常识

由于在理解高级语义方面的成功应用，常识获得了广泛的吸引力。高级语义通常在一些著名的常识图中表示为概念及其本体关系，如ConceptNet和Microsoft Concept Graph。值得注意的是，我们将常识扩展为两种形式:个体形式$C_1$和集合形式$C_2$。
$C_1$和$C_2$都是三元组的集合，而$C_1$中的每个三元组都是由头实体的概念$c_h$和尾实体的概念$c_t$与它们的实例级关系$r$相关联构成的，可以写成:
$$C_1=(c_h,r,c_t)\text{\hspace{1em}(1)}$$
相反，$C_2$中的每个三元组由一个关系$r$组成，连接相应的头概念集$C_h$和尾概念集$C_t$，表示为:
$$C_2=(C_h,r,C_t)\text{\hspace{1em}(2)}$$
常识生成的详细描述在3.2节中介绍。

3.1.2 KGE评价函数

由于CAKE是独立于KGE模型的可伸缩框架，所以我们可以利用任何KGE模型来学习实体和关系嵌入。因此，我们定义了一个统一符号$E(h,r,t)$来表示任意KEG模型的评价函数，以便评估三元组$(h,r,t)$的置信度。更具体地说，三种最典型的评价函数模式如下:

1. 基于翻译的评价函数，如TransE:
   $$E(h,r,t)=||h+r-t||\text{\hspace{1em}(3)}$$
   其中h、r和t分别表示头实体h、关系r和尾实体t的嵌入。
2. 基于旋转的评价函数，如RotatE:
   $$E(h,r,t)=||h◦r-t||\text{\hspace{1em}(4)}$$
   其中◦表示哈密尔顿积。
3. 基于张量分解的评价函数，如DistMult:
   $$E(h,r,t)=h^{T}diag(M_r)t\text{\hspace{1em}(5)}$$
   其中$diag(M_r)$表示关系r的对角矩阵。

3.1.3 链接预测

按照大多数之前的KGC模型，我们将链路预测视为一个实体预测任务。给定一个缺少实体(h,r,?)或(?,r,t)，链接预测将每个实体作为候选。该算法利用学习到的KGE和评价函数计算出每个候选对象的置信度分数。然后，我们根据候选实体的分数对它们进行排名，并输出前n个实体作为结果。

3.2 自动常识生成

根据3.1.1节中定义的常识表示，我们的方法理论上可以从任何KG自动生成常识，只要KG中存在一些链接到实体上的概念。
具体地说，我们开发了一个“实体到概念”的转换器，将每个事实三元组中的实体替换为相应的概念。同时，常识上的关系包含事实KGs中的实例级关系。以图2为例，事实三元组 (David,Nationality,USA) 可以转换为概念级三元组 (Person,Nationality,Country) 。特别是，个体形式$C_1$中的常识是通过消除重复的概念级三元组来实现的。然后，我们将包含相同关系的概念级三元组合并到集合中，以便用集合形式$C_2$构造常识。

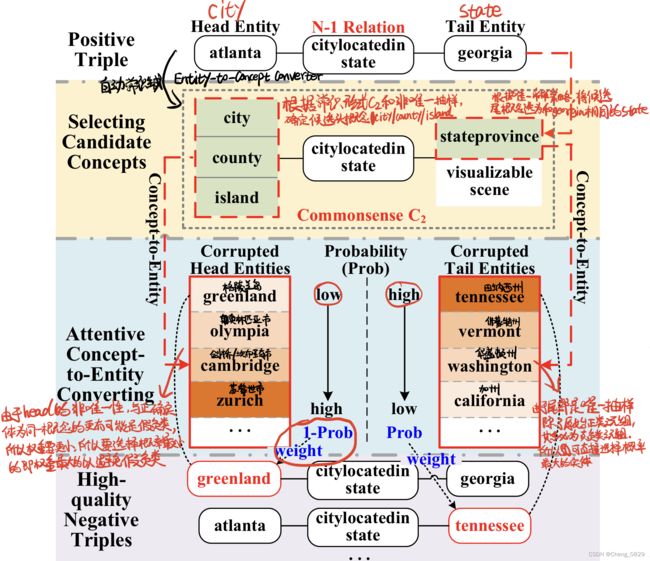
图2: CAKE框架概述：事实KG -> 自动常识生成 -> 常识感知负采样 -> 多视图链路预测

橙色的点表示实体。绿色的点表示实体概念。

在CANS模块中，$r_{1-1},r_{1-N},r_{N-1}和r_{N-N}$分别表示1-1,1-N, N-1和N-N的各种复杂关系。

$c_{hi}^j$和$c_{ti}^j$表示第i个头概念和尾概念，它们是根据常识和特定于第j个关系的复杂关系的特征所选择的。

3.3 常识感知负采样

直觉上，满足常识的负类三元组更难与正类三元组区分开来，从而产生更有效的训练信号。因此，我们尝试对符合常识的负类三元组进行采样。

为了减少假负类三元组，我们利用TransH中定义的复杂关系的特征，即利用1-1、1-N、N-1和N-N进行负采样，其中1表示当给定关系和另一个实体时，实体是唯一的，相反，N表示在这种情况下可能存在多个实体(即非唯一实体)。基于这一观察，提出了两种具体的抽样策略：

1. 唯一抽样：就破坏一个唯一实体(如N-1关系的尾部实体)而言，除了原始的正类三元组之外，被破坏的三元组肯定是实际的负类三元组。此外，与正确实体共享至少一个概念的被破坏实体被视为高质量的负类三元组，这有助于获得更一致的训练信号。抽样时尽量选择概率最大的即权重最大的尾实体,以提高质量
2. 非唯一采样：对于非唯一实体(如由N-1关系连接的头部实体)的破坏，由于头部实体的非唯一性，与正确实体属于同一概念的实体更容易为假负类。因此，在训练中，这些被判定为假负类的三元组的权重应尽可能低。同时，我们尝试对符合C2形式常识的三元组进行高质量的抽样(即尽量选择概率最小的即权重最大的头实体,以避免假负类)。

在头实体的选择(即非唯一采样)中,权重与(1-概率)成正比; 在尾实体的选择(即唯一采样)中,权重与概率成正比

图3：常识感知负采样(CANS)模块生成包含N-1关系的高质量负类三元组的示例。

为了更好地理解，图3显示了一个生成具有N-1关系的高质量负三元组的示例。整个NS过程可以分为两个步骤:

• Step 1：选取符合C2形式常识的候选概念。根据常识形式C2和非唯一抽样确定候选的头概念 city、county和island。此外，根据唯一性抽样策略将候选的尾概念选择为与Georgia相同的概念stateprovince。
• Step 2：关注的概念到实体的转换(Attentive Concept-to-Entity Converting)。为了减少假负类，同时保证负类三元组的高质量，属于候选概念的被破坏实体从以下分布中采样：

$$\begin{array}{rl}w(h_j^{{}^{\prime }},r,t)& =1-p((h_j^{{}^{\prime }},r,t)|\{(h_i,r_i,t_i)\})\\ & =1-\frac{exp\alpha E(h_j^{{}^{\prime }},r,t)}{{\sum }_{i}exp\alpha E(h_i^{{}^{\prime }},r,t)}\end{array}\text{\hspace{1em}(6)}$$

$$\begin{array}{rl}w(h,r,t_j^{{}^{\prime }})& =p((h,r,t_j^{{}^{\prime }})|\{(h_i,r_i,t_i)\})\\ & =\frac{exp\alpha E(h,r,t_j^{{}^{\prime }})}{{\sum }_{i}exp\alpha E(h,r,t_i^{{}^{\prime }})}\end{array}\text{\hspace{1em}(7)}$$

其中$h_i^{{}^{\prime }}$和$t_i^{{}^{\prime }}$分别是通过非唯一采样和唯一采样得到的被破坏的头实体和尾实体。w和p分别表示负三重的权重和概率。α为自对抗采样所激发的采样温度。

值得注意的是，考虑到概率较高的三元组更有可能是正类三元组，包含被破坏的头部实体的负类三元组的权重按照等式6定义，以防止假负类的问题。此外，包含有较高概率被破坏的尾实体的负类三元组被赋予了较高质量负类三元组的权值,这是因为它们不太可能存在假负类问题。因此，选择具有高权重的被破坏的头实体greenland和尾实体tennessee,用于生成高质量的负类三元组。

3.4 训练KGE模型

基于CANS得到的负类三元组，训练KGE模型学习实体和关系嵌入，扩大正类三元组和高质量负类三元组之间的分数差距。在本研究中，我们采用以下损失函数作为优化目标:
$$\begin{array}{rl}L=& -log\sigma (\gamma -E(h,r,t))\\ & -\sum _i^{n}0.5[w(h_i^{{}^{\prime }},r,t)log\sigma (E(h_i^{{}^{\prime }},r,t)-\gamma )]\\ & +w(h,r,t_i^{{}^{\prime }})log\sigma (E(h,r,t_i^{{}^{\prime }})-\gamma )\end{array}\text{\hspace{1em}(8)}$$
其中γ是决策边界，$[x{]}_{+}$表示0和x之间较大的值，σ为sigmoid函数。

3.5 多视图链路预测

得益于常识与事实的相同关系，常识可以直接为链接预测结果提供一个确定的范围。因此，我们在从粗到细的范式中开发了一种新的多视图链接预(MVLK)机制，以便预测更有可能的结果。

1. 在粗预测阶段，从测常识的角度挑选出候选实体;具体来说，以查询$(h,r,?)$为例，使用常识$C_1$过滤尾实体的合理概念。尾实体的候选概念集被定义为:
   $$C_{1t}=\{c_{ti}|(c_{hi},r,c_{ti})\in C_1\}\text{\hspace{1em}(9)}$$

   其中$c_{hi}$为h的第i个概念，$c_{ti}$为常识$(c_{hi},r,c_{hi})$中的尾概念。

   然后，可以确定属于概念集$C_{1t}$的实体为候选实体，因为它们满足常识，而且从常识的角度来看，它们比其他实体更有可能是正确的尾实体。

2. 在细预测阶段，我们从事实的角度对粗预测阶段派生的每个候选实体$e_i$按照如下公式打分：
   $$score(e_i)=E(h,r,e_i)\text{\hspace{1em}(10)}$$

   其中$E(h,r,e_i)$为训练KGE模型所用的评分函数。

   随后，预测结果将候选实体的分数按升序排列，并输出排名较高的实体。