优达学城《DeepLearning》2-3:权重初始化
目录
初始重量并观察训练损失
数据集和模型
导入库并加载数据
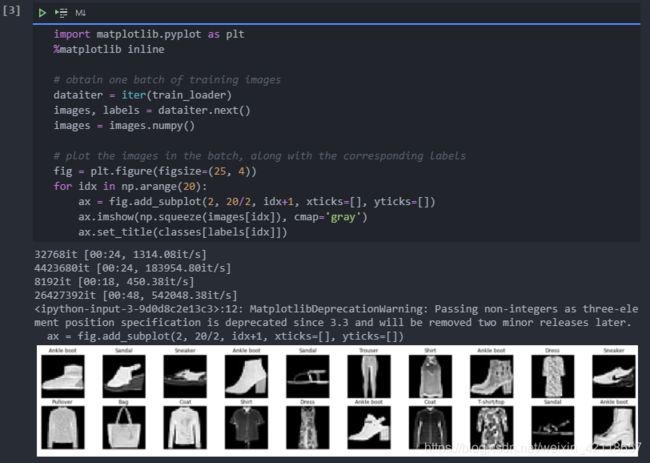
可视化一些训练数据
定义模型结构
初始化权重
全部为0或1
比较模型行为
均匀分布
统一初始化,基线
设置权重的一般规则
正态分布(Normal Distribution)
自动初始化
在本课中,您将学习如何为神经网络找到好的初始权重。权重初始化只发生一次,即在创建模型时和训练之前。具有良好的初始权值可以使神经网络接近最优解。这使得神经网络能够更快地得到最佳解。
初始重量并观察训练损失
为了了解不同权重的性能,我们将在相同的数据集和神经网络上进行测试。
我们将用不同的初始权重实例化至少两个相同的模型,并查看训练损失如何随着时间的推移而减少,如下面的示例所示。
有时训练损失的差异随着时间的推移,会很大,而其他时候,某些权重只提供小的改善。
数据集和模型
我们将训练一个MLP来对Fashion-MNIST database 中的图像进行分类,以演示不同初始权重的效果。作为提醒,FashionMNIST数据集包含服装类型的图像:classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']。对图像进行归一化,使其像素值在[0.0 - 1.0]范围内。运行下面的单元格下载并加载数据集。
导入库并加载数据
import torch
import numpy as np
from torchvision import datasets
import torchvision.transforms as transforms
from torch.utils.data.sampler import SubsetRandomSampler
# number of subprocesses to use for data loading
num_workers = 0
# how many samples per batch to load
batch_size = 100
# percentage of training set to use as validation
valid_size = 0.2
# convert data to torch.FloatTensor
transform = transforms.ToTensor()
# choose the training and test datasets
train_data = datasets.FashionMNIST(root='data', train=True,
download=True, transform=transform)
test_data = datasets.FashionMNIST(root='data', train=False,
download=True, transform=transform)
# obtain training indices that will be used for validation
num_train = len(train_data)
indices = list(range(num_train))
np.random.shuffle(indices)
split = int(np.floor(valid_size * num_train))
train_idx, valid_idx = indices[split:], indices[:split]
# define samplers for obtaining training and validation batches
train_sampler = SubsetRandomSampler(train_idx)
valid_sampler = SubsetRandomSampler(valid_idx)
# prepare data loaders (combine dataset and sampler)
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=train_sampler, num_workers=num_workers)
valid_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
sampler=valid_sampler, num_workers=num_workers)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers)
# specify the image classes
classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']可视化一些训练数据
定义模型结构
我们已经定义了用于对数据集进行分类的MLP。
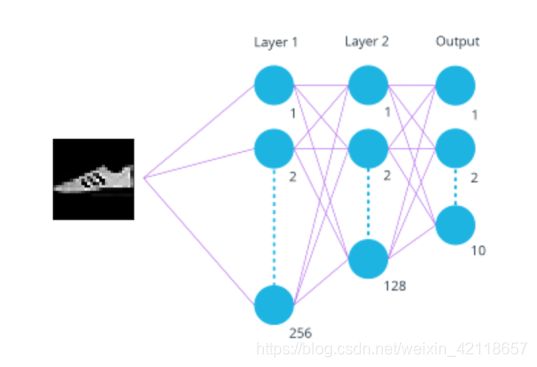
一个3层MLP,隐藏层单元数为256和128。
该MLP接受一个扁平图像(784个值的长向量)作为输入,并产生10个类分数作为输出。
我们将用ReLU激活和Adam优化器测试不同初始权重对这3层神经网络的影响。
你学到的经验教训适用于其他神经网络,包括不同的激活和优化。
初始化权重
让我们开始看一些初始权重。
全部为0或1
如果你遵循Occam剃须刀原理,你可能会认为将所有的权重设置为0或1是最好的解决方案。事实并非如此。
在权重都相同的情况下,每一层的所有神经元都产生相同的输出。这使得很难决定要调整哪些权重。
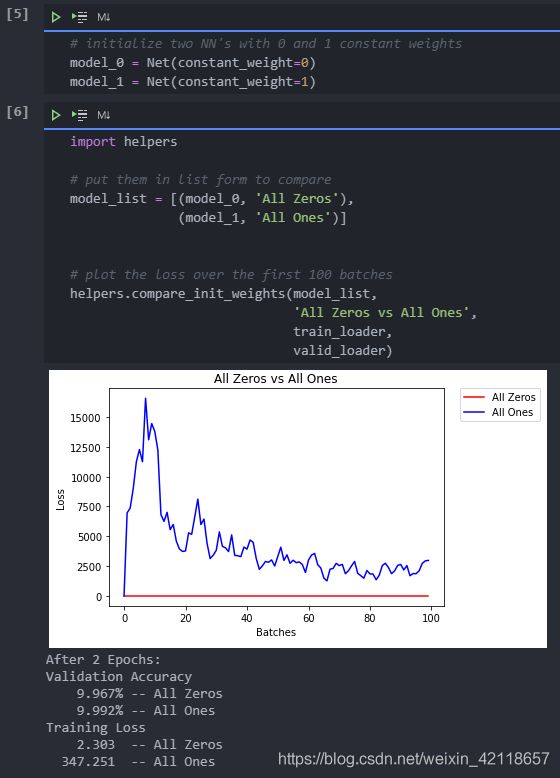
让我们通过定义两个具有这些恒定权重的模型来比较所有1和所有0权重的损失。
下面,我们使用PyTorch的nn.init初始化每个线性层,使其具有恒定的权重。init库提供了许多权重初始化函数,使您能够根据层类型初始化每个层的权重。
在下面的例子中,我们查看模型中的每个层/模块。如果它是一个线性层(因为这三个层都是针对MLP的),那么我们使用以下代码将这些层权重初始化为constant_weight,偏差为0:
constant_weight是在实例化模型时可以传入的值。
import torch.nn as nn
import torch.nn.functional as F
# define the NN architecture
class Net(nn.Module):
def __init__(self, hidden_1=256, hidden_2=128, constant_weight=None):
super(Net, self).__init__()
# linear layer (784 -> hidden_1)
self.fc1 = nn.Linear(28 * 28, hidden_1)
# linear layer (hidden_1 -> hidden_2)
self.fc2 = nn.Linear(hidden_1, hidden_2)
# linear layer (hidden_2 -> 10)
self.fc3 = nn.Linear(hidden_2, 10)
# dropout layer (p=0.2)
self.dropout = nn.Dropout(0.2)
# initialize the weights to a specified, constant value
if(constant_weight is not None):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.constant_(m.weight, constant_weight)
nn.init.constant_(m.bias, 0)
def forward(self, x):
# flatten image input
x = x.view(-1, 28 * 28)
# add hidden layer, with relu activation function
x = F.relu(self.fc1(x))
# add dropout layer
x = self.dropout(x)
# add hidden layer, with relu activation function
x = F.relu(self.fc2(x))
# add dropout layer
x = self.dropout(x)
# add output layer
x = self.fc3(x)
return x比较模型行为
下面,我们使用 helpers.compare_init_weights 来比较上面定义的两个模型(model_0和model_1)的训练和验证损失。此函数接收模型列表(每个模型具有不同的初始权重)、要生成的绘图的名称以及训练和验证数据集加载器。对于每个给定的模型,它将绘制前100批的训练损失,并打印出两个训练epoch后的验证精度。注意:如果您使用的是小批量的,您可能需要增加这里的epoch数,以便更好地比较模型在看到几百张图像后的行为。
我们绘制前100批的损失图,以便更好地判断哪些模型权重在训练开始时表现更好。我建议您查看helpers.py中的代码,以了解模型是如何训练、验证和比较的。
运行下面的单元格,查看权重全为0与权重全为1之间的差异。
helpers.py内如如下:
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim
def _get_loss_acc(model, train_loader, valid_loader):
"""
Get losses and validation accuracy of example neural network
"""
n_epochs = 2
learning_rate = 0.001
# Training loss
criterion = nn.CrossEntropyLoss()
# Optimizer
optimizer = optimizer = torch.optim.Adam(model.parameters(), learning_rate)
# Measurements used for graphing loss
loss_batch = []
for epoch in range(1, n_epochs+1):
# initialize var to monitor training loss
train_loss = 0.0
###################
# train the model #
###################
for data, target in train_loader:
# clear the gradients of all optimized variables
optimizer.zero_grad()
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# calculate the batch loss
loss = criterion(output, target)
# backward pass: compute gradient of the loss with respect to model parameters
loss.backward()
# perform a single optimization step (parameter update)
optimizer.step()
# record average batch loss
loss_batch.append(loss.item())
# after training for 2 epochs, check validation accuracy
correct = 0
total = 0
for data, target in valid_loader:
# forward pass: compute predicted outputs by passing inputs to the model
output = model(data)
# get the predicted class from the maximum class score
_, predicted = torch.max(output.data, 1)
# count up total number of correct labels
# for which the predicted and true labels are equal
total += target.size(0)
correct += (predicted == target).sum()
# calculate the accuracy
# to convert `correct` from a Tensor into a scalar, use .item()
valid_acc = correct.item() / total
# return model stats
return loss_batch, valid_acc
def compare_init_weights(
model_list,
plot_title,
train_loader,
valid_loader,
plot_n_batches=100):
"""
Plot loss and print stats of weights using an example neural network
"""
colors = ['r', 'b', 'g', 'c', 'y', 'k']
label_accs = []
label_loss = []
assert len(model_list) <= len(colors), 'Too many initial weights to plot'
for i, (model, label) in enumerate(model_list):
loss, val_acc = _get_loss_acc(model, train_loader, valid_loader)
plt.plot(loss[:plot_n_batches], colors[i], label=label)
label_accs.append((label, val_acc))
label_loss.append((label, loss[-1]))
plt.title(plot_title)
plt.xlabel('Batches')
plt.ylabel('Loss')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.show()
print('After 2 Epochs:')
print('Validation Accuracy')
for label, val_acc in label_accs:
print(' {:7.3f}% -- {}'.format(val_acc*100, label))
print('Training Loss')
for label, loss in label_loss:
print(' {:7.3f} -- {}'.format(loss, label))
def hist_dist(title, distribution_tensor, hist_range=(-4, 4)):
"""
Display histogram of values in a given distribution tensor
"""
plt.title(title)
plt.hist(distribution_tensor, np.linspace(*hist_range, num=len(distribution_tensor)//2))
plt.show()正如你所看到的,对于全0和1的权重初始化,准确率都接近于猜测,大约10%。
神经网络很难确定哪些权值需要改变,因为神经元对每一层都有相同的输出。为了避免神经元输出相同,让我们使用唯一的权重。我们还可以随机选择这些权重,以避免每次运行都陷入局部最小值。
获得这些随机权重的一个好办法是从均匀分布中取样。
均匀分布
均匀分布从一组数中选取任意数的概率相等。我们将从连续分布中挑选,因此挑选相同值的可能性很低。我们将使用NumPy的np.random.uniform函数从均匀分布中选取随机数。
np.random_uniform(low=0.0, high=1.0, size=None)- 从均匀分布输出随机值。
- 生成的值在[低,高]范围内遵循均匀分布。下限值包含在可选范围中,而上限值被排除在外。
- low:要生成的随机值范围的下限。默认为0。
- high:要生成的随机值范围的上限。默认为1。
- size:指定输出数组形状的整数或整数元组。
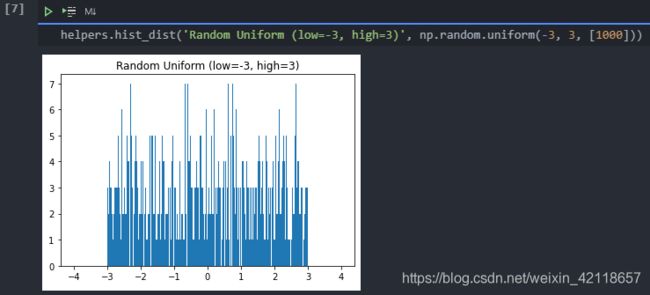
我们可以用直方图来显示均匀分布。让我们使用helper.hist_dist函数将值np.random_uniform(-3, 3, [1000])映射到直方图。这将是1000个从-3到3的随机浮点值,不包括值3。
直方图使用500个柱子来表示1000个值。因为任何一个柱子的概率都是相同的,所以每个柱子应该有2个左右的值。这正是我们看到的直方图。有些柱子有更多的,有些柱子有更少的,但他们的趋势是2左右。
现在您已经了解了统一函数,让我们使用PyTorch的nn.init将其应用于模型的初始权重。
统一初始化,基线
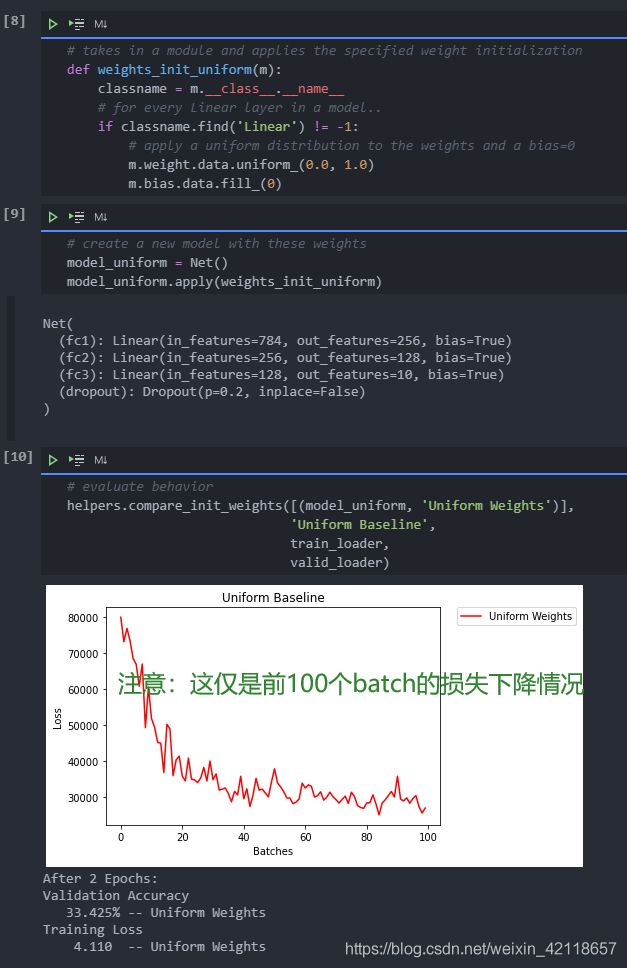
让我们看看神经网络如何使用均匀权重初始化进行训练,其中low=0.0,high=1.0。下面,我将向您展示另一种初始化网络权重的方法(除了在Net类代码中)。要在模型定义之外定义权重,你可以:
- 定义一个按网络层类型分配权重的函数,然后
- 使用model.Apply(fn)将这些权重应用于初始化的模型,该函数将函数应用于每个模型层。
这次,我们将使用weight.data.uniform直接初始化模型的权重。
损失图显示了神经网络正在学习,而不是全零或全一。我们正朝着正确的方向前进!
设置权重的一般规则
在神经网络中设置权重的一般规则是将它们设置为接近于零而不太小。
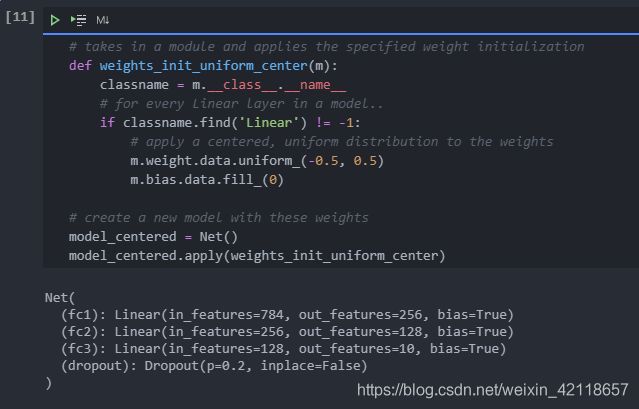
让我们看看这是否成立;让我们创建一个基线来比较,并通过将其移动0.5,使我们的统一范围居中于零之上。这将给出范围[-0.5,0.5)。
然后让我们创建一个数据分布和模型,使用一般规则进行权重初始化;使用range , where 。
最后,我们将比较这两种模型。
这种行为真的很有希望!不仅损失在减少,而且对于遵循一般规则的统一权重,似乎也很快地减少了损失;在仅仅经历了两个epoch之后,我们得到了相当高的验证准确性,这应该给你一些直觉,为什么从正确的初始权重开始,真的可以帮助你的训练!
由于均匀分布有相同的机会选择一个范围内的任何值,如果我们使用的分布有更高的机会选择接近0的数字呢?让我们看看正态分布。
正态分布(Normal Distribution)
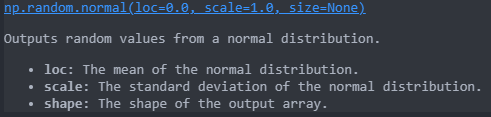
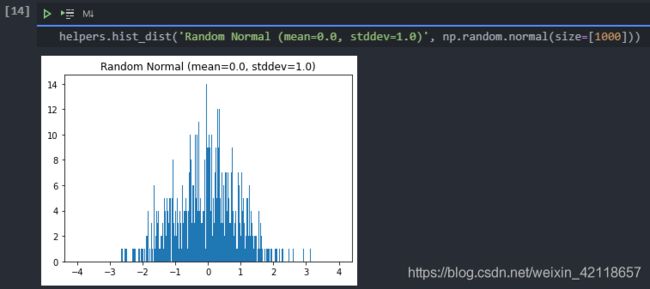
与均匀分布不同,正态分布挑选的数据具有更高接近整体均值的可能性。为了可视化,让我们将NumPy的np.random.normal函数的值绘制为直方图。
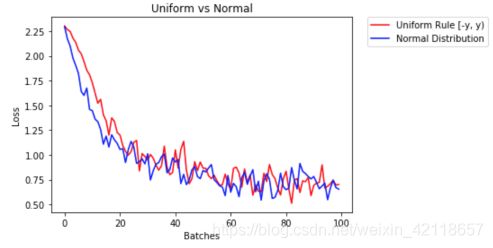
让我们将正态分布与以前基于规则的均匀分布进行比较。
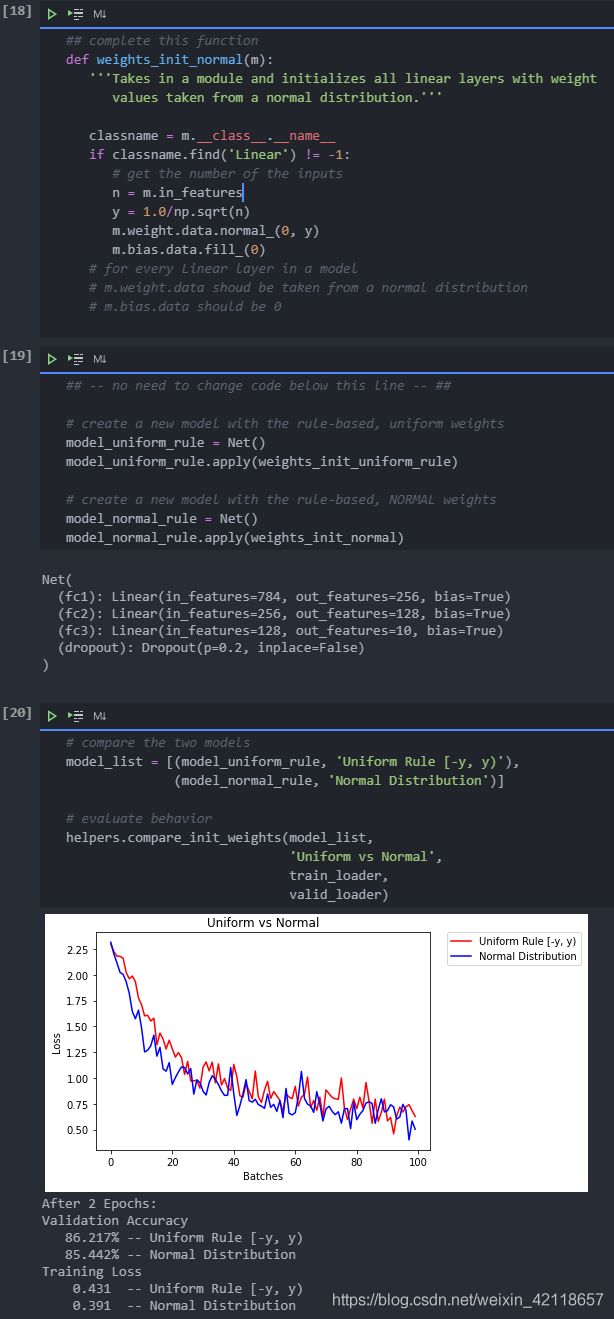
TODO:定义一个权重初始化函数,该函数从正态分布中获取权重
在这种情况下,正态分布给出了与均匀分布非常相似的行为。这可能是因为我们的网络太小了;一个较大的神经网络将从每个分布中选取更多的权值,从而放大两种初始化方式的效果。一般来说,正态分布会使模型具有更好的性能。
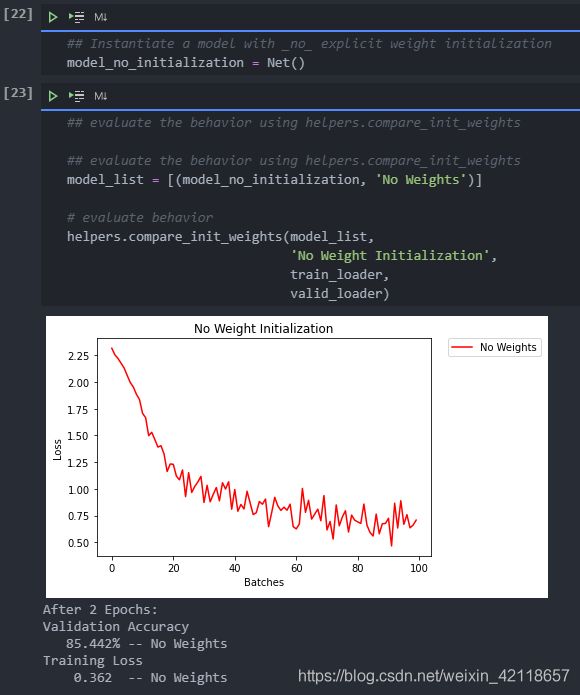
自动初始化
让我们快速看看在没有任何显式权重初始化的情况下会发生什么。
完成此练习时,请记住以下问题:
- 哪种初始化策略在两个阶段后训练损失最小?最高的验证准确度呢?
- 在测试了所有这些初始权重选项之后,您决定在最终的分类模型中使用哪一个?