第十四届蓝桥杯备赛模板题——蓝桥部队 (带权并查集)

1.蓝桥部队

1. 问题描述

小明是蓝桥部队的长官，他的班上有 $N$ 名军人和 $1$ 名军师。

这天，$N$ 名军人在操场上站成一排，起初编号为 $i$ 的军人站在第 $i$ 列。

作为长官，小明可以对军人和军师下达 $M$ 条命令，命令有两种类型，格式如下：

• 1 x y，让军人 $x$ 所在列的所有人作为一个整体移动到和军人 $y$ 所在列的后面，使两列合并为一列。
• 2 x y，询问军师军人 $x$ 和军人 $y$ 是否站在同一列。若是，则军师要回应小明 $x,y$ 之间有多少人，否则军师要回应 $-1$。
  你就是小明的军师，请你回答小明的每个询问。

2.输入格式

输入第 $1$ 行包含两个正整数 $N,M$，分别表示军人的数量和小明的命令条数。
第 $2\sim M+1$ 行每行表示一条命令。
$1\le N\le 10^5,1\le M\le 3\times 10^5，1\le x,y\le N。$

3.输入样例

3 5
2 1 2
1 2 1
2 1 2
1 1 3
2 2 3

4.样例答案

-1
0
1

5.原题连接

蓝桥部队

2.解题思路

这是一道带权并查集的模板题，将 $x$ 和 $y$ 合并到同一列和判断 $x$ 与 $y$ 是否在同一个队列中，我们可以使用朴素的并查集维护。但是题意还要求我们求出在同一列中 $x$ 与 $y$ 相距多远，这就是需要我们在使用并查集的同时维护额外的信息来帮助我们解答。使用使用数组d[]来维护每个点到其根节点的距离。如图：

1为根节点，可知 $d[1]=0$ 、$d[2]=1$ 、$d[3]=2$ 、$d[4]=3$。当询问同一列里 $x$ 和 $b$ 之间相差多少人 $s$ 时，可以得到计算公式：
$$s=abs(d[x]-d[y])-1$$
最开始每个点都是自己的根节点，所以d[]的初始化值全为 $0$ 。
首先考虑并查集核心操作之一的合并操作：

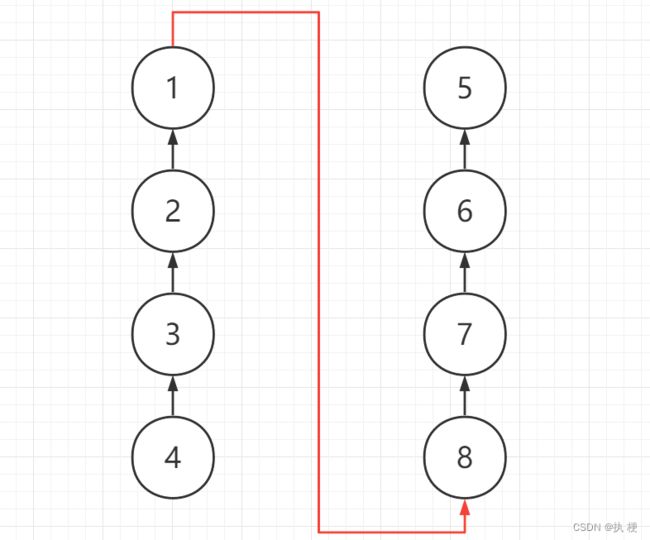
当我们将队列1接到队列5时，此时队列5中的点d[]的值无需改变，需要修改的队列1，首先考虑 $d[1]$ 会如何变化？因为1本身是根节点，所以$d[x]$的值为0，但当它接到队列5时，它就不是根节点了，那么$d[1]$的值应该更新为它到新祖宗的距离，也就是到节点5的距离，假设 $size[x]$ 为点 $x$ 所在列的元素个数，那么很明显$d[1]$的值应该更新为$size[5]$，也就是它即将接上的列的元素个数。
那么队列1中其余元素的d[]值应该如何更改呢？此时$d[2]、d[2]、d[3]$表示的还都是指向1的距离，我们应该将其更新为到5的距离，那么只需要加上1到5的距离即可。也就是到新祖宗节点的距离等于到老祖宗节点的距离加上新祖宗节点到老祖宗节点的距离。
在合并的时候考虑到效率问题，我们只需要先修改祖宗节点即可，其余的值在路径压缩，也就是在查询祖宗节点时在更新。比如上图合并时我们主要将 $d[1]$的值修改即可，对于 $234$ 我们先无需修改，再调用 $find()$ 函数查询祖宗时再同时更新。

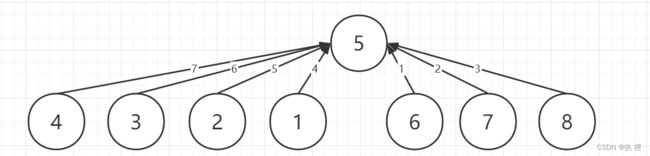
当路径压缩成功时，图将如上所示，指向根节点的值就是到根节点距离。详细的操作见代码讲解。

3.Ac_code

Java

import java.io.*;
import java.util.Arrays;

public class Main {
    static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
    static PrintWriter out=new PrintWriter(new OutputStreamWriter(System.out));
    public static void main(String[] args) throws IOException {
        String[] s=br.readLine().split(" ");
        int n=Integer.parseInt(s[0]);
        int m=Integer.parseInt(s[1]);
        UF uf=new UF(n+10);
        for (int i = 0; i < m; i++) {
            s=br.readLine().split(" ");
            int op=Integer.parseInt(s[0]);
            int x=Integer.parseInt(s[1]);
            int y=Integer.parseInt(s[2]);
            if (op==1){
                uf.merge(y,x);
            }else{
                out.println(uf.dist(x,y));
            }
        }
        out.flush();
    }
}
//带权并查集模板，可复制使用
class UF {
    int[] f, d, siz;
    //构造函数初始化并查集
    public UF(int n) {
        f = new int[n];
        d = new int[n];
        siz = new int[n];
        for (int i = 1; i < n; ++i) {
            f[i] = i;
        }
        Arrays.fill(siz, 1);
    }
    //核心操作，再查询的时候同时更新d[x]的值
    int find(int x) {
        if (x == f[x]) return f[x];
        //先记录祖宗
        int root = find(f[x]);
        //加上父亲的距离
        d[x] += d[f[x]];
        //指向祖宗
        return f[x] = root;
    }

    boolean same(int x, int y) {
        return find(x) == find(y);
    }
	//让y列接在x列的后面。
    boolean merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) return false;
        //本来d[y]等于0，现在它指向x的距离就是x的元素个数
        d[y] += siz[x];
        //此时x列的个数变多
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    int size(int x) {
        return siz[find(x)];
    }
    //查询两点之间相差几个人，不在一列返回-1
    int dist(int x, int y) {
        if (!same(x, y)) return -1;
        return Math.abs(d[x] - d[y]) - 1;
    }
}

C++

#include
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) (int)s.size();
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;

struct UF {
    std::vector<int> f, d, siz;
    UF(int n) : f(n), d(n, 0), siz(n, 1) { std::iota(f.begin(), f.end(), 0); }
    int find(int x) {
        if (x == f[x]) return f[x];
        //先记录祖宗
        int root = find(f[x]);
        //加上父亲的距离
        d[x] += d[f[x]];
        //指向祖宗
        return f[x] = root;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) return false;
        d[y] += siz[x];
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    int size(int x) { return siz[find(x)]; }
    int dist(int x, int y) {
        if (!same(x, y)) return -1;
        return abs(d[x] - d[y])-1;
    }
};
int n, m, op, x, y;
void solve()
{
    cin >> n>>m;
    UF uf(n + 10);
    for (int i = 1; i <= m; ++i)
    {
        cin >> op >> x >> y;
        if (op == 1)
        {
            uf.merge(y, x);
        } else {
            cout<<uf.dist(x,y)<<'\n';
        }
    }
}
int main()
{
    ios_base :: sync_with_stdio(false);
    cin.tie(nullptr);
    int t=1;
    while (t--)
    {
        solve();
    }
    return 0;
}