【第一周】深度学习和pytorch基础

深度学习

深度学习的缺陷

• 算法输出不稳定，容易被“攻击”
• 模型复杂度高，难以纠错和调试
• 模型层级复合程度高，参数不透明
• 端到端训练方式对数据依赖性强，模型增量性差（当样本数据量小的时候，深度学习无法体现强大拟合能力）
• 专注直观感知类问题，对开放性推理问题无能为力
• 人类知识无法有效引入进行监督，机器偏见难以避免

可解释性

2017年7月，国务院在《新一代人工智能发展规划》中提出“实现具备高可解释性、强泛化能力的人工智能”。

可解释性：

• 知道哪些特征对输出有重要影响，出了问题准确快速纠错
• 双向：算法能被人的知识体系理解 + 利用和结合人类知识
• 知识得到有效存储、积累和复用——越学越聪明

浅层神经网络

每个神经元的输出可表示为以下函数：

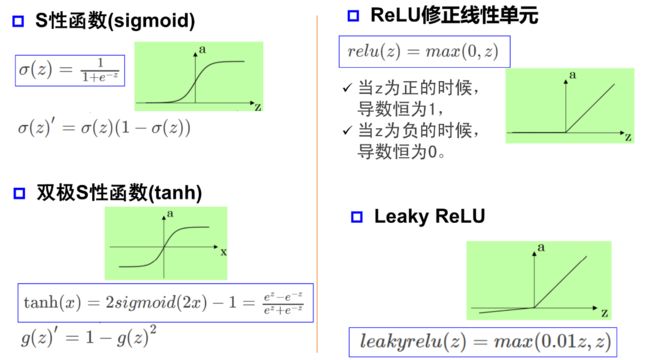
激活函数

激活函数引入非线性因素

万有逼近定理

单隐层神经网络可视化工具 —— A Neural Network Playground

如果一个隐层包含足够多的神经元，三层前馈神经网络（输入- 隐层 - 输出）能以任意精度逼近任意预定的连续函数。

当隐层足够宽时，双隐层感知器（输入 - 隐层1 - 隐层2 - 输出）可以逼近任意非连续函数：可以解决任何复杂的分类问题。

神经网络每一层的作用

神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。

每层神经网络的输出可表示为以下函数：

该函数实现了输入到输出空间的变换，其中  实现升维/降维，放大/缩小和旋转； 实现平移； 实现弯曲。

神经网络的深度与宽度

增加节点数：增加维度，即增加线性转换能力。

增加层数：增加激活函数的次数，即增加非线性转换次数

在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力：产生更多的线性区域。

深度和宽度对函数复杂度的贡献是不同的，深度的贡献是指数增长的，而宽度的贡献是线性的。

其中表示参数每层参数对函数复杂度的贡献，表示参数数量，表示深度对函数复杂度的贡献，和都是一个区间即相同的参数在不同数值下仍然有不同的复杂度。表示最大深度，表示第层。

前向传播和反向传播

局部最小值与梯度消失

假设每一层网络的输出为，其中代表第层，代表第层的输入，是激活函数，那么。在梯度下降时，参数的更新为

其中，如果此部分大于1，那么层数增多的时候，最终的求出的梯度更新将以指数形式增加，即发生梯度爆炸；如果此部分小于1，那么随着层数增多，求出的梯度更新将会以指数形式衰减，即发生了梯度消失。

解决方案：

Layer-wise Pre-train：2006年Hinton等提出的训练深度网路的方法，用无监督数据作分层预训练，再用有监督数据fine-tune（DBN, 2006）。

ReLU：新的激活函数解析性质更好，克服了sigmoid函数和tanh函数的梯度消失问题（AlexNet， 2012）。

辅助损失函数：e.g. GoogLeNet中的两个辅助损失函数，对浅层神经元直接传递梯度（Inception V1, 2013）。

Batch Normalization：逐层的尺度归一（Inception V2, 2014）。

LSTM：通过选择记忆和遗忘机制克服RNN的梯度消失问题，从而可以建模长时序列。

Pytorch

PyTorch 是一个 Python 库，它主要提供了GPU加速的张量计算 (Tensor Computation) 功能和构建在反向自动求导系统上的深度神经网络功能，使用时需导入torch包。

Pytorch使用torch.Tensor张量类定义数据，torch.autograd.Function函数类定义数据操作。

Tensor

Tensor的关键组成：

• data属性，用来存数据
• grad属性，用来存梯度
• grad_fn，用来指向创造自己的Function

定义数据

Tensor支持各种各样类型的数据，包括：

torch.float32, torch.float64, torch.float16, torch.uint8, torch.int8, torch.int16, torch.int32, torch.int64

x = torch.tensor(666)    # 一个数

x = torch.tensor([1,2,3,4,5,6])    # 一维向量

# 值全为1的任意维度的张量
# torch.ones(size=(int ...), dtype=None)
x = torch.ones(2,3)

# 对角线全1，其余部分全0的二维数组
x = torch.eye(2,3)

# 返回从start到end（不包括端点）步长为step的一维张量
# torch.arange(start=0, end, step=1)
a = torch.arange(0, 10, 2)

# 返回从start到end（包括端点）的等距的steps个数据点
# torch.linspace(start, end, steps)
b = torch.linspace(0, 10, 2)

print(a)    # tensor([0, 2, 4, 6, 8])
print(b)    # tensor([ 0., 10.])

# 从区间[0，1)的均匀分布中抽取的一组随机数
x = torch.rand(2,3)

# 从标准正态分布(均值为0，方差为1)中抽取的一组随机数
x = torch.randn(2,3)

# 基于现有的tensor，创建一个新tensor，
# 从而可以利用原有的tensor的dtype，device，size之类的属性信息
y = x.new_ones(5,3)   #tensor new_* 方法，利用原来tensor的dtype，device

定义操作

凡是用Tensor进行各种运算的，都是Function

• 基本运算，加减乘除，求幂求余
• 布尔运算，大于小于，最大最小
• 线性运算，矩阵乘法，求模，求行列式

基本运算： abs/sqrt/div/exp/fmod/pow ，一些三角函数 cos/sin/asin/atan2/cosh，其他函数 ceil/round/floor/trunc

布尔运算： gt/lt/ge/le/eq/ne, topk, sort, max/min

线性计算： trace, diag, mm/bmm，t，dot/cross，inverse，svd等

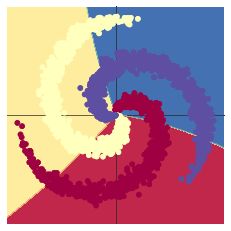
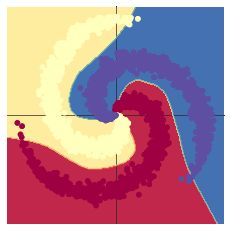
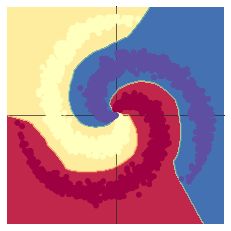
螺旋数据分类

learning_rate = 1e-3
lambda_l2 = 1e-5

# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, H2),
    nn.ReLU(),
    nn.Linear(H2, C)
)
model.to(device) # 把模型放到GPU上

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数
criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

# 开始训练
for t in range(1000):
    # 把数据输入模型，得到预测结果
    y_pred = model(X)
    # 计算损失和准确率
    loss = criterion(y_pred, Y)
    score, predicted = torch.max(y_pred, 1)
    acc = (Y == predicted).sum().float() / len(Y)
    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))
    display.clear_output(wait=True)

    # 反向传播前把梯度置 0 
    optimizer.zero_grad()
    # 反向传播优化 
    loss.backward()
    # 更新全部参数
    optimizer.step()

线性模型	Linear(in_features=2, out_features=100, bias=True) Linear(in_features=100, out_features=3, bias=True) epoch：1000 optimizer：SGD learning_rate = 1e-3	[LOSS]: 0.862976 [ACCURACY]: 0.501
两层神经网络	Linear(in_features=2, out_features=100, bias=True) Sigmoid() Linear(in_features=100, out_features=3, bias=True) epoch：1000 optimizer：Adam learning_rate = 1e-3	[LOSS]: 0.754807 [ACCURACY]: 0.509
两层神经网络	Linear(in_features=2, out_features=100, bias=True) ReLU() Linear(in_features=100, out_features=3, bias=True) epoch：1000 optimizer：Adam learning_rate = 1e-3	[LOSS]: 0.171876 [ACCURACY]: 0.955
两层神经网络	Linear(in_features=2, out_features=100, bias=True) ReLU() Linear(in_features=100, out_features=3, bias=True) epoch：1000 optimizer：SGD learning_rate = 1e-1	[LOSS]: 0.377146 [ACCURACY]: 0.813
三层神经网络	Linear(in_features=2, out_features=100, bias=True) ReLU() Linear(in_features=100, out_features=25, bias=True) ReLU() Linear(in_features=25, out_features=3, bias=True) epoch：1000 optimizer：Adam learning_rate = 1e-3	[LOSS]: 0.022764 [ACCURACY]: 0.998
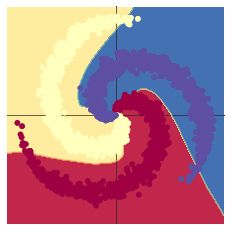
三层神经网络	Linear(in_features=2, out_features=100, bias=True) ReLU() Linear(in_features=100, out_features=25, bias=True) ReLU() Linear(in_features=25, out_features=3, bias=True) epoch：10000 optimizer：Adam learning_rate = 1e-3	[LOSS]: 0.002587 [ACCURACY]: 0.999

在10000轮训练过程中，损失函数出现先减小后增大再减小的现象。该现象可能是损失函数进入局部最小值后发生震荡，最终又跳出该局部最小值造成的。也可能是学习率过大造成震荡，在权重衰减达到合适的学习率后震荡消失。