NNDL 作业11：优化算法比较

目录

1. 编程实现图6-1，并观察特征

2. 观察梯度方向 

3. 编写代码实现算法，并可视化轨迹 

5. 总结SGD、Momentum、AdaGrad、Adam的优缺点 

6. Adam这么好，SGD是不是就用不到了？ 

参考

---

 

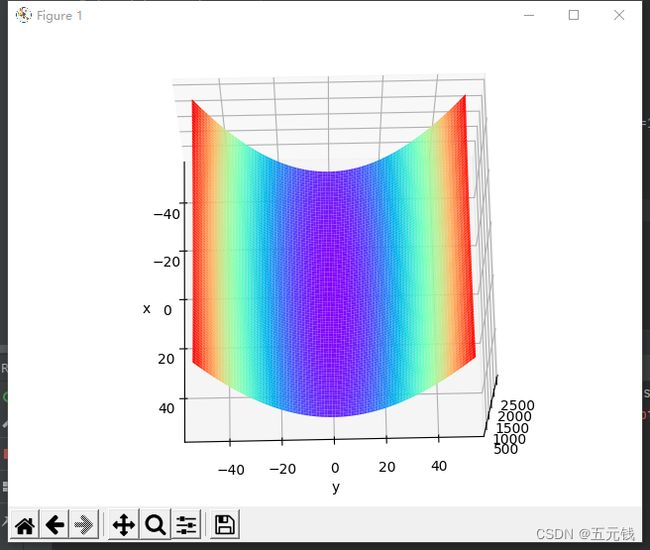
1. 编程实现图6-1，并观察特征

代码实现

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
 
 
def func(x, y):
    return x * x / 20 + y * y
 
 
def paint_loss_func():
    x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数
 
    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)
 
    fig = plt.figure()  # figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')
 
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()
 
 
paint_loss_func()

 运行结果

2. 观察梯度方向 

 

 上式表示的函数梯度如下图所示： 

由图像能够看出该函数梯度的特征为：

1. 在y轴方向的坡度大，在x轴方向的坡度小。
2. 虽然最小值在(x,y)=(0,0)处，但梯度在很多地方并没有指向(0,0)。

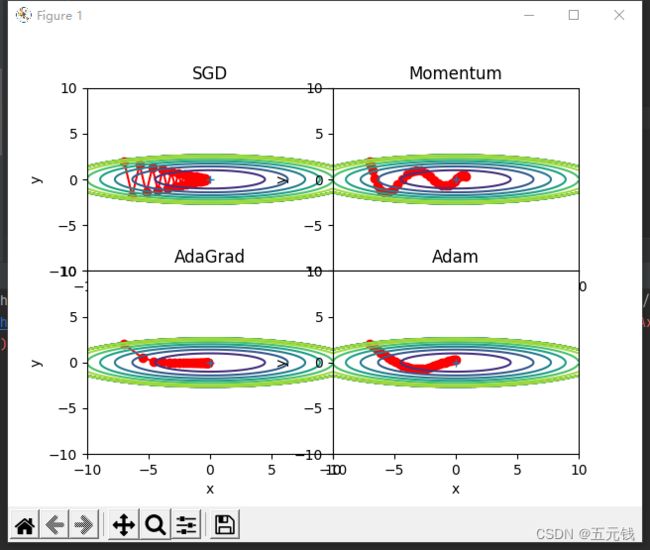
3. 编写代码实现算法，并可视化轨迹 

SGD、Momentum、Adagrad、Adam

 代码实现

import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
 
 
class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
 
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]
 
 
class Momentum:
    """Momentum SGD"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]
 
 
class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]
 
 
class AdaGrad:
    """AdaGrad"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class RMSprop:
    """RMSprop"""
 
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
 
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
 
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
 
        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
 
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
 
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
 
 
def f(x, y):
    return x ** 2 / 20.0 + y ** 2
 
 
def df(x, y):
    return x / 10.0, 2.0 * y
 
 
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
 
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
 
idx = 1
 
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
 
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
 
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
 
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
 
    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0
 
    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
 
plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

运行结果

 

 由图可以看出这四个最优化方法中AdaGrad的收敛效果最好。 

5. 总结SGD、Momentum、AdaGrad、Adam的优缺点 

SGD

优点

• 算法收敛速度快(在Batch Gradient Descent算法中, 每轮会计算很多相似样本的梯度, 这部分是冗余的)
• 可以在线更新
• 有几率跳出一个比较差的局部最优而收敛到一个更好的局部最优甚至是全局最优

缺点

• 容易收敛到局部最优，并且容易被困在鞍点

 

Momentum 

优点

• 与梯度下降相比，下降速度快，因为如果方向是一直下降的，那么速度将是之前梯度的和，所以比仅用当前梯度下降快。
• 对于窄长的等梯度图，会减轻梯度下降的震荡程度，因为考虑了当前时刻是考虑了之前的梯度方向，加快收敛。
• 增加了稳定性。
• 还有一定摆脱局部最优的能力。

缺点

• 其更新方向完全依赖于当前batch计算出的梯度，因而十分不稳定。

AdaGrad 

优点

• 不同更新频率的参数具有不同的学习率，减少摆动，在稀疏数据场景下表现会非常好；
• 允许使用一个更大的学习率α \alphaα，从而加快算法的学习速度；

缺点

• 仍需要手动设置一个全局学习率 , 如果学习率设置过大的话，会使regularizer过于敏感，对梯度的调节太大。
• 训练到中后期，分母中对历史梯度一直累加，学习率将逐渐下降至0，使得训练提前结束。
• 初始化W影响初始化梯度，如果初始梯度很大的话，会导致整个训练过程的学习率很小，导致学习时间变长。

Adam 

优点

• 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
• 对内存需求较小
• 为不同的参数计算不同的自适应学习率
• 也适用于大多非凸优化
• 适用于大数据集和高维空间

缺点

• 可能不收敛。
• 可能错过全局最优解。

6. Adam这么好，SGD是不是就用不到了？ 

不是的，如今仍然在很多领域里（如计算机视觉的对象识别、NLP中的机器翻译）的最佳成果仍然是使用带动量（Momentum）的SGD来获取到的。在计算机视觉领域，SGD时至今日还是统治级的优化器。但是在自然语言处理（特别是用Transformer-based models）领域，Adam已经是最流行的优化器了。

参考

NNDL 作业11：优化算法比较

 优化方法总结：SGD，Momentum，AdaGrad，RMSProp，Adam