全连接、卷积、循环神经网络介绍
神经网络简介
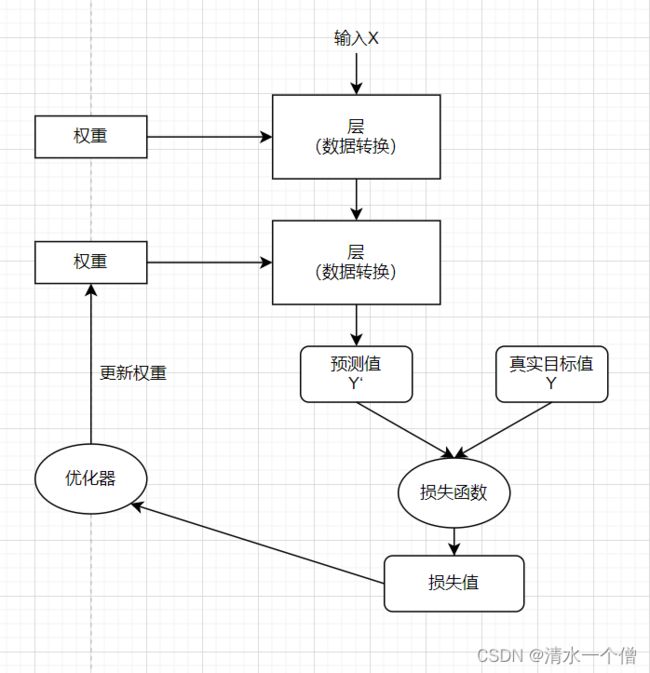
训练神经网络主要围绕下面四部分：
- 层，多个层组合成网络（或模型）
- 输入数据和相应目标
- 损失函数，即用于学习的反馈信号
- 优化器，决定学习过程如何进行
层、损失函数、优化器之间的关系：
层：神经网络中的核心组件是层，它是一种数据处理模块，可以将其看作是数据过滤器，进去一些数据，出来的数据更具代表性。层的创建原理类似于神经元，神经元模型结构为：
- x：模拟前一个神经元输入（树突）
- w：模拟“突触”，输入、记忆能力
- w0：为偏置量
- f：为激活函数，模拟神经元的兴奋和抑制
激活函数是人工神经网络的一个极其重要的特征。它决定一个神经元是否应该被激活，激活代表神经元接收的信息与给定的信息有关。激活函数对输入信息进行非线性变换。 然后将变换后的输出信息作为输入信息传给下一层神经元。
当我们不用激活函数时，权重和偏差只会进行线性变换。线性方程很简单，但解决复杂问题的能力有限。没有激活函数的神经网络实质上只是一个线性回归模型。激活函数对输入进行非线性变换，使其能够学习和执行更复杂的任务。我们希望我们的神经网络能够处理复杂任务，如语言翻译和图像分类等。线性变换永远无法执行这样的任务。
激活函数使反向传播成为可能，因为激活函数的误差梯度可以用来调整权重和偏差。如果没有可微的非线性函数，这就不可能实现。
不同的张量格式与不同的数据处理类型需要用到不同的层
- 简单的向量数据保存在形状为（samples，features）的2D张量中，通常使用密集连接层也叫全连接层，对应keras的Dense类
- 序列数据保存在形状为（samples，timesteps，features）的3D张量中，通常使用循环层，比如keras的LSTM层
- 图像数据保存在4D张量中，通常使用二维卷积层（keras的Conv2D）来处理
损失函数（目标函数）：在训练过程中需要将其最小化。它能衡量当前任务是否已经成功完成。
选择正确的目标函数对解决问题是十分重要的。网络的目的是使得损失尽可能最小化，因此如果目标函数不能与成功完成当前任务不完全相关，那么网络最终得到的结果可能会不符合预期。
对于分类、回归、序列预测等常见问题，可以遵循简单的指导原则来选取正确的损失函数
- 对于二分类问题，可以使用二元交叉熵（binary crossentropy）损失函数
- 对于多分类问题，可以使用分类交叉熵（categorical crossentropy）损失函数
- 对于回归问题，可以使用均方误差（mean-squared error）损失函数
- 对于序列学习问题，可以用联结主义时序分类（CTC，connectionist temporal classification）损失函数
优化器：决定如何基于损失函数对网络进行更新
为了得到泛化效果好的模型，需要防止神经网络过拟合
- 获得更多的训练数据
- 减小网络容量
- 添加权重正则化
- 添加dropout
权重正则化：强制让模型权重只能取较小的值，从而限制模型的复杂度，这使得权重的分布更加规则。实现方法就是向网络损失函数中添加与较大权重值相关的成本。这个成本有两种形式。
- L1 正则化（L1 regularization）：添加的成本与权重系数的绝对值［权重的 L1 范数（norm）］成正比。
- L2 正则化（L2 regularization）：添加的成本与权重系数的平方（权重的 L2 范数）成正比。
神经网络的 L2 正则化也叫权重衰减（weight decay）。不要被不同的名称搞混，权重衰减
与 L2 正则化在数学上是完全相同的。
dropout正则化：dropout是神经网络最有效也最常用的正则化方法之一，对某一层使用dropout，就是在训练过程中随机将该层的一些输出特征舍弃。
卷积神经网络
全连接网络的缺陷：
-
首先将图像展开为向量会丢失空间信息；
-
其次参数过多效率低下，训练困难；
-
同时大量的参数也很快会导致网络过拟合
- 密集连接层和卷积层的根本区别在于，Dense层从输入特征空间中学到的是全局模式（比如MNIST数字，全局模式就是涉及所有像素的模式），而卷积层学到的是局部模式，对于图像来说，学到的就是在输入图像的二维小窗口中发现的模式。
这个重要特性使得卷积神经网络具有两个特殊性质
- 卷积神经网络学习到的模式具有平移不变性。卷积神经网络在图像右下角学到某个模式之后，它可以在任何地方识别这个模式，比如左上角。对于密集链接网络来说，如果模式出现在新的位置，它只能重新学习这个模式。这使得卷积神经网络在处理图像时可以很高效利用数据（因为视觉世界从根本上具有平移不变性），它只需要较少的训练样本基于可以学习到具有泛化能力的数据表示
- 卷积神经网络可以学习到模式的空间层次结构，例如第一个卷积层学习较小的局部模式（比如边缘），第二个卷积层将学习由第一层特征组成的更大的模式，以此类推。这使得卷积神经网络可以有效地学习越来越复杂、越来越抽象的视觉概念（因为视觉世界从根本上具有空间层次结构）
卷积神经网络结构
- 输入层
- 卷积层
- 激活函数
- 池化层
- 全连接层
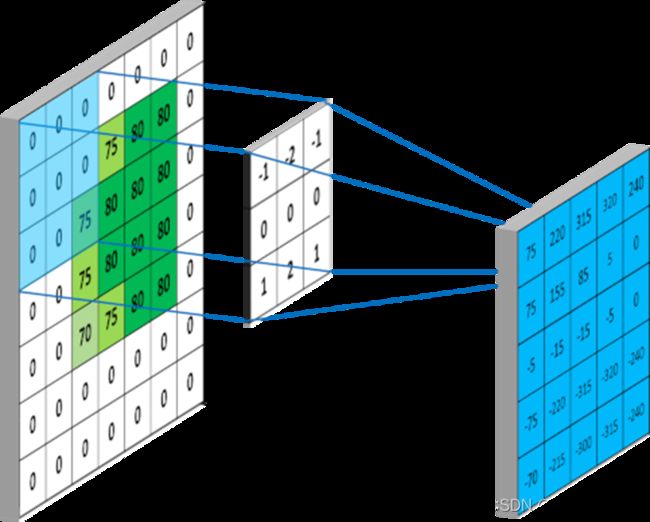
卷积层：
CNN 网络中卷积层的两个常用参数padding和strides
padding是指是否对图像的外侧进行补零操作，其取值一般为VALID和SAME两种。
- VALID表示不进行补零操作，对于输入形状为(,)(x,y)的矩阵，利用形状为(,)(m,n)的卷积核进行卷积，得到的结果矩阵的形状则为(−+1,−+1)(x-m+1,y-n+1)。
- SAME表示进行补零操作，在进行卷积操作前，会对图像的四个边缘分别向左右补充(|2)+1(m|2)+1个零。向上下补充(|2)+(n|2)+1，| 表示整除
strides是指进行卷积操作时，每次卷积核移动的步长。示例中，卷积核在横轴和纵轴方向上的移动步长均为 1，除此之外用于也可以指定不同的步长。
filters其表示在一个卷积层中使用的卷积核的个数。在一个卷积层中，一个卷积核可以学习并提取图像的一种特征，但往往图片中包含多种不同的特征信息，因此我们需要多个不同的卷积核提取不同的特征。
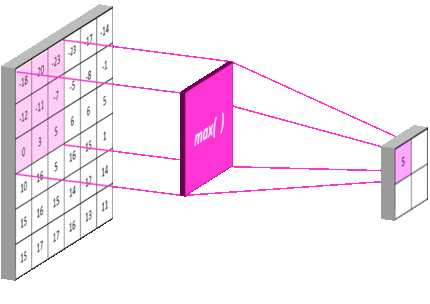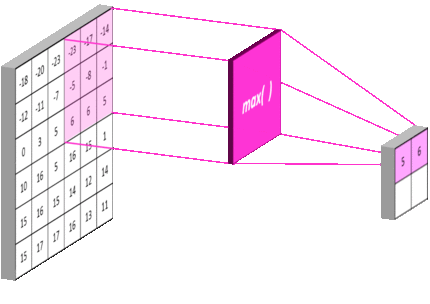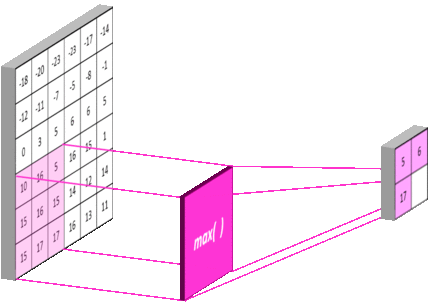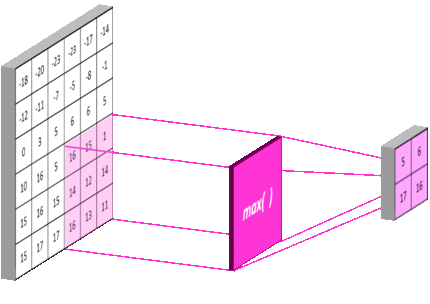
池化层：
- 池化层是一个利用池化函数(pooling function)对网络输出进行进一步调整的网络层。
- 池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。
- 常用的池化函数包括最大池化(max pooling)函数(即给出邻域内的最大值)和平均池化(average pooling)函数(即给出邻域内的平均值) 等
卷积神经网络中数据经过卷积、池化后连接全连接层，数据形状的计算方法为：
全连接层数据形状=（原始数据形状-卷积核大小）/池化核大小
例如原始数据为32×32，卷积核大小为5×5，池化函数选择最大池化函数大小为2×2
那么经过一次卷积层和池化层后数据形状为：
（32-（5-1））/2×（32-（5-1））/2=14×14
循环神经网络
CNN局限性：
- 将固定大小的向量作为输入（比如一张图片），然后输出一个固定大小的向量（比如不同分类的概率）。
- CNN还按照固定的计算步骤（比如模型中层的数量）来实现这样的输入输出。这样的神经网络没有持久性
RNN优点：
- RNN 是包含循环的网络，允许信息的持久化。
- 在自然语言处理(NLP)领域，RNN已经可以做语音识别、机器翻译、生成手写字符，以及构建强大的语言模型。
- 机器视觉领域，RNN也非常流行。包括帧级别的视频分类，图像描述，视频描述以及基于图像的Q&A等等
递归神经网络基本模型
RNN局限：因为RNN是有记忆的网络，当前输出与之前的所有状态都相关，这显然是不合适的，因为距离过远的数据之间可能关联并不大，而且这也导致了反向传播中可能出现梯度消失的情况。
- LSTM模型是用来解决simple RNN对于长时期依赖问题（Long Term Dependency），即通过之前提到的但是时间上较为久远的内容进行后续的推理和判断。
- LSTM的基本思路是引入了门控装置，来处理记忆单元的记忆/遗忘、输入程度、输出程度的问题。
- 通过一定的学习，可以学到何时对各个门开启到何种程度，因为门控也是由有一定可以学习的参数的神经网络来实现的，这样就可以让机器知道何时应该记住某个信息，而何时应该抛弃某个信息。
RNN结构：
LSTM结构：
RNN是解决了CNN不能记忆过去的问题
LSTM解决了RNN记忆太多的问题
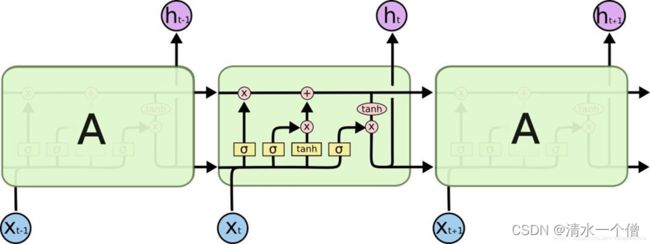
RNN结构：
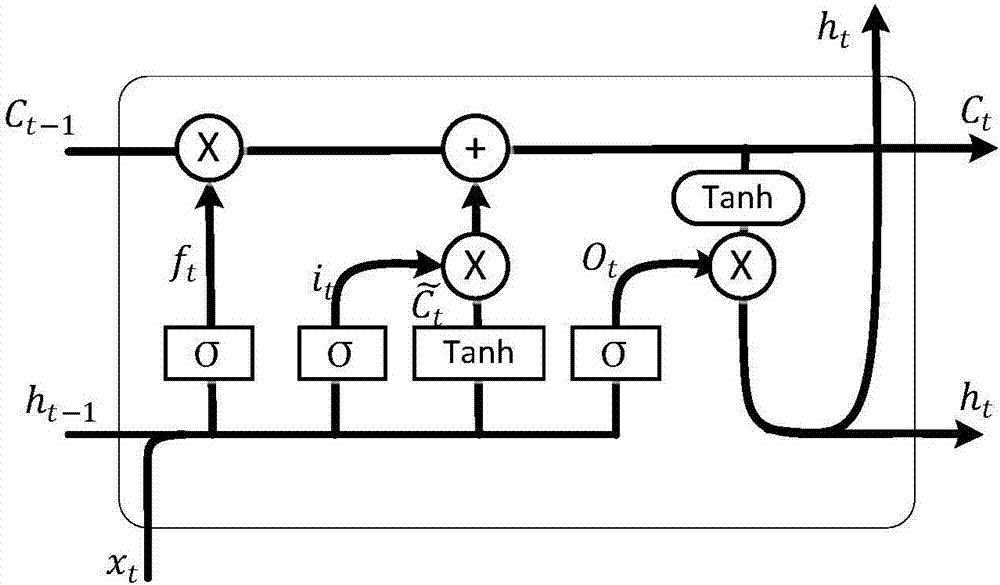
LSTM结构：
通过观察发现RNN中上一状态的一个输出作为下一状态输入（用作记忆）、LSTM中有两个输出作为下一状态输入（控制记忆和忘记）下面介绍一下是如何控制记忆和忘记的。
门是一种让信息选择式通过的方法，sigmoid神经网络层和一成法操作
C控制参数：决定什么样的信息会被保留，什么样的会被遗忘。C是网络训练得到的。
丢弃信息：
![\large f_{t}=\delta (W_{f}\cdot[h_{t-1},x_{t}]+b_{f} )](http://img.e-com-net.com/image/info8/a7ff4e33b0674c828637e349428e0f4a.gif){kind=small}
与
计算决定丢弃什么信息
保存信息：
![\large i_{t}=\delta (W_{i}\cdot [h_{t-1},x_{t}]+b_{i})](http://img.e-com-net.com/image/info8/12c33d19f7644d96a61a09b8d92c42a3.gif){kind=small}
![\bg_white \large \widetilde{C_{t}}=tanh(W_{C}\cdot [h_{t-1},x_{t}]+b_{C})](http://img.e-com-net.com/image/info8/58660f25fec948229156c647f1f55112.gif){kind=small}
要保留下来的新信息
新数据形成的控制参数
更新控制参数：
利用新的控制参数产生输出：
![o_{t}=\delta (W_{o}[h_{t-1},x_{t}]+b_{o})](http://img.e-com-net.com/image/info8/bf03cb04e91c4819a4e261caa8e644a4.gif){kind=small}
总的来说：
1路决定舍弃哪些信息
2路决定保存哪些信息
3路决定当前输出
循环神经网络的构建
不同于卷积神经网络有很详细的层次结构，每个层都有自己要实现的任务，我们根据每层的需要就可以编辑出卷积神经网络，但是循环神经网络似乎没有这种很详细的层次结构，那么循环神经网络在构建时是如何构建的呢？
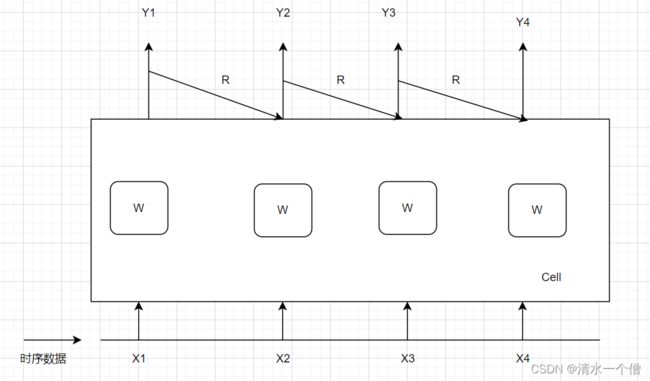
循环神经网络主要解决的是有顺序的数据结构，例如说话的顺序、文本的顺序等。
以minist数据集的分类来说，若我们想要对其进行分类的任务，那么我们要将图片看成一个有序的序列，每次输入一行的数据，共输入28次来表示一张图片。下面以代码进行介绍。
import tensorflow as tf
import numpy as np
mnist=tf.keras.datasets.mnist
(xtrain,ytrain),(xtest,ytest)=mnist.load_data()
print(xtrain.shape)
# 对数据进行归一化 对标签进行one-hot编码
xtrain=xtrain/255
ytrain=np.eye(ytrain.shape[0],10)[ytrain.T]
lr=0.001 # 学习率
training_iters=100000 # train_step上限
batch_size=128
n_inputs=28 # MNIST数据集（28×28） 分别代表一次输入一行，一个照片分28次前后输入
n_steps=28
n_hidden_units=128 # 输入cell之前的隐藏层
n_classes=10
# x y placeholder
x=tf.placeholder(tf.float32,[None,n_steps,n_inputs])
y=tf.placeholder(tf.float32,[None,n_classes])
# 输入cell之前和之后都有一个隐藏层
# 对隐藏层权重和偏置项初始值的定义
weights={
# shape(28,128)
'in':tf.Variable(tf.random_normal([n_inputs,n_hidden_units])),
# shape(128,10)
'out':tf.Variable(tf.random_normal([n_hidden_units,n_classes]))
}
biases={
# shape(128,)
'in':tf.Variable(tf.constant(0.1,shape=[n_hidden_units,])),
# shape(10,)
'out':tf.Variable(tf.constant(0.1,shape=[n_classes,]))
}
# 定义RNN主体结构
# RNN主体结构包括（input_layer,cell,output_layer）
def RNN(X, weights, biases):
# 原始数据X是三维数据，我们需要将它变换为2维数据才能使用weights的矩阵乘法
# Xshape==>（128batches*28steps,28inputs）
X=tf.reshape(X,[-1,n_inputs])
# X_in = W*X+b
X_in = tf.matmul(X,weights['in'])+biases['in']
# X_in==>(128batches,28steps,128hidden)换回三维
X_in=tf.reshape(X_in,[-1,n_steps,n_hidden_units])
# 创建cell
lstm_cell=tf.contrib.rnn.BasicLSTMCell(n_hidden_units,forget_bias=1.0,state_is_tuple=True)
init_state=lstm_cell.zero_state(batch_size,dtype=tf.float32)
outputs,final_state=tf.nn.dynamic_rnn(lstm_cell,X_in,initial_state=init_state,time_major=False)
# 输出到隐藏层
outputs=tf.unstack(tf.transpose(outputs,[1,0,2]))
results=tf.matmul(outputs[-1],weights['out'])+biases['out']
return results
pred=RNN(x,weights,biases)
cost=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y,logits=pred))
train_op=tf.train.AdamOptimizer(lr).minimize(cost)
# 训练RNN
correct_pred=tf.equal(tf.argmax(pred,1),tf.argmax(y,1))
accuracy=tf.reduce_mean(tf.cast(correct_pred,tf.float32))
init=tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
step=0
while step*batch_size