算法 4：支持向量机

欢迎来到机器学习的世界 
博客主页：卿云阁

欢迎关注点赞收藏⭐️留言

本文由卿云阁原创！

本阶段属于练气阶段，希望各位仙友顺利完成突破

首发时间：2021年5月7日

✉️希望可以和大家一起完成进阶之路！

作者水平很有限，如果发现错误，请留言轰炸哦！万分感谢！

---

目录

一、概述

二. 支持 向量机（核方法）

三，支持向量机解决分类问题

四、支持向量机解决回归问题

支持向量机 （ Support Vector Machine ， SVM ）是一种应用范围非常广泛的算法，既可以用于分类，也可以用于回归。 本节将介绍如何将线性支持向量机应用于二元分类问题。

目标：以间隔（margin ）最大化为基准，得到更好的决策边界。

一、概述

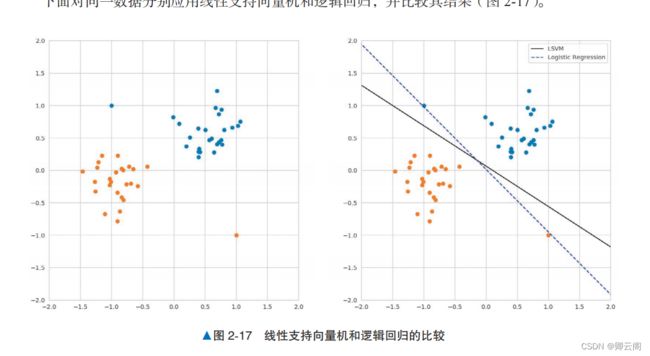
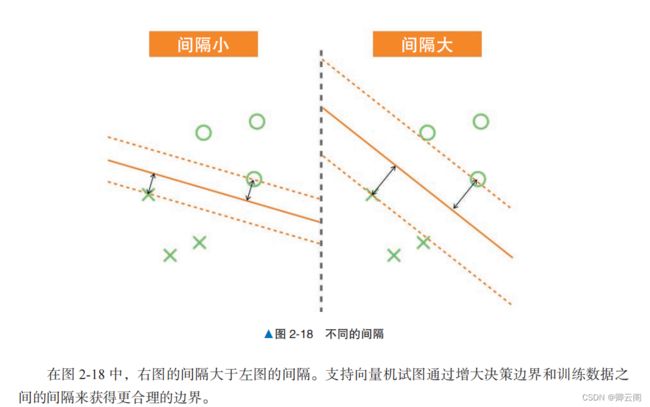
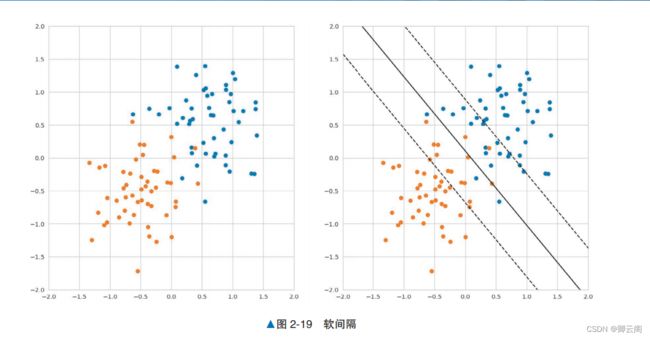
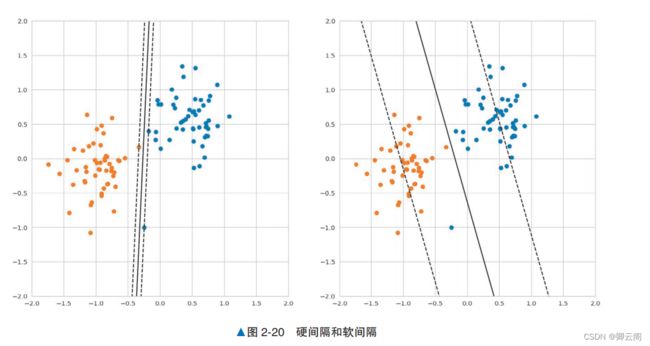
概述

下面对同一数据分别应用线性支持向量机和逻辑回归，并比较其结果。

左图是学习前的数据，右图是从数据中学习后的结果。

右图中用黑色直线标记 的是线性支持向量机的决策边界，用蓝色虚线标记的是逻辑回归的决策边界。

下面来看一下线性支持向量机是如何从数据中学习的。

算法说明

数据中最接近决边界的数据与决策边界之间的距离就称为间隔 。

示例代码

下面生成线性可分的数据，将其分割成训练数据和验证数据，使用训练数据训练线性支持向量 机，使用验证数据评估正确率。另外，由于使用了随机数，所以每次运行的结果可能有所不同。

from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 生成数据
centers = [(-1, -0.125), (0.5, 0.5)]
X, y = make_blobs(n_samples=50, n_features=2,
 centers=centers, cluster_std=0.3)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = LinearSVC()
model.fit(X_train, y_train) # 训练
y_pred = model.predict(X_test)
accuracy_score(y_pred, y_test) # 评估

1.0

详细说明

软间隔和支持向量

一般来说，数据并不是完全可以线性分离的，所以要允许一部分数据进入间隔内侧，这种情况叫作软间隔 。

基于线性支持向量机的学习结果，我们可以将训练数据分为以下 3 种。

1. 与决策边界之间的距离比间隔还要远的数据：间隔外侧的数据。

2. 与决策边界之间的距离和间隔相同的数据：间隔上的数据。

3. 与决策边界之间的距离比间隔近，或者误分类的数据：间隔内侧的数据。

其中，我们将间隔上的数据和间隔内侧的数据特殊对待，称为 支持向量 。支持向量是确定决策 边界的重要数据。间隔外侧的数据则不会影响决策边界的形状。 由于间隔内侧的数据包含被误分类的数据，所以乍看起来通过调整间隔，使间隔内侧不存在数

据的做法更好。 但对于线性可分的数据，如果强制训练数据不进入间隔内侧，可能会导致学习结果对数据过拟合。 使用由两个标签组成的训练数据训练线性支持向量机而得到的结果如图 2-20 所示。

左图是不允许数据进入间隔内侧的硬间隔的情况，右图是允许数据进入间隔内侧的

软间隔的情况。 另外，我们在蓝色点表示的训练数据中特意加上了偏离值。

比较两个结果可以发现，使用了硬间隔的图 2-20 中的左图上的决策边界受偏离值的影响很大； 而在引入软间隔的图 2-20 中的右图上的学习结果不容易受到偏离值的影响。

在使用软间隔时，允许间隔内侧进入多少数据由超参数决定。

---

 二. 支持 向量机（核方法）

引例：

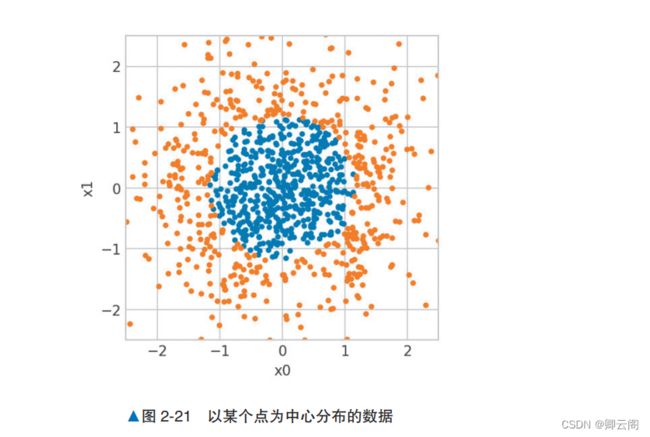
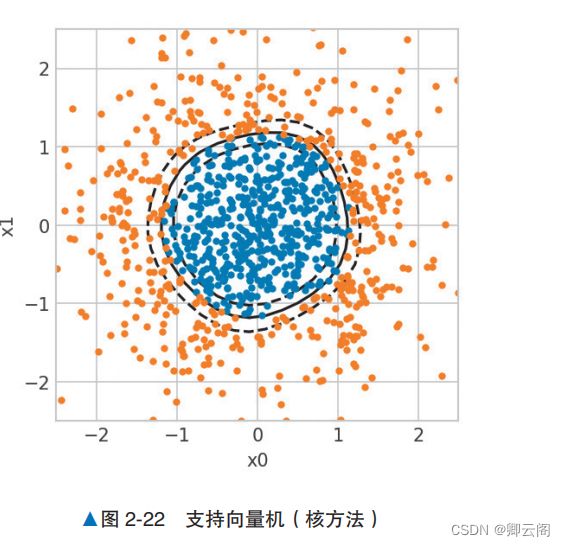
通过在支持向量机中引入 核方法 （ kernel methods ）这个技巧，那些无法人力标注特征值的复杂 数据也能被处理。当然，这个算法现在也用于解决各种分类和回归问题。

概述

线性支持向量机通过最大化间隔，可以得到尽可能远离数据的“好的”决策边界。但是由于决

策边界必定为直线，所以它很难对如图 2-21 所示的“每个标签的边界为曲线的数据”进行分类。

 为了分隔如图 2-21 所示的数据，模型需要学习曲线的线性决策边界。支持向量机可以使用核方法学习复杂的决策边界。例如，对这次的数据使用核方法，模型可以学到如图 2-22 所示的圆形 的决策边界。 

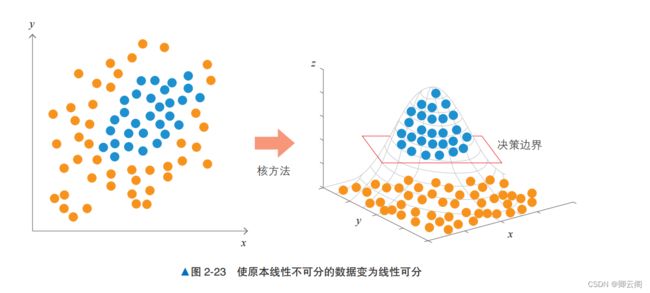
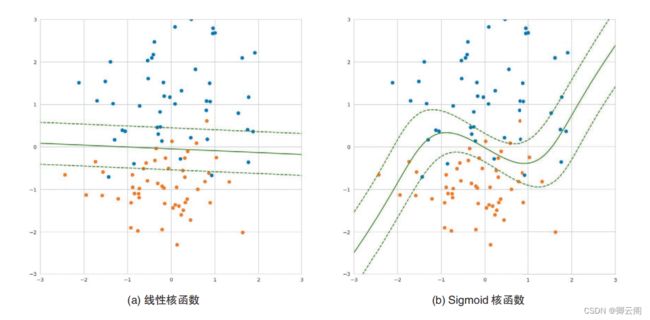
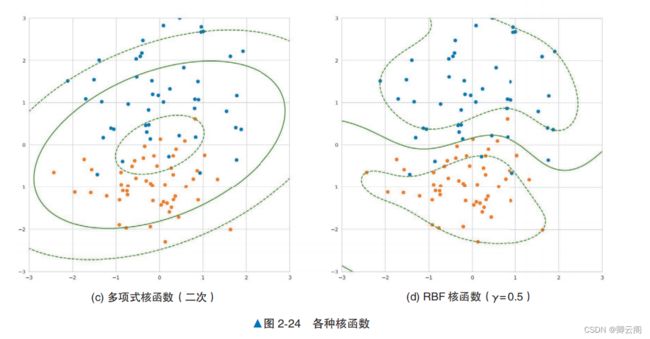
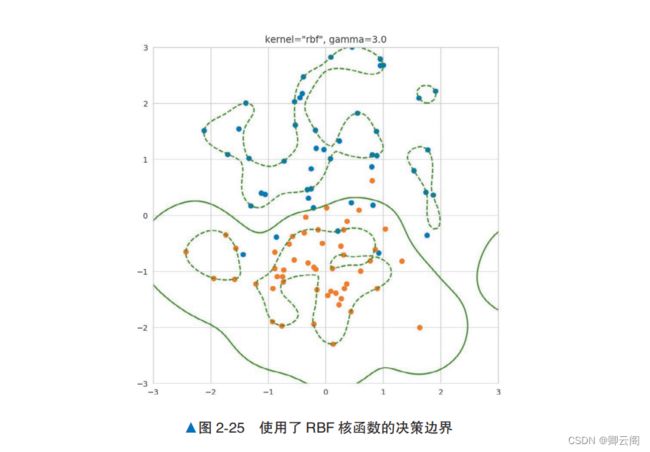
算法说明

核方法的一个常见解释是“将数据移动到另 一个特征空间，然后进行线性回归”。 对于这个

解释，我们再详细地看一下。 首先，思考一下如何使线性不可分数据成为 线性可分数据。假设有一个比训练数据更高维的 空间，训练数据中的每一个点都对应着这个高维

空间中的一个点。在这个高维空间中，训练数据 对应的点是可以线性分离的，实际的训练数据是 来自于该高维空间的投影。 一旦有了这样的空 间，模型就可以在高维空间中使用支持向量机来学习决策边界。最后，将高维空间的决策边界投影 到由原始特征形成的向量空间上，得到决策边界。 图 2-23 所示为在高维空间中对数据进行线性分离的情形，该数据原本是线性不可分的。

虽然构建线性分离的高维空间非常困难，但通过一个叫作 核函数 的函数，核方法就可以使用在 高维空间中学习到的决策边界，而无须构建具体的线性分离的高维空间。

“详细说明”部分将介绍具有代表性的核函数。

示例代码

下面通过示例代码来看一下使用核方法的支持向量机如何学习呈圆形分布的数据的决策边界。 我们生成呈圆形分布的数据，将其拆分为训练数据和验证数据，使用训练数据训练模型，使用验证 数据评估正确率。代码中没有明确指定使用哪个核方法，这是因为代码默认使用 RBF （ Radial Basis Function，径向基函数）核方法。

from sklearn.svm import SVC
from sklearn.datasets import make_gaussian_quantiles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 生成数据
X, y = make_gaussian_quantiles(n_features=2, n_classes=2, n_samples=300)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = SVC()
model.fit(X_train, y_train) 
y_pred = model.predict(X_test) 
accuracy_score(y_pred, y_test)

0.9666666666666667

详细说明

学习结果因核函数而异

核方法中可以使用的核函数多种多样。使用不同的核函数，得到的决策边界的形状也不同。图 2-24 所示为使用具有代表性的核函数在相同的数据上训练支持向量机的结果，这些核函数分别是线性核函数、Sigmoid 核函数、多项式核函数和 RBF 核函数。

图 2-24a 中的线性核函数等价于线性支持向量机。图 2-24b 中使用 Sigmoid 函数中可以看出，通过改变核函数，模型学习到了曲线的决策边界。另外，图 2-24c 中的多项式核函（二 次）学习到了圆形的决策边界。从图 2-24d 中可以看到 RBF 核函数是如何学习更复杂的决策边界的。

注意点

使用核方法后，我们就无法清楚地知道支持向量机使用的是什么特征了。在将 RBF 作为核函

数，并将 RBF 核函数的超参数 γ 设置为 3.0 时，模型学习的结果如图 2-25 所示。通过增加这个超参数的值，模型会从数据中学习更复杂的决策边界。

图 2-25 中的模型学习的是一个复杂的决策边界，但我们已经不知道模型使用的是什么特征了。 核方法适合用于“相比特征的可解释性更看重精度”的场景。还需要注意的是，得到的决策边界不 一定是通过示例代码学习到的那种一目了然的决策边界。 由于这些特点，在使用支持向量机时，不宜立即使用非线性核函数，在此之前，应先使用线性 核函数进行分析，以了解数据。

三，支持向量机解决分类问题

线性支持向量机分类：

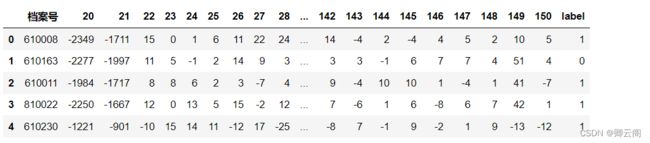
使用呼吸数据集

from sklearn.svm import LinearSVC
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
dataset = pd.read_excel('d:\\huqidata.xlsx')
data = dataset.iloc[:,1:-1]   #从1列到最后一列为呼气数据的特征数据
label = dataset.iloc[:,-1]    #最后一类为标签，1代表不吸烟，0代表吸烟
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(data,label,test_size=0.45,random_state=10)

model = LinearSVC()
model.fit(x_train, y_train) # 训练

y_pred = model.predict(x_test)
accuracy_score(y_pred, y_test) # 评估

非线性支持向量机分类

2.1 方式1：转换数据集添加多项式特征

要对数据集通过PolyolynomialFeaturenomialFeature进行转换，增加特征

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf = Pipeline((
    ("poly_features", PolynomialFeatures(degree=3)),
    ("scaler", StandardScaler()),
    ("svm_clf", LinearSVC(C=10, loss="hinge"))
))

polynomial_svm_clf.fit(X, y)

Pipeline(memory=None,
         steps=[('poly_features',
                 PolynomialFeatures(degree=3, include_bias=True,
                                    interaction_only=False, order='C')),
                ('scaler',
                 StandardScaler(copy=True, with_mean=True, with_std=True)),
                ('svm_clf',
                 LinearSVC(C=10, class_weight=None, dual=True,
                           fit_intercept=True, intercept_scaling=1,
                           loss='hinge', max_iter=1000, multi_class='ovr',
                           penalty='l2', random_state=None, tol=0.0001,
                           verbose=0))],
         verbose=False)

核函数

常用的核函数的适用情况：

线性核:主要用于线性可分的情况。我们可以看到特征空间到输入空间的维度是一样的，其参数少|速度快。对于线性可分数据，其分类效果很理想，因此我们通常首先尝试用线性核函数来做分类，看看效果如何，如果不行再换别的。
多项式核：多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。
高斯核：高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。
拉普拉斯核
Sigmoid核：采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。
实践中核函数的选取依据：
因此，在选用核函数的时候，如果我们对我们的数据有一定的先验知识，就利用先验来选择符合数据分布的核函数；如果不知道的话，通常使用交叉验证1的方法，来试用不同的核函数，误差最小的即为效果最好的核函数，或者也可以将多个核函数结合起来，形成混合核函数。在吴恩达的课上，也曾经给出过一系列的选择核函数的方法：

如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；
如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

多项式核
由于添加多项式特征在特征多时会产生大量的新特征，运行速度会变得很慢。
可以理解成，不用往数据集中添加大量新特征，却能够得到同样好的结果，的一种数学方法。

参数解释：

kernel：在算法中使用的内核类型。它必须是’linear’，‘poly’，‘rbf’，‘sigmoid’，'precomputed’或者callable之一

degree:多项式核函数的次数（‘poly’）。被所有其他内核忽略。同PolynomialFeatures类，指定的是多项式的阶数

coef0：核函数中的独立项。它只在’poly’和’sigmoid’中很重要。控制高阶多项式和低阶多项式对模型的影响

C：错误术语的惩罚参数C，默认为1

from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline((
 # 不用使用PolynomialFeatures给数据集添加新特征了
 ("scaler", StandardScaler()),
 ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
 ))
poly_kernel_svm_clf.fit(X, y)

 

Pipeline(memory=None,
         steps=[('scaler',
                 StandardScaler(copy=True, with_mean=True, with_std=True)),
                ('svm_clf',
                 SVC(C=5, cache_size=200, class_weight=None, coef0=1,
                     decision_function_shape='ovr', degree=3,
                     gamma='auto_deprecated', kernel='poly', max_iter=-1,
                     probability=False, random_state=None, shrinking=True,
                     tol=0.001, verbose=False))],
         verbose=False)

高斯核（rbf核）(默认项）

使用相似函数（高斯径向基函数），增加相似特征。
它适用于特征少，数据量正常的情况下，因此是SVC类该项参数的默认值

参数：
gamma：值越大，拟合程度越高
C：同样，值越大，拟合程度越高

rbf_kernel_svm_clf = Pipeline((
    ("scaler", StandardScaler()),
    ("svm_clf", SVC(kernel="rbf", gamma=5, C=0.01))
))

rbf_kernel_svm_clf.fit(X, y)

Pipeline(memory=None,
         steps=[('scaler',
                 StandardScaler(copy=True, with_mean=True, with_std=True)),
                ('svm_clf',
                 SVC(C=0.01, cache_size=200, class_weight=None, coef0=0.0,
                     decision_function_shape='ovr', degree=3, gamma=5,
                     kernel='rbf', max_iter=-1, probability=False,
                     random_state=None, shrinking=True, tol=0.001,
                     verbose=False))],
         verbose=False)

四、支持向量机解决回归问题

不同于SVM分类试图找到两个类别间尽可能大的“街道”，SVM回归试图让尽可能多的样本进入街道。

线性SVM回归

from sklearn.svm import LinearSVR
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
dataset = pd.read_excel('d:\\huqidata.xlsx')
data = dataset.iloc[:,1:-1]   #从1列到最后一列为呼气数据的特征数据
label = dataset.iloc[:,-1]    #最后一类为标签，1代表不吸烟，0代表吸烟
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(data,label,test_size=0.45,random_state=10)

svm_reg = LinearSVR(epsilon=0.5)
svm_reg.fit(x_train, y_train)


y_pred = model.predict(x_test)
accuracy_score(y_pred, y_test) # 评估

0.878968253968254

/usr/local/lib/python3.6/dist-packages/sklearn/svm/base.py:929: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  "the number of iterations.", ConvergenceWarning)





LinearSVR(C=1.0, dual=True, epsilon=0.5, fit_intercept=True,
          intercept_scaling=1.0, loss='epsilon_insensitive', max_iter=1000,
          random_state=None, tol=0.0001, verbose=0)

 非线性SVM回归

同非线性SVM分类，使用核函数

from sklearn.svm import  SVR
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
dataset = pd.read_excel('d:\\huqidata.xlsx')
data = dataset.iloc[:,1:-1]   #从1列到最后一列为呼气数据的特征数据
label = dataset.iloc[:,-1]    #最后一类为标签，1代表不吸烟，0代表吸烟
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(data,label,test_size=0.45,random_state=10)

svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(x_train, y_train)


y_pred = model.predict(x_test)
accuracy_score(y_pred, y_test) # 评估

0.878968253968254

/usr/local/lib/python3.6/dist-packages/sklearn/svm/base.py:193: FutureWarning: The default value of gamma will change from 'auto' to 'scale' in version 0.22 to account better for unscaled features. Set gamma explicitly to 'auto' or 'scale' to avoid this warning.
  "avoid this warning.", FutureWarning)





SVR(C=100, cache_size=200, coef0=0.0, degree=2, epsilon=0.1,
    gamma='auto_deprecated', kernel='poly', max_iter=-1, shrinking=True,
    tol=0.001, verbose=False)