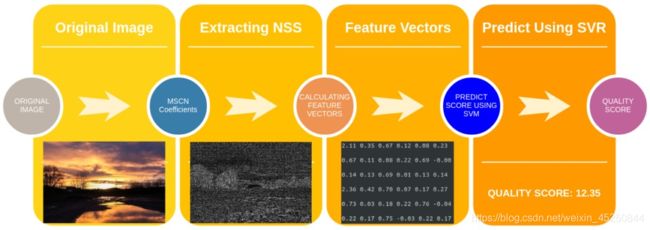
图像质量评估-BRISQUE
![]()
1. 介绍
1.1 什么是图像质量评估Image Quality Assessment (IQA)?
图像质量评价(IQA)算法以任意图像作为输入,输出质量分数作为输出。有三种类型的IQA:
- 全参考图像质量评价
适用情形:您有一个“干净”参考(非扭曲)图像,以衡量您的扭曲图像的质量。此度量可用于评估图像压缩算法的质量,在该算法中,我们可以访问原始图像及其压缩版本。 - 半参考图像质量评价
适用情形:如果没有参考图像,而是具有一些选择性信息的图像(例如,水印图像)来比较和测量失真图像的质量。 - 无参考图像质量评价
适用情形:算法得到的唯一输入是要测量其质量的图像
1.2 无参考图像质量评价
在这篇文章中,我们将讨论一个无参考图像质量评价的IQA度量算法,称为盲/无参考图像空间质量评估器Blind/Referenceless Image Spatial Quality Evaluator (BRISQUE)。在深入研究这个理论之前,让我们先了解两个基本术语:
- 失真图像(扭曲图像)
顾名思义,失真图像是指被模糊、噪声、水印、颜色变换、几何变换等因素扭曲的原始图像。下图是TID 2008数据库中使用的图像失真情况。
- 自然图像
自然图像是指由相机直接拍摄没有后期处理的图像。以下自然图像和失真图像的示例。左图是自然图像,右图是失真图像。
正如你所能想象的,图像清晰度与图像是失真的还是自然的没有关系。例如,当视频被巧妙地用运动模糊渲染时,由于故意模糊,算法可能会对其质量产生混淆。因此,我们必须在正确的背景下使用这种正确的图像质量评价方法来度量图像。
1.3 图像质量评估(IQA)数据集
图像质量好于坏是一个主观问题。为了获得一个优秀的图像质量评估算法,我们需要给出许多图像的算法示例和它们的质量分数。谁为这些训练图像给定质量得分?当然是人类。但我们不能仅仅依靠一个人的意见。因此,我们需要综合评估个人的意见,并为图像分配0(最佳)和100(最差)之间的平均分数。该分数在学术文献中称为平均质量分数。幸运的是我们不需要自己收集这些数据,有一个数据集称为TID 2008已经被用于研究目的。有关TID2008的信息见:
https://pdfs.semanticscholar.org/6dd3/7b57f3391b438fa588f98a1c2067365ae5ca.pdf
如下图所示,TID2008图像质量得分范围为0到100,得分越小,主观质量越好。

2. 盲/无参考图像空间质量评估器(BRISQUE)
- 提取自然场景统计(NSS)
- 计算特征向量
- 预测图像质量得分
2.1. 提取自然场景统计(NSS)
自然图像的像素强度的分布不同于失真图像的像素强度的分布。当归一化像素强度并计算这些归一化强度上的分布时,这种分布差异更加明显。特别是经过归一化后的自然图像像素强度服从高斯分布(Bell曲线),而非自然图像或畸变图像的像素强度不服从高斯分布。因此,通过像素高斯分布曲线是衡量图像失真的一种方法。我们已在下图中说明了这一点。

上图左图显示了一幅有添加人工效应的自然图像,符合高斯分布。右边为一个人造图像,但不适合同样的分布。
2.1.1 MSCN(Mean Subtracted Contrast Normalized)系数
有几种不同的方法来规范化图像。一种这样的归一化称为MSCN。下图显示了如何计算MSCN系数。

上图MSCN计算过程能够可视化为:

下面要讲述详细的数学推导,但不要让下面的数学吓倒你。数学之后的代码要简单得多,容易理解!

代码如下:
C++:
Mat im = imread("image_scenery.jpg"); // read image
cvtColor(im, im, COLOR_BGR2GRAY); // convert to grayscale
im.convertTo(im, 1.0/255); // normalize and copy the read image to orig_bw
Mat mu(im.size(), CV_64FC1, 1);
GaussianBlur(im, mu, Size(7, 7), 1.166); // apply gaussian blur
Mat mu_sq = mu.mul(mu);
// compute sigma
Mat sigma = im.size(), CV_64FC1, 1);
sigma = im.mul(im);
GaussianBlur(sigma, sigma, Size(7, 7), 1.166); // apply gaussian blur
subtract(sigma, mu_sq, sigma); // sigma = sigma - mu_sq
cv::pow(sigma, double(0.5), sigma); // sigma = sqrt(sigma)
add(sigma, Scalar(1.0/255), sigma); // to avoid DivideByZero Exception
Mat structdis(im.size(), CV_64FC1, 1);
subtract(im, mu, structdis); // structdis = im - mu
divide(structdis, sigma, structdis);
Python:
im = cv2.imread("image_scenery.jpg", 0) # read as gray scale
blurred = cv2.GaussianBlur(im, (7, 7), 1.166) # apply gaussian blur to the image
blurred_sq = blurred * blurred
sigma = cv2.GaussianBlur(im * im, (7, 7), 1.166)
sigma = (sigma - blurred_sq) ** 0.5
sigma = sigma + 1.0/255 # to make sure the denominator doesn't give DivideByZero Exception
structdis = (im - blurred)/sigma # final MSCN(i, j) image
2.1.2 相邻像素间的乘积关系
MSCN为像素强度提供了不错的归一化。然而自然退休与失真图像的差异不仅限于像素强度分布,还包括相邻像素之间的关系。为了捕获相邻像素的关系,在四个方向来求出相邻元素的两两乘积,即:水平(H),垂直(V),左对角线(D1),右对角线(D2)。
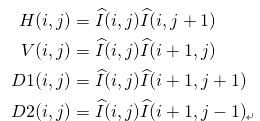
可以用Python和C++计算两两乘积,如下所示:
C++:
// declare shifting indices array
int shifts[4][2] = {{0, 1}, {1, 0}, {1, 1}, {-1, 1}};
// calculate pair-wise products for every combination of shifting indices
for(int itr_shift = 1; itr_shift <= 4; itr_shift++)
{
int* reqshift = shifts[itr_shift - 1]; // the required shift index
// declare shifted image
Mat shifted_structdis(imdist_scaled.size(), CV_64F, 1);
// BwImage is a helper class to create a copy of the image and create helper functions to access it's pixel values
BwImage OrigArr(structdis);
BwImage ShiftArr(shifted_structdis);
// calculate pair-wise component for the given orientation
for(int i = 0; i < structdis.rows; i++)
{
for(int j = 0; j < structdis.cols; j++) { if(i + reqshift[0] >= 0 && i + reqshift[0] < structdis.rows && j + reqshift[1] >= 0 && j + reqshift[1] < structdis.cols)
{
ShiftArr[i][j] = OrigArr[i + reqshift[0]][j + reqshift[1]];
}f
else
{
ShiftArr[i][j] = 0;
}
}
}
Mat shifted_new_structdis;
shifted_new_structdis = ShiftArr.equate(shifted_new_structdis);
// find the pairwise product
multiply(structdis, shifted_new_structdis, shifted_new_structdis);
}
Python:
# indices to calculate pair-wise products (H, V, D1, D2)
shifts = [[0,1], [1,0], [1,1], [-1,1]]
# calculate pairwise components in each orientation
for itr_shift in range(1, len(shifts) + 1):
OrigArr = structdis
reqshift = shifts[itr_shift-1] # shifting index
for i in range(structdis.shape[0]):
for j in range(structdis.shape[1]):
if(i + reqshift[0] >= 0 and i + reqshift[0] < structdis.shape[0] \ and j + reqshift[1] >= 0 and j + reqshift[1] < structdis.shape[1]):
ShiftArr[i, j] = OrigArr[i + reqshift[0], j + reqshift[1]]
else:
ShiftArr[i, j] = 0
可以使用cv2.warpAffine方法将两个for循环简化为几行代码。这将大大加快计算速度。
# create affine matrix (to shift the image)
M = np.float32([[1, 0, reqshift[1]], [0, 1, reqshift[0]]])
ShiftArr = cv2.warpAffine(OrigArr, M, (structdis.shape[1], structdis.shape[0])
2.2 计算特征向量
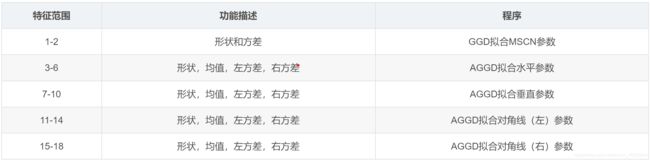
到目前为止,我们已经从原始图像派生了5个图像参数,即1个MSCN图像和4个两两乘积图像,以捕获相邻关系(水平、垂直、左对角、右对角)。接下来,我们将使用以上5个参数来计算尺寸为36×1的特征向量。请注意,原始输入图像可以是任何尺寸(宽度/高度),但特征向量的大小始终为36×1。
通过将MSCN图像拟合到广义高斯分布(GGD)来计算36×1特征向量的前两个元素。GGD有两个参数-一个用于形状,另一个用于方差。
接下来,用非对称广义高斯分布(AGGD)拟合相邻元素乘积参数中的任何一个。AGGD是广义高斯拟合(GGD)的不对称形式。它有四个参数,即形状,均值,左方差和右方差。由于有4个两两相乘图像参数,我们最终得到16个值。
因此,我们最终得到了特征向量的18个元素。图像缩小到原来大小的一半,并重复相同的过程以获得18个新的数字,使总数达到36个。下表概述了这一点。
2.3 图像质量评分的预测
在典型的机器学习应用程序中,首先将图像转换为特征向量。然后将训练数据集中所有图像的特征向量和输出(在这种情况下是质量分数)输入到支持向量机(SVM)等学习算法中。可以下载tid2008数据并且训练一个支持向量机来解决这个问题,但是在这篇文章中,我们将简单地使用作者提供的经过训练的模型。
下载地址:http://www.ponomarenko.info/tid2008.htm
首先加载训练后的模型,然后利用模型产生的支持向量预测概率,利用LIBSVM预测最终的质量分数。需要注意的是,特征向量首先被缩放为-1到1,然后用于预测。我们共享Python和C++实现这一点的方法:
3. 结果和代码
3.1 结果
我们对四种类型的失真进行了度量。以下是理论上每个失真的最终质量分数。但是这个仅仅是理论上的,实际上效果在不同电脑和不同图像分辨率上并不是这样的。对于图像压缩结果可能大相径庭。不过总的来说BRISQUE效果不错,但是精度不够,主要是svm还需要自己训练。
3.2 代码
TODO
4. 最后
![]()