LSTM 单变量多步预测航空乘客复杂版
前言
- LSTM 航空乘客预测单步预测的两种情况。 简单运用LSTM 模型进行预测分析。
- 加入注意力机制的LSTM 对航空乘客预测采用了目前市面上比较流行的注意力机制,将两者进行结合预测。
- 多层 LSTM 对航空乘客预测 简单运用多层的LSTM 模型进行预测分析。
- 双向LSTM 对航空乘客预测双向LSTM网络对其进行预测。
- MLP多层感知器 对航空乘客预测简化版 使用MLP 对航空乘客预测
- CNN + LSTM 航空乘客预测采用的CNN + LSTM网络对其进行预测。
- ConvLSTM 航空乘客预测采用ConvLSTM 航空乘客预测
- LSTM的输入格式和输出个数说明 中对单步和多步的输入输出格式进行了解释
- LSTM 单变量多步预测航空乘客
本文采用LSTM网络多步进行预测,复杂版
程序
复杂版
前一步预测下两步
# 单变量,多步预测
# 第二种方法尝试
from pandas import DataFrame
from pandas import Series
from pandas import concat
from pandas import read_csv
from pandas import datetime
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from math import sqrt
from matplotlib import pyplot
from numpy import array
# 将时间序列转换为监督类型的数据序列
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = DataFrame(data)
cols, names = list(), list()
# 这个for循环是用来输入列标题的 var1(t-1),var1(t),var1(t+1),var1(t+2)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j + 1, i)) for j in range(n_vars)]
# 转换为监督型数据的预测序列 每四个一组,对应 var1(t-1),var1(t),var1(t+1),var1(t+2)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j + 1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j + 1, i)) for j in range(n_vars)]
# 拼接数据
agg = concat(cols, axis=1)
agg.columns = names
# 把null值转换为0
if dropnan:
agg.dropna(inplace=True)
print(agg)
return agg
# 对传入的数列做差分操作,相邻两值相减 ,消除趋势的标准方法是差分化数据
def difference(dataset, interval=1):
diff = list()
for i in range(interval, len(dataset)):
value = dataset[i] - dataset[i - interval]
diff.append(value)
return Series(diff)
# 将序列转换为用于监督学习的训练和测试集
def prepare_data(series, n_test, n_lag, n_seq):
# 提取原始值
raw_values = series.values
# 将数据转换为静态的
diff_series = difference(raw_values, 1)
diff_values = diff_series.values
diff_values = diff_values.reshape(len(diff_values), 1)
# 重新调整数据为(-1,1)之间
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_values = scaler.fit_transform(diff_values)
scaled_values = scaled_values.reshape(len(scaled_values), 1)
# 转化为有监督的数据X,y
supervised = series_to_supervised(scaled_values, n_lag, n_seq)
supervised_values = supervised.values
# 分割为测试数据和训练数据
train, test = supervised_values[0:-n_test], supervised_values[-n_test:]
return scaler, train, test
# 匹配LSTM网络训练数据
def fit_lstm(train, n_lag, n_seq, n_batch, nb_epoch, n_neurons):
# 重塑训练数据格式 [samples, timesteps, features]
X, y = train[:, 0:n_lag], train[:, n_lag:]
X = X.reshape(X.shape[0], 1, X.shape[1])
# 配置一个LSTM神经网络,添加网络参数
model = Sequential()
model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))
model.add(Dense(y.shape[1]))
model.compile(loss='mean_squared_error', optimizer='adam')
# 调用网络,迭代数据对神经网络进行训练,最后输出训练好的网络模型
for i in range(nb_epoch):
model.fit(X, y, epochs=nb_epoch, batch_size=n_batch, verbose=0, shuffle=False)
model.reset_states()
return model
# 用LSTM做预测
def forecast_lstm(model, X, n_batch):
# 重构输入参数 [samples, timesteps, features]
X = X.reshape(1, 1, len(X))
# 开始预测
forecast = model.predict(X, batch_size=n_batch)
# 结果转换成数组
return [x for x in forecast[0, :]]
# 利用训练好的网络模型,对测试数据进行预测
def make_forecasts(model, n_batch, train, test, n_lag, n_seq):
forecasts = list()
# 预测方式是用一个X值预测出后三步的Y值
for i in range(len(test)):
X, y = test[i, 0:n_lag], test[i, n_lag:]
# 调用训练好的模型预测未来数据
forecast = forecast_lstm(model, X, n_batch)
# 将预测的数据保存
forecasts.append(forecast)
return forecasts
# 对预测后的缩放值(-1,1)进行逆变换
def inverse_difference(last_ob, forecast):
# invert first forecast
inverted = list()
inverted.append(forecast[0] + last_ob)
# propagate difference forecast using inverted first value
for i in range(1, len(forecast)):
inverted.append(forecast[i] + inverted[i - 1])
return inverted
# 对预测完成的数据进行逆变换
def inverse_transform(series, forecasts, scaler, n_test):
inverted = list()
for i in range(len(forecasts)):
# create array from forecast
forecast = array(forecasts[i])
forecast = forecast.reshape(1, len(forecast))
# 将预测后的数据缩放逆转换
inv_scale = scaler.inverse_transform(forecast)
inv_scale = inv_scale[0, :]
# invert differencing
index = len(series) - n_test + i - 1
last_ob = series.values[index]
# 将预测后的数据差值逆转换
inv_diff = inverse_difference(last_ob, inv_scale)
# 保存数据
inverted.append(inv_diff)
return inverted
# 评估每个预测时间步的RMSE
def evaluate_forecasts(test, forecasts, n_lag, n_seq):
for i in range(n_seq):
actual = [row[i] for row in test]
predicted = [forecast[i] for forecast in forecasts]
rmse = sqrt(mean_squared_error(actual, predicted))
print('t+%d RMSE: %f' % ((i + 1), rmse))
mae = mean_absolute_error(actual, predicted)
print('t+%d MAE: %f' % ((i + 1), mae))
# 在原始数据集的上下文中绘制预测图
def plot_forecasts(series, forecasts, n_test):
# plot the entire dataset in blue
pyplot.plot(series.values)
# plot the forecasts in red
for i in range(len(forecasts)):
off_s = len(series) - n_test + i - 1
off_e = off_s + len(forecasts[i]) + 1
xaxis = [x for x in range(off_s, off_e)]
yaxis = [series.values[off_s]] + forecasts[i]
pyplot.plot(xaxis, yaxis, color='red')
# show the plot
pyplot.show()
# 加载数据
series = read_csv('airline-passengers.csv', usecols=[1], engine='python')
#series = series.values.astype('float64')
# print(len(series))
# 配置网络信息
n_lag = 1 # 时间步长
n_seq = 2 # 预测步长
n_test = len(series)-int(len(series)*0.8) # 测试集长度
# print(n_test)
# LSTM 中的超参数
n_epochs = 10
n_batch = 1
n_neurons = 32
# 准备数据
scaler, train, test = prepare_data(series, n_test, n_lag, n_seq)
# 准备预测模型
model = fit_lstm(train, n_lag, n_seq, n_batch, n_epochs, n_neurons)
# 开始预测
forecasts = make_forecasts(model, n_batch, train, test, n_lag, n_seq)
# 逆转换训练数据和预测数据
forecasts = inverse_transform(series, forecasts, scaler, n_test + 2)
# 逆转换测试数据
actual = [row[n_lag:] for row in test]
actual = inverse_transform(series, actual, scaler, n_test + 2)
# 比较预测数据和测试数据,计算两者之间的损失值
evaluate_forecasts(actual, forecasts, n_lag, n_seq)
# 画图
plot_forecasts(series, forecasts, n_test + 2)
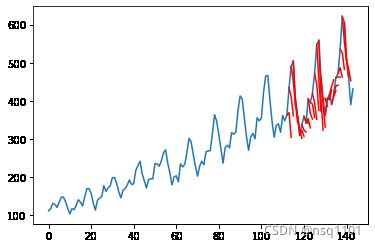
结果展示:
t+1 RMSE: 49.609525
t+1 MAE: 41.189362
t+2 RMSE: 83.477126
t+2 MAE: 68.233978
总结
复杂版的,代码写成函数形式,作为一个整体,可复用性强,理解起来稍微麻烦一些。
总体的思路,代码还是一样,处理数据的时候有点变化。