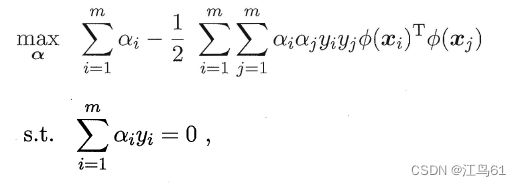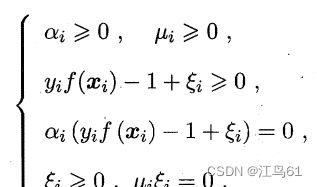《机器学习》（西瓜书）第六章

6.1 间隔与支持向量

对于两类训练样本分开的超平面很多，我们需要找到对训练样本局部扰动的“容忍”性最好的那一个。对未见示例的泛化能力最强。（鲁棒性：一个系统或组织抵御或克服不利条件的能力。）距离超平面最近的几个训练样本能够正确分类，他们被称为“支持向量”，两个异类支持向量到超平面的距离之和称为“间隔”。为什么需要通过放缩w和b使得距离超平面最近的样本点所对应的值恰好为+1与-1？

间隔：

为了找到具有“最大间隔”的超平面，需要使参数最小，这就是支持向量机（SVM）的基本模型。

即转化为：(6.6)

6.2 对偶问题

拉格朗日乘子法：

寻找多元函数在一组约束下的极值的方法。可将有d个变量与k个约束条件的最优化问题，转化为具有d+k个变量的无约束优化问题。

对(6.6)的每条约束加拉格朗日乘子，可以写出拉格朗日函数。

（6.8）

对上式求w和b的偏导

代回

 

就可以得到（6.6）的对偶问题。

其中对偶问题是拉格朗日乘子，又原式有不等式约束，故上述过程要满足KKT(Karush-Kuhn-Tucker)条件，即：

KKT条件是非线性规划最优解的必要条件，关于KKT详见Karush-Kuhn-Tucker (KKT)条件 - 知乎

因此，我们不难知道，在训练结束后，大部分训练样本不需要保留，支持向量是最重要的。

SMO算法

先固定αi之外的所有参数，然后求αi上的极值。由于存在约束∑αiyi = 0，所以固定αi以外的其他变量，αi可由其他变量导出。于是，SMO每次选择两个变量αi和αj，这样，在参数初始化后，SMO不断执行以下步骤：

• 选取一对需要更新的变量αi和αj；
• 固定αi和αj以外的参数，求解以得更新后的αi和αj。

6.3 核函数

 对于异或问题或者非线性映射问题，我们将样本从原始空间映射到一个更高维的特征空间，使其在这个空间内线性可分。如果原始空间使有限维，那么一定存在一个高维特征空间使其样本可分。

令表示x映射后的特征向量。

仍然有，

由6.2可知其对偶函数

求解上式涉及到计算φ(xi)Tφ(xj)，这是样本xi与xj映射到特征空间之后的内积，直接计算很困难，故设计一个函数：

我们这里引入的函数即为“核函数”，进行核函数展开，这一展开式又称为“支持向量模式”。

定理6.1（核函数），只要一个对称函数所对应的核矩阵半正定，它就能作为核函数。核函数如果选择不佳，就意味着样本映射到了一个不合适的特征空间，很可能导致性能不佳。

6.4 软间隔与正则化

在现实中往往很难确定合适的核函数使得训练样本在特征空间中线性可分。即使恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。

为了缓解这个问题，我们在此允许SVM在一些样本上出错，引入“软间隔”。但是，必须要求在最大化间隔的同时，不满足约束的样本应尽可能少，于是优化目标写为：

C>0，为一常数，l0/1是“0/1损失函数”，

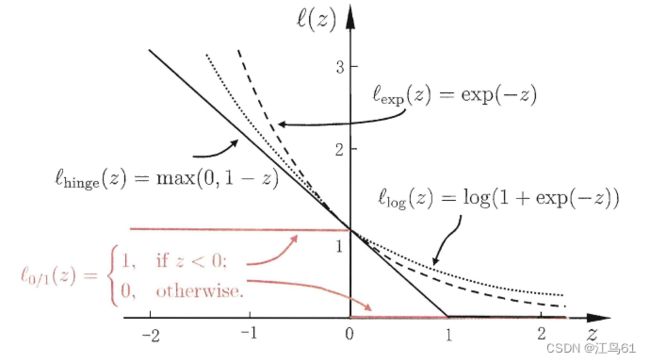
 因为l0/1非凸、非连续，所以会寻找一些函数来代替，被称为“替代损失”，

 分别为：hinge损失，指数损失，对率损失。与硬间隔的对偶问题的差别在于：对偶变量αi的约束不同。

正则化：

机器学习中经常会在损失函数中加入正则项，称之为正则化（Regularize）。

目的：防止模型过拟合

原理：在损失函数上加上某些规则（限制），缩小解空间，从而减少求出过拟合解的可能性

 6.5 支持向量回归

支持向量回归(Support Vector Regression, SVR)假设我们能容忍f(x)与y之间最多有ε的偏差。

6.6 核方法

 上式表示定理对损失函数没有性质，并且对正则化项Ω仅要求单调递增，甚至不要求其是凸函数，意味着对一般的损失函数和正则化项，优化问题的最优解都可表示为核函数的线性组合。