基于深度强化学习的机器人运动控制研究进展 | 无模型强化学习 | 元学习
1.基于深度强化学习的机器人运动控制研究进展
1.1 深度强化学习
1.1.1 强化学习简介:
强化学习(Reinforcement Learning, RL)利用试错机制与环境进行交互,旨在通过最大化累积延迟奖励(Return)的方式来学习到最优策略。强化学习本质上是通过参数化的函数逼近 “状态-动作”的映射关系,以求解MDP的最优策略。
1.1.2 为什么要将深度学习引入强化学习?
强化学习受自身结构与学习能力的约束,多以解决低维问题为主,在处理高维连续状态-动作空间下的控制问题时,难以有效求解,且无法通过人工设定对高维数据进行合适的特征表达.因此,通过引入神经网络对特征进行有效表示,将高维连续的状态与动作进行 离散降维,以达到降低任务复杂度、提高学习速度的效果,使得强化学习拓展至高维空间成为可能。
1.1.3 DRL原理
1.智能体与环境交互时刻进行,并通过DL方法感知和观察高维度目标,得到当前环境下具体的状态信息;
2.基于预期回报来评价各动作的价值函数(以此激励智 能体),并通过RL方法得到某种适应性策略,将当前状态映射为相应的动作;
3.环境对该动作做出相应反馈,智能体以此进行下一时刻的观察.通过以上过程的不断循环,智能体最终可以得到完成既定任务的最优行动策略.
1.2 DRL方法
1.2.1 基于值函数
基于值函数的深度强化学习是用DNN逼近奖励值函数,以激励机器人等智能体获得最优行动策略,主要包括DQN及其改进方法.
(1)DQN
DQN训练过程中使用相邻的4帧游戏画面作为网络的输入,经过多个卷积层和全连接层,输出当前状态下可选动作的Q值,采用带有参数θ的卷积神经网络作为函数逼近器,并且定期从经验回放池中采样历史数据,利用随机梯度下降算法(Stochastic GradientDescent, SGD)更新网络参数,实现端到端的学习控制。
DQN 包含两个结构相同的 Q 网络.一个用于与环境进行交互,选择动作,并优化模型参数,被称为主 Q 网络;另一个用于计算目标Q 值,优化主 Q 网络,被称为目标 Q 网络.为了减小目标Q 值和当前Q 值的相关性,主 Q 网络每隔若干时间步将 网 络 参 数 传 递 给 目 标 Q 网 络 一 次,即 延 时 更 新.DQN 的另一个 主 要 特 点 是 使 用 了 经 验 回 放 (experiencereGplay).其将与环境交互得到的状态转移情况和对应得到
的奖励作为经验数据存入经验回放池,用于计算目标 Q 值.由于目标Q 值与通过主 Q 网络计算的Q 值之间存在误差,因此使用均方误差梯度下降,并通过反向传播来更新主 Q 网络参数,从而求解 RL问题.
(2)DDQN
DQN始终是选取下一状态中最大Q值所对应的动作,而在选择与评价动作过程 中,其都是基于目标Q网络的参数,导致在学习过程中会出现过高估计Q值的问题.
与DQN选择和评价动作均基于同一个参数θ不同的是,DDQN将动作选择和策略评估分开,解决了DQN训练过程中过高估计动作值函数的问题。
对DQN算法进行改进: 在深度双Q网络中训练2个Q网络,采用在线Q网络参数θ来估计策略并以此进行将来动作的选择,而目标Q网络参数θ−用来估 计Q值以衡量动作价值,最终通过网络之间交替更新达到了解耦的效果.
(3)Dueling DQN
在大多基于视觉感知 的DRL任务中,状态与所对应动作之间的值函数不尽相同.尤其是在某些特定状态下,值函数的大小与动作无关,便会出现价值与动作分离的问题。
Dueling DQN保 留原有DQN的卷积层以及全卷积层,并结合优势学(Advantage Learning)的思想,将卷积层提取到的抽 象特征分流到全连接层的两条支路中,分别代表状态值函数V(s)和某个状态下的动作优势函数A(s, a),其中,动作优势函数A(s, a)指在状态s下,某动作a相对于平均状态动作对而言的优势,用于衡量当前状态下各个动作的相对优劣程度.最后,输出模块通过聚合操 作将两条支路组合起来以得到各个动作的奖励值函数Q(s, a).
(4)NAF
离散控制的DQN算法难以应对真实环境中大量存在的高维连续控制问题.
归一化优势函数(Normalized Advantage Functions, NAF)算法,以扩展DQN算法在连续控制问题中的应用.NAF是基于值函数的DRL算法在连续 控制问题上的首次尝试,但其设定过多约束和假设条 件,目前并未提出一种在普遍意义上解决值函数与连续动作空间相容性的方法
1.2.2 基于值函数
基于策略梯度的深度强化学习利用DNN逼近策略并利用策略梯度方法求得最优策略,其用于机器人控制的主要典型算法包括TRPO、PPO、DDPG以及A3C.
(1)TRPO
置信域策略优化算法(Trust Region Policy Optimization, TRPO)
TRPO首先使用单路径采样(Single-path Sampling)或蜿蜒采样(Vine Sampling)得到一系列状态动作对,通过蒙特卡洛方法估计得到Q函数值; 然后利用所得Q值对样本求平均得到优化问题中目标和约束的估计; 最后,采用共轭梯度和线搜索方法近似解决约束优化问题并以此更新参数,实现对机器人运动任务的最优控制.但当策略选用深层神经网络表示时,会使问题求解面临十分庞大的计算量,这也是TRPO算法目前所存在的主要缺陷.
(2)PPO
为降低TRPO的计算复杂度,Schulman等[14]在其与行动者-评论家(Actor-Critic, AC)框架结合的基础之上提出了近端策略优化算法(Proximal Policy Optimization, PPO).
PPO算法减少了TRPO中采用共轭梯度和线搜索方法近似求解的过程,提升了算法的训练速度和可实施性.
同时,为了使新旧策略更新相 对接近,PPO算法中采用了两种解决方法: 1) 在目标 函数中添加了剪切(Clip)项; 2) 引入惩罚(Penalty)项,通过自动调整惩罚系 数来限制KL散度值的大小,以减小新旧策略中动作 概率分布之间的差异性,从而代替TRPO中约束对于 策略更新幅度的限制.
(3) DDPG
与TRPO算法中随机性策略输出的动作概率不 同,确定性策略输出的是动作,无法进行环境探索,而 通过环境交互进行学习是强化学习的必要过程,一时 间如何将确定性策略方法应用于强化学习中成为一 个难以解决的问题.
基于AC框 架 的 确 定 性 策 略 梯 度 算 法(Deterministic Policy Gradient, DPG),利用离线策略(Off-policy) 即不使用 相同策略进行动作选择和评估,使得确定性策略可 支持智能体进行环境探索行为,其中评估策略使用确定性策略,动作策略使用随机策略.在DPG算法的基础上提出深度确定性策略梯 度算法(Deep Deterministic Policy Gradient, DDPG),利 用DNN逼近价值函数和确定性策略,使得其在连续 任务上的应用得以扩展,可以看作DQN与AC框架的 结合,其算法结构如图5所示
DDPG包括4个神经网络,由主体网络与目标网 络两部分组成,分别通过策略梯度和损失函数更新 网络参数值以获得最优控制策略,针对使用DNN逼 近值函数而普遍存在的不稳定问题,其借鉴DQN的 思路,在DPG算法中使用经验回放与目标网络,以减 少数据间的相关性,并采取AC框架结构,用Critic最 大化Q值,而Actor再利用Critic对动作的梯度进行学 习,使得DDPG适用于解决机械臂运动等连续控制问 题,具有较高的样本利用效率.
(4)A3C
针对值函数逼近过程中的不稳定性,除了经 验 回 放 机 制 以 外,通 过 异 步 数 据 采 集 同 样 也 可 以解决.2016年,Mnih等[18]基于AC框架提出了异步优势动作评价算法(Asynchronous Advantage ActorCritic, A3C),使 用 异 步 梯 度 下 降 法 优 化DNN控 制 器
A3C通过子网络复制来收集 样本计算的累积梯度,使得多个智能体实现并行训 练,且子网络的更新参数与主网络共享
1.2.3 总结
1.3 仿真平台
首先通过在仿真 环境下训练学习以获取运动技能或控制策略(控制 器),再将其引入真实环境,利用原始传感信息,进行技 能回放(或策略控制),使得机器人在复杂未知环境下 做出最优的自主行动决策.相比于直接让实体机器人 在真实环境中进行反复试错学习的不现实性,仿真训 练为基于DRL的机器人运动控制方法提供了一种低 成本、高效率、可观测的学习途径.
2.无模型强化学习研究综述
2.1 引言
在实际应用中,根据agent是否通过与环境交互获得的 数据来预定义环境动态模型,将 RL 分为模型化强化学习和无模型强化学习
(1)模型化强化学习指先在与环境交互的数据中创建环境动 态模型,然后基于该模型学习最优策略.它一般包含状态转
移预测和奖励预测两个独立模型但当面对的问题具有复杂的状态动作空间时,准确估计环境动态模型存在巨大挑战.
面对复杂的应用场景时,模型化强化学习若存在模型误差,性能会远低于无模型强化学习。
(2)无模型强化学习指agent与环境进行实时交互和探索, 并直接对得到的经验数据进行学习,最终实现累积收益最大
化或达到特定目标。
然而,无模型强化学习通常需要大量的训练样本和 训练时间,因此如何提高数据利用率和学习效率是无模型强 化学习的研究重点。
2.2 马尔可夫决策过程
RL指agent通过不断试错来积累经验,探索优化状态到 动作之间的映射,最终得到最优策略,同时最大化累积收益的过程.
马 尔 可 夫 决 策 过 程 (Markov Decision Process, MDP)是序贯决策问题的经典表达形式,是通过交互学习实现最终目标的理论框架.
MDP一般被描述为五元组(S,A,P,R,γ),其中 S 代表有限状态集,A 代表有限动作集,P代表状态转移概率,R代表奖励函 数,γ代表用于计算整个过程累积收益的折扣因子。
马尔可夫决策过程定义:
假设状态转换具有马 尔可夫性,即转换到当前状态的概率仅与上一状态和上一动 作有关.环境从状态s通过动作a 转移至s′的概率和期望 奖励可表示为:
在 RL中,agent的目标为最大化累积收益的期望值,价值函数利用收益期望值评估当前状态或给定状态与动作下的agent表现.
vπ(s)为策略π下状态s的状态价值函数.对于 MDP,vπ(s)可表示为:
Gt表示从当前状态开始到终止状态结束这个过程中所 有收益按一定比例衰减的总和.因此,vπ(s)又可表示为:
vπ的贝尔曼方程
同理,qπ(s,a)代表策略π下,状态s采取动作a的动作价值函数. 对于MDP,qπ(s,a)可表示为:
qπ的贝尔曼方程
为解决 RL 问题,可通过寻找较优的价值函数来得到较 优策略,通常最优价值函数定义为所有策略下对应价值函数 中的最大者,对应的策略即为最优策略,即:
v∗ 代表最优状态价值函数,q∗ 代表最优动作价值函数.
为了得出最优策略π∗ ,RL引入了贝尔曼最优方程其阐述了最优策略对应的最优价值函数下, 各状态的价值一定等于此状态下最优动作的收益期望.
2.3 无模型强化学习的方法
主要有基于价值和基于策略两类
2.3.1 基于价值的方法
(1)时序差分法
时序差分法(TemporalGDifference,TD)结合了动态规划 和蒙特卡洛算法的优点,其不需要环境动态模型,也不需要完整的状态序列,而是根据贝尔曼方程得到的收益期望值近似 表示收益.因此,TD 只需要两个连续状态和对应的即时收 益即可求解 RL问题.
TD分为在线策略(on policy)和离线策略(off policy)两 类学习算法,最常见的在线策略是 SARSA 算法,最常见的离 线策略是 Q Learning算法
SARSA 算法,其中S代表状态 (State),A代表动作(Action),R 代表奖励(Reward).在迭代过程中,agent首先基于ε贪婪法在当前状态s选择一个动作a,执行动作后环境向前推进一个时间步长并转移到下 一个状态s′,同时agent获得一个即时奖励R.在新的状态 s′,agent基于ε贪婪法选择一个动作a′,但并不执行,只用于更新价值函数q(s,a)
Q Learning算法与SARSA 的不同之处在于,agent基于状态s′使用贪婪法选择动作,即直接选择 Q 值最大的动作来更新价值函数q(s,a)
两者的区别主要在于:在线策略 一般只有一个策略进行价值迭代,即ε婪法;而离线策略一般有两个策略,ε贪婪法用于选择动作,贪婪法用于更新价值函数.
SARSA 与 Q Learning算法的拓扑图
自己找的资料解释Q learning与SARSA
Q-Learning的目的是学习特定State下、特定Action的价值。是建立一个Q-Table,以State为行、Action为列,通过每个动作带来的奖赏更新Q-Table。
Q-Learning是off-policy的。异策略是指行动策略和评估策略不是一个策略。Q-Learning中行动策略是ε-greedy策略,要更新Q表的策略是贪婪策略。
Sarsa全称是state-action-reward-state’-action’。 也是采用Q-table的方式存储动作值函数;而且决策部分和Q-Learning是一样的, 也是采用ε-greedy策略。不同的地方在于 Sarsa 的更新方式是不一样的。
1.Sarsa是on-policy的更新方式,它的行动策略和评估策略都是ε-greedy策略。
2.Sarsa是先做出动作后更新。
Q-Learning算法,先假设下一步选取最大奖赏的动作,更新值函数。然后再通过ε-greedy策略选择动作。
Sarsa算法,先通过ε-greedy策略执行动作,然后根据所执行的动作,更新值函数。
(2) 深度 Q Learning算法
当 RL 问题中状态维度较高或动作空间规模较大时,可 采用近似表示价值函数的方法进行建模.
最常见的价值函数近似表示方法为深度神经网络,因此 研究人员基于 QGLearning算法,结合深度神经网络提出了深 度 QGLearning算法(DeepQGLearningNetwork,DQN)
2.3.2 基于价值的方法
基于价值函数的 RL方法在连续动作空间方面处理问题 的能力不足,且无法解决随机策略问题,因此研究人员相继提 出了诸多基于策略函数的 RL 方法,其采用与价值函数近似表示相同的思路对策略函数进行拟合,此时策略π被描述为 包含参数θ的策略函数:
策略梯度通过端到端的方式不断计算当前策略下的 agent累积收益与策略参数的梯度,最终梯度收敛得到最优策略.
在策略梯度方法中,只要π(a|s,θ)对参数可导,策略就可通过任意方式参数化.一般常用的策略参数化方法是 SoftMax和高斯策略.
2.3.3 基于价值策略结合的方法
(1)行动者评论家算法
基于价值函数和策略函数相结合的方法称为行动者评论家算 法 (Actor Critic).Actor Critic包括 Actor和 Critic
两部分,其中 Actor基于策略函数,负责与环境交互进而选择 动作;Critic基于价值函数,负责评估 Actor并指导其下一状态动作.
(2)异步的优势行动者评论家算法
异步的优势行动者评论家算法 (Asynchronous Advantage Actor critic,A3C)利用多线程异步执行与环境进行交互.
3.元学习研究综述
深度学习和强化学习严重受限于小样本数据集,容易发生过拟合,无法实现类似于人类强泛化性的学习能力。元学习为此应运而生,以累积经验的方式形成“价值观”,基于本身的认知和价值判断能力对模型进行调整或优化,让智能体在实际环境中能快速学会各项复杂新任务,实现真正意义上的人工智能。
3.1 元学习基本原理
元学习随着对每一项历史任务的学习和经验积累,在学习新任务时可以变得更加容易,所需要的训练样本更少,同时还能保证一定的算法精度.元学习旨在学会如何学习,区别于以映射方式为主的深度学习和以试错方式为主的强化学习.
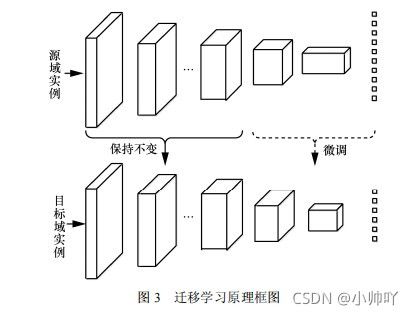
迁移学习与元学习都希望通过利用先前学到的知识快速地掌握新的技能或概念。但是,迁移学习侧重于在实例空间进行训练,通过
优化单个整体任务作为转移源来训练基础模型。常用的已训练好的开源网络模型有 VGG 、 ResNet 及GoogleNet等。选择合适的模型直接迁移到目标网络上,再利用少量标注样本对目标网络进行微调;
而元学习是在任务空间中进行训练。每当模型尝试学习某项任务时,无论成功与否,模型都会获得有用的经验,整合这些经验形成智能体的“价值观”,代表一种会学习的能力,即抽象成函数 F(x)。若出现新的任务,在“价值观”的协助下,模型继续学习新任务的极少量样本,即可快速适应和掌握新任务,也就是抽象出一个个对应新任务 i 的函数fi(x)。元学习比迁移学习对未知新任务的适应有着更好的稳健性。
3.2 元学习方法
1.基于权重的元学习方法
基于权重的元学习方法最大的一个成果就是让网络自身学会初始化有效的权重,可以克服迁移学习难以应付小样本的问题,不再需要手动配置模型的初始化权重参数,通过学习历史任务的经验,估计得到各新任务对应的初始化参数组,以保证模型能快速适应新任务,借助少量的新任务样本进行训练即能获得最佳性能。
2.基于优化器的元学习方法
这类方法不用人为配置 Adam等优化器,将新任务上的优化器设计工作交由元学习器完成。即元学习器根据以往任务的学习经验捕获单个梯度坐标的训练动态或为新任务量身定做一个高效的优化器,以让模型在拥有更为合适的优化器的情况下实现快速学习新任务。
3.基于损失函数的元学习方法
与基于优化器的元学习方法类似,以通过历史任务来学习如何预测损失函数的方式建模。
设计一个可微的损失函数,通过优化其策略以最大程度地减少这种损失,获得较高的回报。基于强化学习中奖励函数的设计思想,泛化至损失函数,即通过学到的策略网络编码为学到的损失函数。
4.基于度量的元学习方法
其关键是要学习到一个嵌入网络,使原始输入可以转换为合适的表示,并实现样本实例与待测实例之间相似度比较。
5.基于注意力机制的元学习方法
训练出一个模型使其能在面对新任务时把“注意力”都放在关键点上,即直接关注最为核心的部分。Ren 等[27]设计了一个基于元学习的注意力吸引网络(attention attractor network,AAN),先是经过监督学习以训练一个起初原有类别的分类器,若出现新增类别,于训练和测试节点中联合元学习正则器以训练得到新类别分类器,再结合起初原有类别与新增类别并用于优化刚才提到的元学习正则器,让它在新旧类别结合后仍然保持作用。Hou 等[28]提出一个交叉注意力网络(cross attention network),给所有输入的图像对分别生成注意力图,以突出目标物体所在的区域,使模型可以把“注意力”都集中在这部分区域,提取出更好的特征,以快速适应未知类别的问题。基于注意力机制的元学习方法有着较好的泛化性能和可解释性能。
6.基于超参数的元学习方法
以元学习的方式不断地优化调整学习率、正则化强度等超参数直至适合新任务。
7.基于网络结构的元学习方法
利用强化学习机制去训练一个循环神经网络(recurrent neural network,RNN),让其学会自动生成神经网络的元学习方法。先是利用循环神经网络在搜索空间上推算估计得到一个网络架构,再对这估计生成的网络架构进行训练和验证,以验证的准确率作为奖励反馈到循环神经网络中,循环神经网络根据奖励继续优化生成另外一个网络架构进行训练和验证,重复这样的过程直至循环神经网络获得最佳性能,学会如何生成好的网络架构。
8.基于黑盒模型的元学习方法
习方法有着较好的泛化性能和可解释性能。
6.基于超参数的元学习方法
以元学习的方式不断地优化调整学习率、正则化强度等超参数直至适合新任务。
7.基于网络结构的元学习方法
利用强化学习机制去训练一个循环神经网络(recurrent neural network,RNN),让其学会自动生成神经网络的元学习方法。先是利用循环神经网络在搜索空间上推算估计得到一个网络架构,再对这估计生成的网络架构进行训练和验证,以验证的准确率作为奖励反馈到循环神经网络中,循环神经网络根据奖励继续优化生成另外一个网络架构进行训练和验证,重复这样的过程直至循环神经网络获得最佳性能,学会如何生成好的网络架构。
8.基于黑盒模型的元学习方法
基于黑盒模型的元学习方法分为基于内部记忆单元与基于外部存储两类。









![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MOO68KHs-1636021056381)(D:\截图\截图未命名9.jpg)]](http://img.e-com-net.com/image/info8/406f750ea5714a95be6b36e24617cb77.jpg)
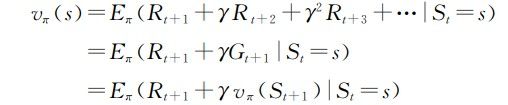
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XZdEphvl-1636021056382)(D:\截图\截图未命名12.jpg)]](http://img.e-com-net.com/image/info8/1486d49f67e142d2ad44c02bb78baffc.jpg)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mlPxtnsX-1636021056383)(D:\截图\截图未命名13.jpg)]](http://img.e-com-net.com/image/info8/55007712d0a442a690fbf93f41bc7ba2.jpg)
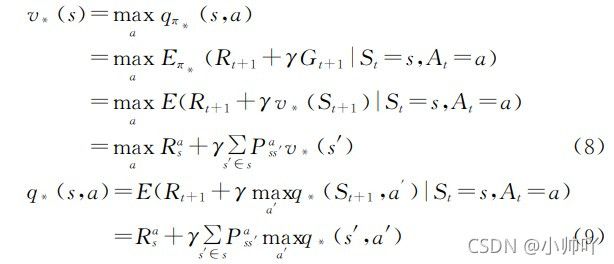



![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OUNG3D7j-1636021056387)(D:\截图\截图未命名21.jpg)]](http://img.e-com-net.com/image/info8/b2b2fe8642ea49c390173105a8a078d0.jpg)