Community Detection Based on Fish School Effect

摘要：受现实生活中鱼类鱼群效应的启发，本文将网络设想为一个生态系统，并提出了一种新的动态模型，旨在以更直观的方式揭示群落。基于该新模型，我们设计了一种基于鱼群效应（CDFSE）的社区检测算法。

优点：首先，它可以实现高质量的社区划分。其次，它不需要设置参数。第三，它没有主张对网络结构的先验知识；更重要的是，它具有时间复杂度低的特点，并且在大规模网络中能够有效地识别社区结构

基本思想

在海洋网络中，有多种鱼类，这是初始状态；同一种类型的鱼相互吸引是因为它们的共同特征（它们都很相似），形成一个初始群体。集团本身和少量的鱼组将吸引和收集其他同类的鱼，因为他们更大的吸引力，形成一个大规模的集团，更有吸引力，更稳定，甚至吸引其他组形成一个更大的组。随着时间的推移，不同种类的鱼会根据其不同的特征被吸引到不同的群体中，即鱼群的稳定状态。

基于鱼群效应的群落检测检验过程

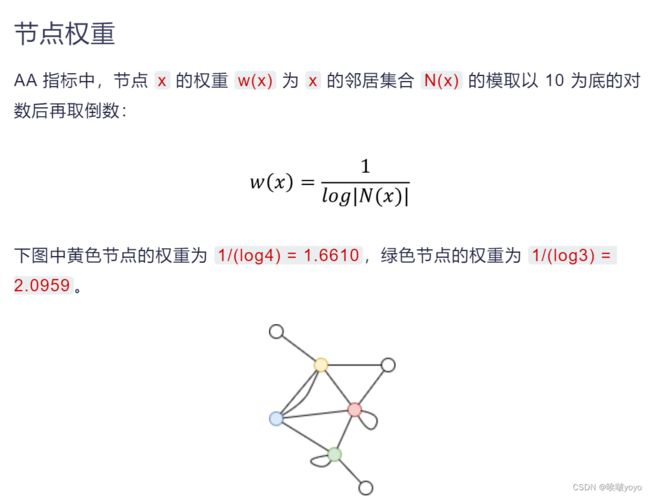
第一阶段：每条鱼都有自己的特征和共性，而且它们都是分散的。个体间的相似性是通过亚当-adar指数[26]（AA）的表达式来计算的 

AA 指标（Adamic-Adar Index）是一种基于网络结构信息定义的节点相似性指标。AA 指标用两个节点的共同邻居节点的权重和作为这两个节点的相似度

（ 例如，个体2和个体3之间的相似度为0.53，个体4和个体6之间的相似度为0.32，如图2 (a).所示）

 第二阶段，具有较大特征的鱼因为它们更大的相似性而相互吸引形成亚群。                              （例如，个体2和3、个体4和6、个体8、9和10、个体11和15比其他个体的相似性更大，因此它们分别是形成A、B、C和D亚群的前四个，如图2 (b).所示）

第三阶段，由于鱼群效应，吸引了越来越多的鱼类加入亚种群，形成大量的种群。                   （例如，个体1和个体2之间的亲和力为0.21，个体1和个体3之间的相似度为0.39，个体1和个体7之间的相似度为0.22。因此，与B组相比，A组对个体1更有吸引力。）

最后，个体1被A组吸引，鱼个体7、5和12被B组吸引，鱼个体13和14被d组吸引。从这个观点来看，每个个体都被不同的群体或社区所吸引

CDFSE算法优点

新颖、高效、简单、可扩展性

相关定义

定义1：（AA相似度指数）[26]给定无向网络G =（V，E），将节点v1和v2的AA相似度指数定义为CNv1v2是v1和v2的共同邻居节点

---

由于个体之间的吸引力不仅与相似性有关，而且与个体自身的程度有关，因此个体之间的吸引力被定义为个体的程度与个体之间的相似性的乘法。

 定义2：（个体吸引力）给定无向网络G =（V，E），节点v1对节点v2的吸引力定义为

SAAv1v2表示节点v1和v2之间的AA相似系数，Dv1表示节点v1的度。

---

定义3：（集群吸引力）给定无向网络G =（V，E），社区c对节点v的吸引力定义为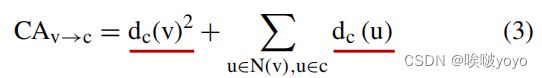 

 其中，dc (v)表示社区c中节点v的内部度。根据节点v到不同社区的边数，社区吸引力CAv→可以分为两种情况：一种是dc (v)不等式，另一种是dc (v)相等式。

  (1)当两个社区中的一个节点的内部度不相等时。例如，对于图3 (a)中的节点12，社区A的内部度为dA（12）= 1，而社区B的内部度为dB（12）= 2，社区A的节点12的内部度明显低于社区 B. 节点12对社区B的吸引力可能大于社区B A. 为了进一步确定这个吸引力，我们考虑了间接邻居对节点12的影响。在小区A中，节点3与节点1 2连接，节点3的度为5，dA (3) = 4，因此根据公式(3)可以将小区A对节点1 2的吸引力计算为CA1 2→A=1 2+4=5。在社区B中，节点7和8与节点12连接，节点7的程度为4，因此dB (7) = 3，节点8的度为4，dB (8) = 3，因此社区B对节点12的吸引力可以计算为CA12→B=2 2+3+3=10。由于群落B对节点12的吸引力强于群落A对节点12的吸引力，因此节点12更有可能加入群落B，如图3 (a)所示

(2)当一个节点的内部度在两个社区里相等时。例如，对于图3 (b)中的节点12，dA（12）=dB（12）=2，很难判断哪个社区A或B对节点12更有吸引力。因此，必须注意考虑在节点12中出现的间接邻居的影响。在社区A中，节点5和6与节点12连接，节点5的程度为5，因此dA (5) = 4，节点6的程度为5，dA (6) = 4，因此根据公式(3)，社区A对节点12的吸引力可以计算为CA12→A=2 2+4+4=12。在社区B中，节点9和10与节点12连接，节点9的度为3，因此dB (9) = 2，节点10的度为4，dB（10）= 3，因此根据公式(3)，可以计算出社区B对节点12的吸引力为CA12→B=2 2+2+3=9。因为社区A对节点12更有吸引力，所以节点12更有可能加入社区A，如图3 (b).所示

鱼群效应模型

该模型由网络初始化、亚种群形成和鱼群效应三个阶段组成

1)网络初始化

最初，每个个体都有自己的特征，并被视为一个独立的群体或个体，如图4的第一阶段所示。

2)亚群的形成

在第二阶段，资源较少的节点被剩余节点吸引，如图4所示，当Dv> max（Dv1）、v1∈N (v)时，节点v仍然属于原子群Cv。否则，节点v加入一个新的子组Cv1，其中Cv是节点v所属的社区，Dv表示节点v的度。

3）鱼群效应

在网络拓扑结构的驱动下，所有的节点都将能够在处理多次迭代后改变它们的吸引力。节点加入了不同的组，当节点所属的组的参数不再发生任何变化时，网络结构达到平衡状态。

CDFSE算法

1)网络初始化

最初，我们将每个节点描述为一个独立的个体或组。为了区分不同的节点，我们用一个数字来标记每个个体或组，以进行初始化。

2)核心组计算

在计算核心组之前，我们需要首先计算出个体的吸引力。个人的吸引力与资源和相似性有关。在网络结构中，我们应用节点的度来表示节点所拥有的资源，并使用AA相似度系数来表示节点之间的相似度。根据公式(2)，我们可以度量个体之间的吸引力。正是由于个体吸引的存在，网络中的节点相互吸引，形成一个子群（核心群）。我们可以通过一轮迭代来计算核心组。

3)鱼群效应模拟

根据本文提出的鱼群效应模型，亚种群之间的相互作用不断吸引其他个体加入，从而形成更大的亚种群。由于亚种群趋于稳定，可以模拟鱼群效应的过程。在社区中，我们使用标准化的互信息指数来评估每个社区分区的性能。随着时间的推移和拓扑结构的影响，网络结构达到了一个稳定的状态；从而可以得到最佳的划分。

结论

        受自然界鱼类网络的启发，本文提出了一种基于鱼群效应的社区检测模型，并根据该模型提出了一种社区检测算法CDFSE。CDFSE背后的中心思想是将网络看作一个动态系统，并研究其随时间的动态。网络中的个体会因为其共性和特征而形成子群体，而子群体会因为自己的吸引力而吸引其他个体形成大群体。随着时间的推移，所有的个体最终都会被吸引到不同的群体中，形成一个稳定的社区结构。实验结果表明，CDFSE算法在不同网络上表现较好，且性能优于其他比较算法。主要性能如下：首先，该算法比上述其他算法具有更高的效率和更好的社区检测质量；其次，该算法不需要设置参数，更简单、方便；第三，算法的时间复杂度小，可以应用于大规模网络；其次，该算法源自自然，符合自然规律，更接近真实网络，可以更好地应用于社区检测。本文的局限性在于，在实际数据集上与经典方法相比，只增加了时间复杂度来验证其有效性，而空间复杂度是进一步探索需要考虑的。