【 group convolution (分组卷积)详解】

卷积神经网络在图像处理中的地位已然毋庸置疑。卷积运算具备强大的特征提取能力、相比全连接又消耗更少的参数，应用在图像这样的二维结构数据中有着先天优势。然而受限于目前移动端设备硬件条件，显著降低神经网络的运算量依旧是网络结构优化的目标之一。本文所述的Separable Convolution就是降低卷积运算参数量的一种典型方法。

常规卷积运算

假设输入层为一个大小为64×64像素、三通道彩色图片。经过一个包含4个Filter的卷积层，最终输出4个Feature Map，且尺寸与输入层相同。整个过程可以用下图来概括。

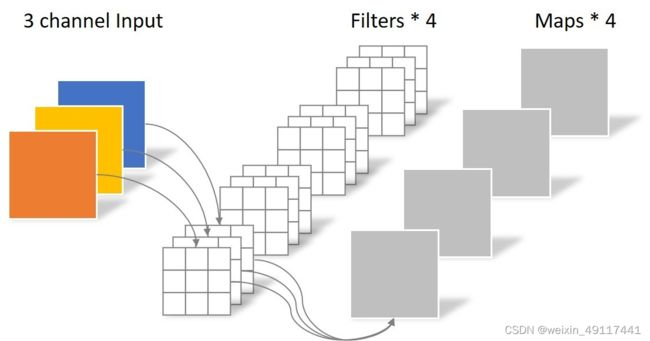
此时，卷积层共4个Filter，每个Filter包含了3个Kernel，每个Kernel的大小为3×3。因此卷积层的参数数量可以用如下公式来计算：

N_std = 4 × 3 × 3 × 3 = 108
Separable Convolution
Separable Convolution在Google的Xception[1]以及MobileNet[2]论文中均有描述。它的核心思想是将一个完整的卷积运算分解为两步进行，分别为Depthwise Convolution与Pointwise Convolution。

Depthwise Convolution

同样是上述例子，一个大小为64×64像素、三通道彩色图片首先经过第一次卷积运算，不同之处在于此次的卷积完全是在二维平面内进行，且Filter的数量与上一层的Depth相同。所以一个三通道的图像经过运算后生成了3个Feature map，如下图所示。

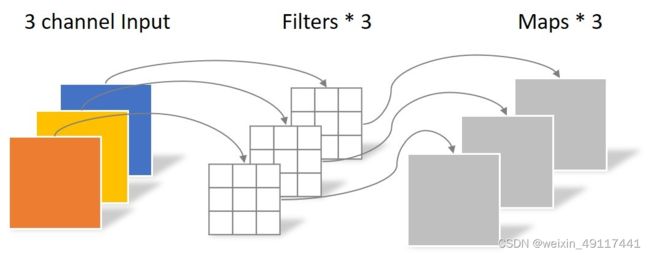
其中一个Filter只包含一个大小为3×3的Kernel，卷积部分的参数个数计算如下：

N_depthwise = 3 × 3 × 3 = 27

Depthwise Convolution完成后的Feature map数量与输入层的depth相同，但是这种运算对输入层的每个channel独立进行卷积运算后就结束了，没有有效的利用不同map在相同空间位置上的信息。因此需要增加另外一步操作来将这些map进行组合生成新的Feature map，即接下来的Pointwise Convolution。

Pointwise Convolution

Pointwise Convolution的运算与常规卷积运算非常相似，不同之处在于卷积核的尺寸为 1×1×M，M为上一层的depth。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个Filter就有几个Feature map。如下图所示。

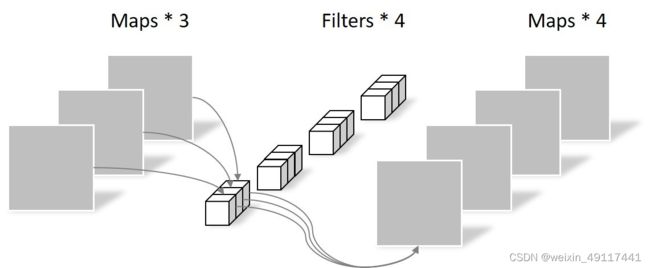
由于采用的是1×1卷积的方式，此步中卷积涉及到的参数个数可以计算为：

N_pointwise = 1 × 1 × 3 × 4 = 12

经过Pointwise Convolution之后，同样输出了4张Feature map，与常规卷积的输出维度相同。

参数对比

回顾一下，常规卷积的参数个数为：

N_std = 4 × 3 × 3 × 3 = 108

Separable Convolution的参数由两部分相加得到：

N_depthwise = 3 × 3 × 3 = 27
N_pointwise = 1 × 1 × 3 × 4 = 12
N_separable = N_depthwise + N_pointwise = 39

相同的输入，同样是得到4张Feature map，Separable Convolution的参数个数是常规卷积的约1/3。因此，在参数量相同的前提下，采用Separable Convolution的神经网络层数可以做的更深。

group convolution (分组卷积)详解

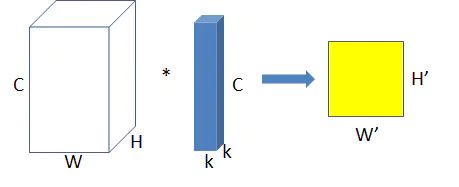
1.普通卷积：

上图为普通卷积示意图，为方便理解，图中只有一个卷积核，此时输入输出数据为：

• 输入feature map尺寸： W×H×C ，分别对应feature map的宽，高，通道数；
• 单个卷积核尺寸： k×k×C ，分别对应单个卷积核的宽，高，通道数；
• 输出feature map尺寸 ：W’×H’ ，输出通道数等于卷积核数量，输出的宽和高与卷积步长有关，这里不关心这两个值。
• 参数量 params=k^2C
  *运算量FLOPs=k^2CW’H’，这里只考虑浮点乘数量，不考虑浮点加。

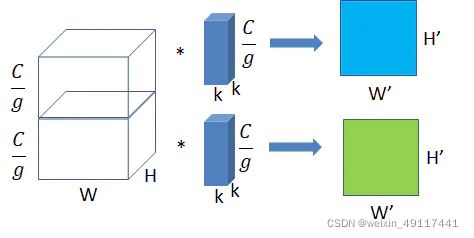
2.group convolution (分组卷积)

图2 分组卷积

将图一卷积的输入feature map分成组，每个卷积核也相应地分成组，在对应的组内做卷积，如上图2所示，图中分组数，即上面的一组feature map只和上面的一组卷积核做卷积，下面的一组feature map只和下面的一组卷积核做卷积。每组卷积都生成一个feature map，共生成个feature map。

• 输入每组feature map尺寸：W×H×C/g，共有g组；
• 单个卷积核每组的尺寸：k×k×C/g，一个卷积核被分成了g组；
• 输出feature map尺寸：W’×H’×g，共生成g个feature map。

现在我们再来计算一下分组卷积时的参数量和运算量：

• 参数量 params=k x k x C /g x g =k x k x C
• 运算量FLOPs=k x k x (C / g)×W’×H’×g=k x k x C x W’ x H’

我们居然用了同等的参数量运算量生成了g个feature map！！！
所以group conv常用在轻量型高效网络中，因为它用少量的参数量和运算量就能生成大量的feature map，大量的feature map意味着能够编码更多的信息！

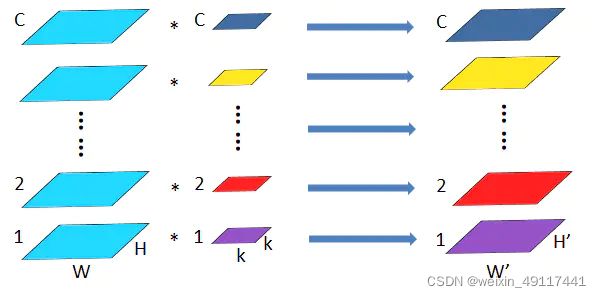
从分组卷积的角度来看，分组数g就像一个控制旋钮，最小值是1，此时g=1的卷积就是普通卷积；最大值是输入feature map的通道数C，此时g=C的卷积就是depthwise sepereable convolution，即深度分离卷积，又叫逐通道卷积。

3.深度分离卷积：

如上图所示，深度分离卷积是分组卷积的一种特殊形式，其分组数，其中是feature map的通道数。即把每个feature map分为一组，分别在组内做卷积，每组内的单个卷积核尺寸为，组内一个卷积核生成一个feature map。这种卷积形式是最高效的卷积形式，相比普通卷积，用同等的参数量和运算量就能够生成个feature map，而普通卷积只能生成一个feature map。
所以深度分离卷积几乎是构造轻量高效模型的必用结构，如Xception, MobileNet, MobileNet V2, ShuffleNet, ShuffleNet V2, CondenseNet等轻量型网络结构中的必用结构。