台湾大学李宏毅:图解卷积神经网络CNN
公众号:尤而小屋
作者:Peter
编辑:Peter
大家好,我是Peter~
本文记录的是台湾大学李宏毅老师对CNN卷积神经网络的讲解,图解非常易懂。涉及到的知识点:
- 卷积神经网络如何运用到图片分类问题
- 感受野 Receptive Field
- 步长Stride
- 填充Padding
- 参数共享share parameter
- 最大池化MaxPooling
- CNN全过程
仅个人理解学习
引言
CNN卷积神经网络最初主要是用于计算机视觉和图像处理中,比如图像分类:
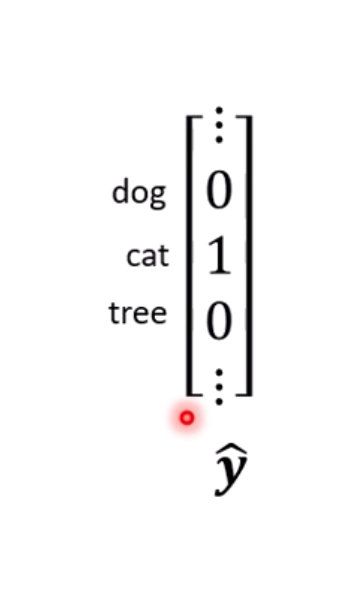
最终的分类数绝对维度:
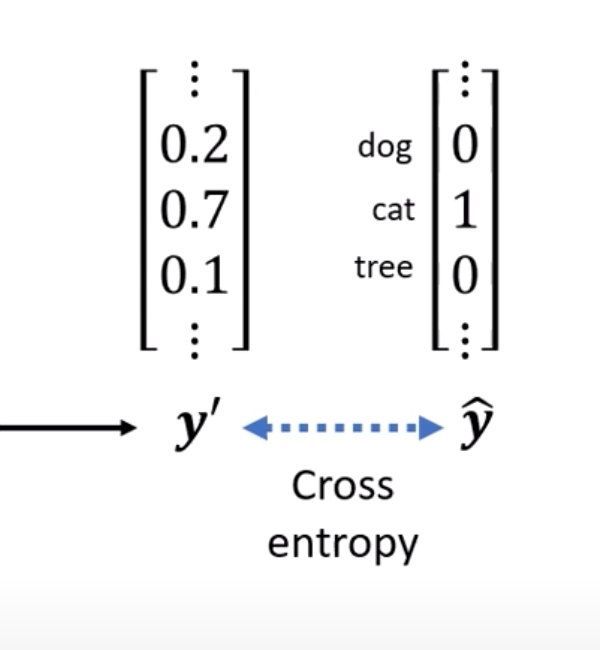
在模型中交叉熵的使用:最终通过概率分布求得每个类的概率值,最大值所在类作为最终的输出。
图片组成
图片一般是有RGB组成的,通常是3维:(height, width,channels)。
在喂入卷积神经网络之前需要将3维的向量拉直,变成一维向量(flatten操作):
拉直之后喂入全连接层:
问题1:如果隐藏层有1000个神经元,每个样本的输入是100*100*3,仅仅单层的总weights数是 3 ∗ 1 0 7 3*10^7 3∗107。参数增加的时候,模型表达能力更强,但是也增加了模型过拟合overfitting的风险。
在实际处理中,每个神经元(Neuron)不必和输入input的每个维度都有一个权重weight,也就是说部分维度可忽略。
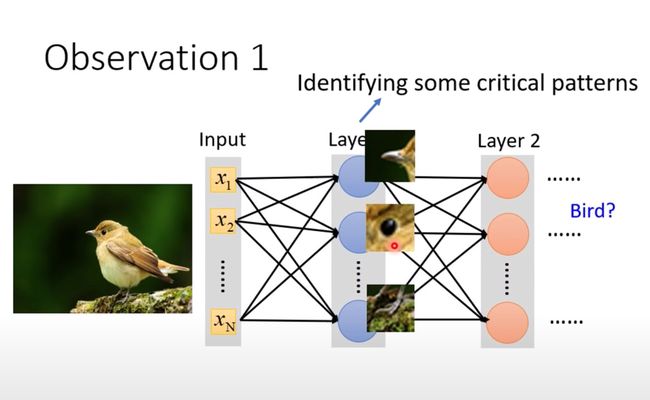
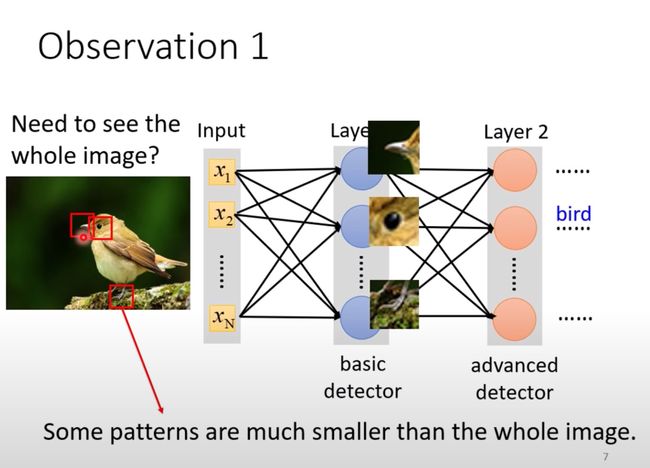
图像识别:找准突出点Pattern
在一张图片中我们识别出几个特殊点(Pattern)就能够对这个进行判断,将它归属于某个类,而不需要扫描整张图片。
案例中识别鸟嘴、鸟爪、鸟眼睛。一般人类也是抓住物件的重要来进行判断
CNN概念-感受野
什么是感受野
卷积神经网络CNN中存在一个概念:感受野Receptive Field。
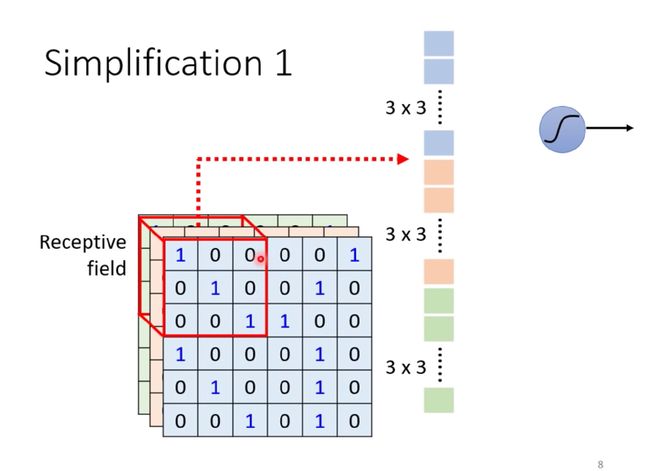
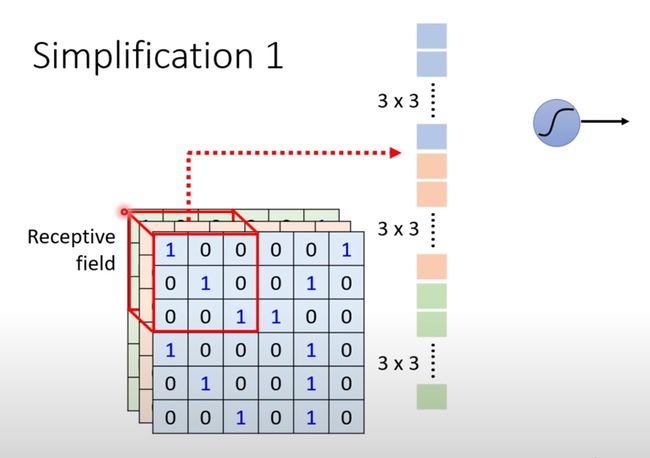
感受野:用来表示网络内部的不同位置的神经元对原始图像的感受范围的大小。
上图解释:上面右边的一个神经元关注自己的范围(左边红色框)
感受野作用
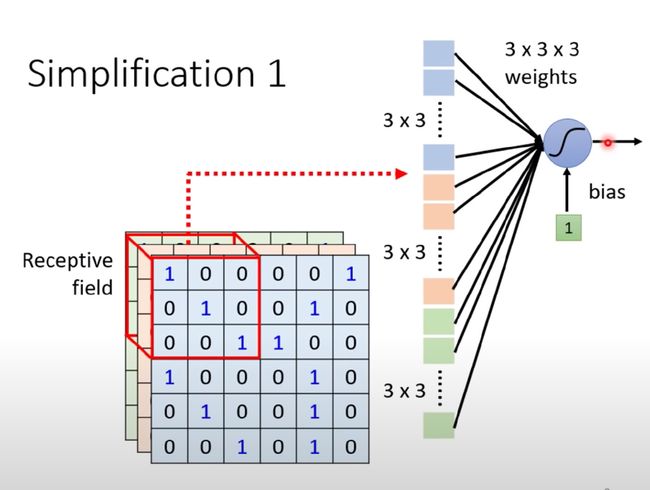
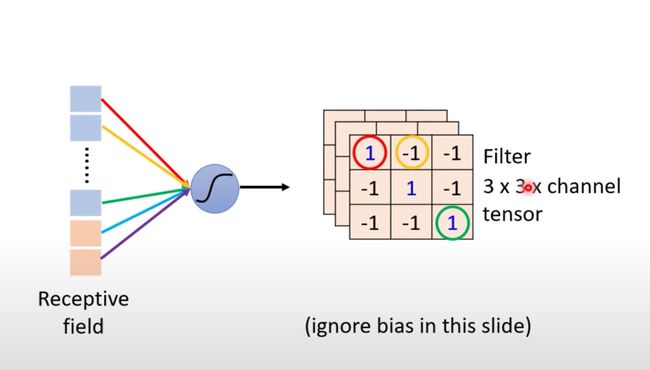
单个神经元将自己感受野内的内容拉直成3*3*3的27维向量
然后将27维的向量作为输入和权重W做內积,并加上偏置bias;这个隐藏层的结果作为下个隐藏层的输入。
也就是说,每个神经元只考虑值的感受野
感受野如何确定?
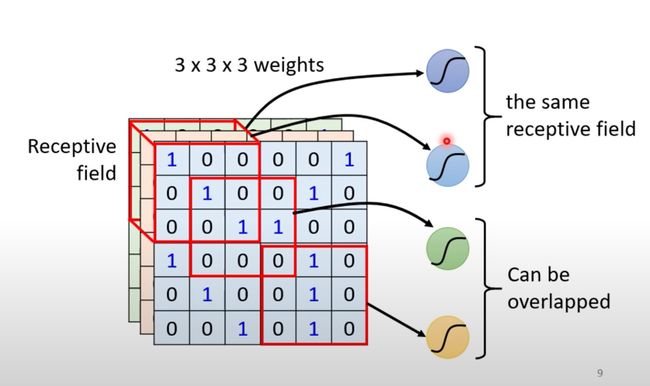
- 不同的感受野允许有重叠部分;
- 多个神经元Neuron共用同一个感受野;
感受野设置
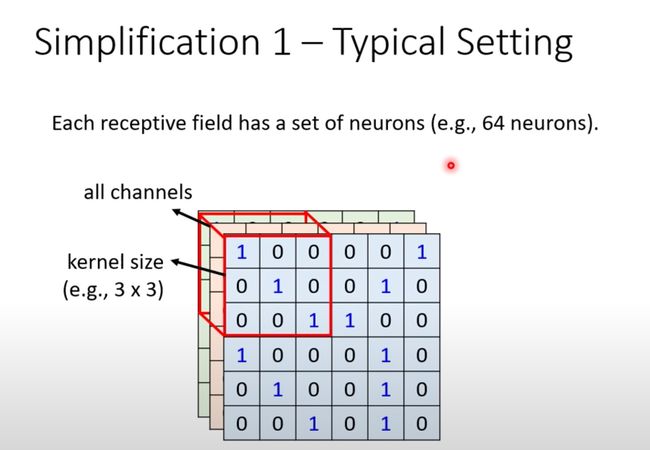
下面是一种经典的设置方式:查看全部通道channels
高和宽合起来叫做kernel_size,常见的设置是3*3
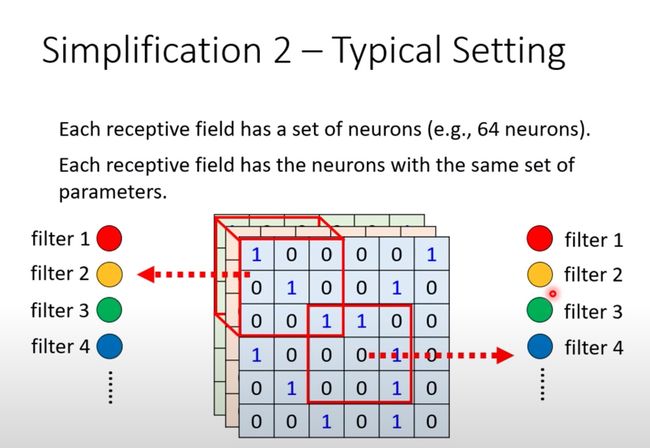
通常一个感受野不是只有一个神经元关注,通常是多个。比如常见的64个或者128个:
CNN概念-步长stride
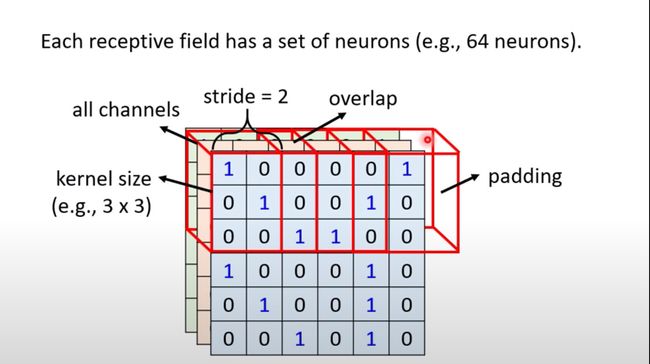
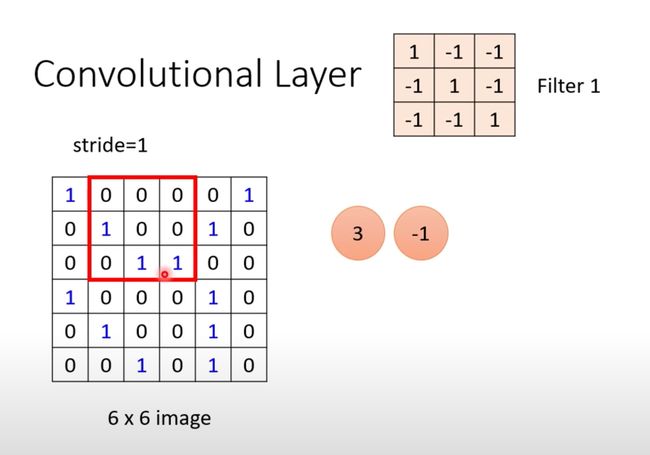
上面介绍的单个感受野,不同的感受野之间具有什么关系?将上面的红色部分向右移动stride个单位。
下面的图形中步长是2,移动2个单位。常见值是1或者2。
在移动的过程中发现不同的感受野之间有重叠部分(交集)。
CNN概念-填充padding
在感受野不断移动的过程中,可能出现超出边界的现象,如何处理?
使用Padding填充方法。常见的填充方法:
- 填充现有数据的均值
- 全部填充0
- 填充边界的相同值
除了水平移动,还可以垂直移动:
这样感受野能够扫描一张图片的全部区域。
CNN概念-参数共享
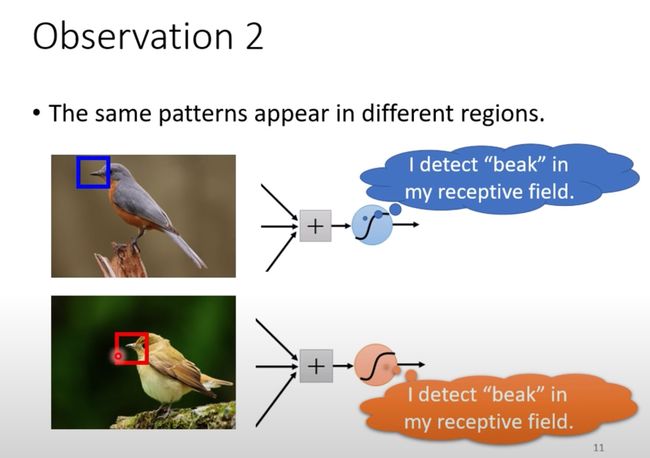
在不同的图片中,鸟嘴(某个特征)可能出现在不同的位置:
即便不同位置,但肯定是有某个神经元的感受野能够扫描到。
问题来了:相同的特征在不同的位置,需要在不同的位置使用不同的神经元吗?
李宏毅老师举例子:台湾大学教务处为什么会推大型的课程?假设每个院系都需要编程(机器学习)相关的课程,那么需要在每个院系都开设这门课吗?
回答:不需要。只需要开一门大课,让不同院系的学生都可以修课。避免重复
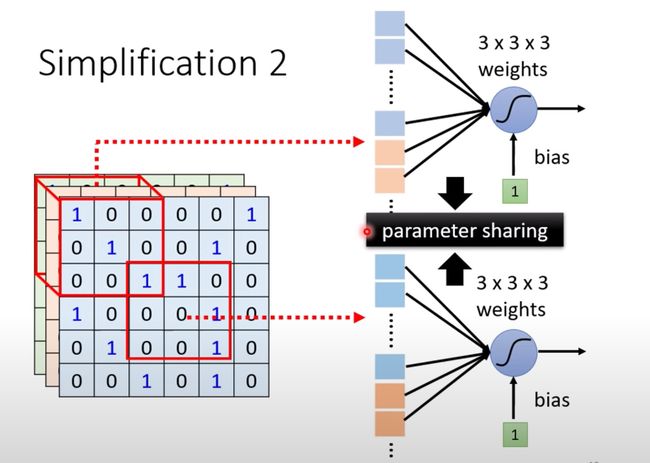
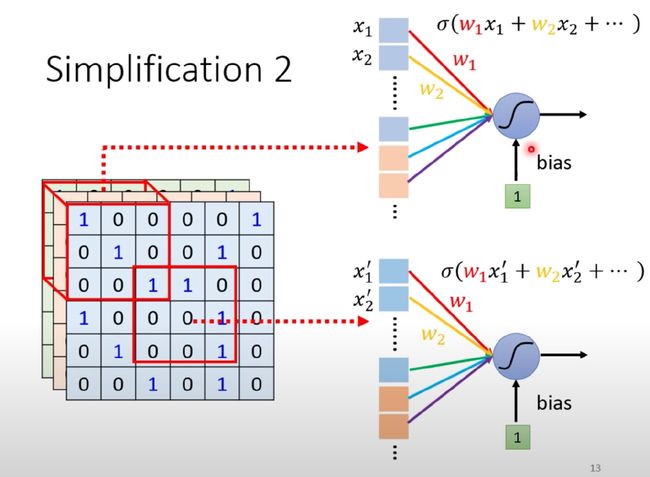
类比图像处理,在不同感受野的神经元上可以实现共享参数:
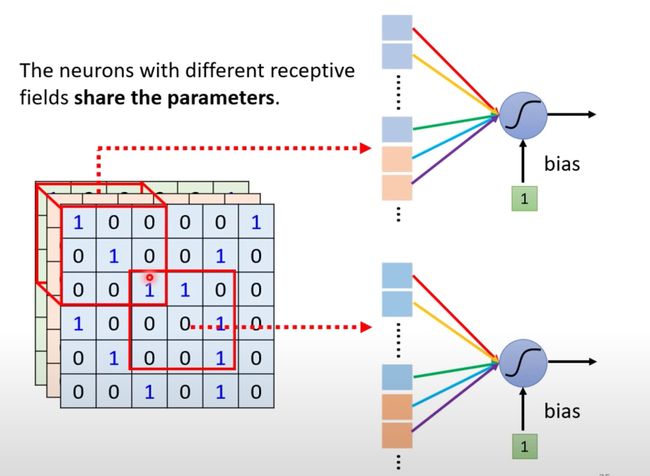
什么是共享参数?就是两个神经元(感受野区域不同)的参数是完全相同的:
注意右侧两个神经元不同输入下的颜色
虽然两个Neuron的weight相同,但是输入不同,也就是说最终输出是不同的:
CNN特点
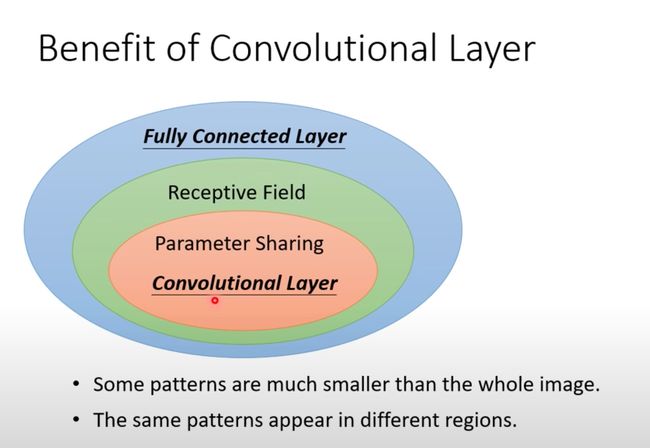
- Fully Connected Layer:全连接层;决定看整张图片还是部分
- Receptive Field:感受野,不需要全部图片,通过部分区域能够识别分类
- Parameter Sharing:参数共享;不同的Neuron之间共享相同的参数
- 当感受野 + 参数共享 之后就构成了卷积层Convolutional Layer
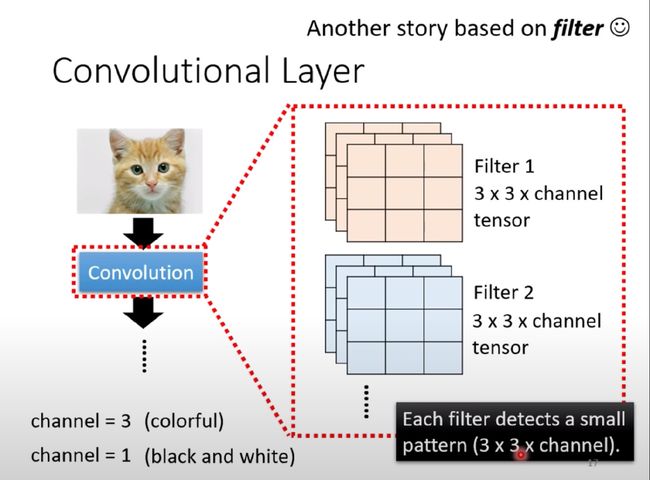
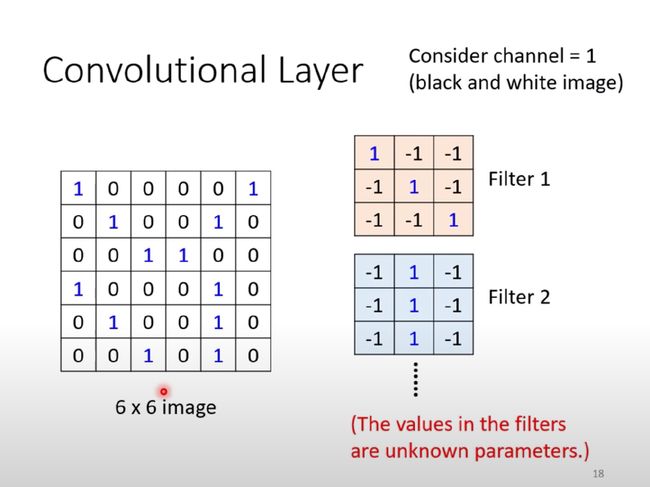
CNN概念-Filter过滤器
在卷积中存在不同的Filters,大小通常是3*3*chanels的
- 黑白:channels=1
- 彩色:channels=3
问题:每个Filter如何去图像中抓取某个特征pattern?
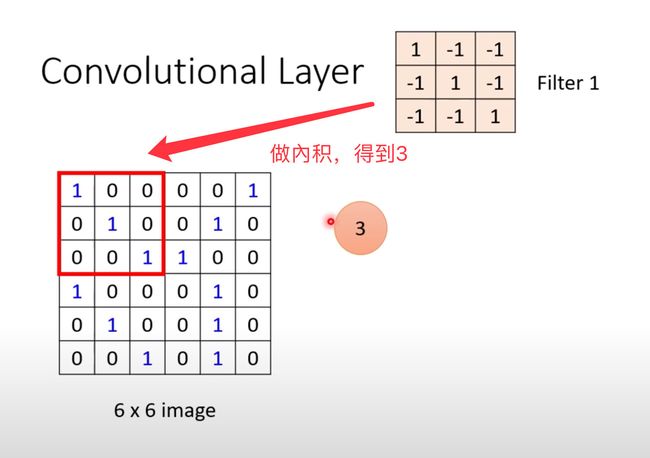
以Filter1为例:
依次向右和向下移动,得到不同的值:
在图片的不同位置上什么值最大?可以通过过滤器来判断:
CNN概念-特征图Feature Map
使用Filter2的结果:
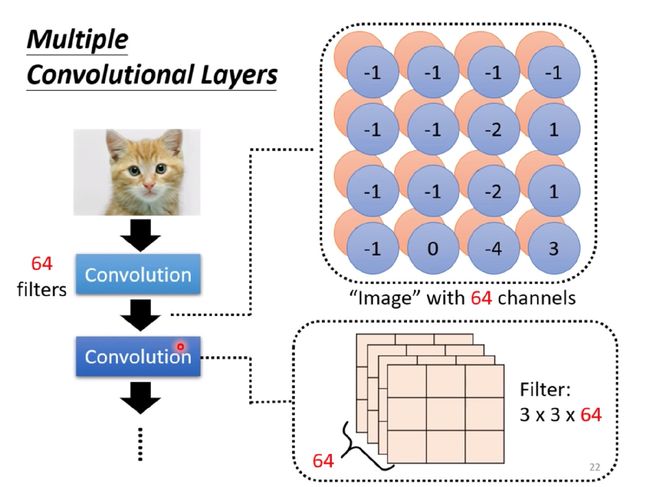
通过Filter和原图的內积得到的结果组成了特征图 Feature Map
这个Feature Map就可以看成是一张新的图片,具有64个channels(假设有64个Filters)
Convolution由来
对比两种不同方式下的颜色:在单个感受野生成的列向量对应的权重和Fliters中的数值是一一对应。
不同的神经元能够实现参数共享share parameters,从而作用域不同的感受野区域。
参数共享的过程其实就是一个Filter不断地扫过整张图片,这个过程也就是Convolution。
笔记:
- 不同的神经元Neuron能共享参数
- 共享的参数其实就是Filter
- Filter不断扫描图片的过程就是卷积
CNN概念-池化Pooling
在图片的处理,对图片的欠采样(缩放)不改变图片的本质:
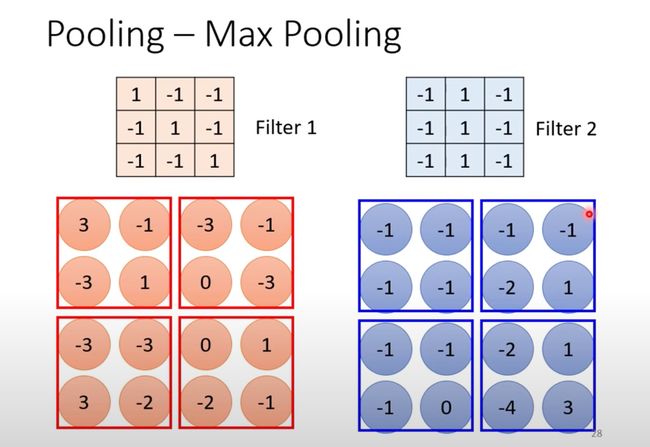
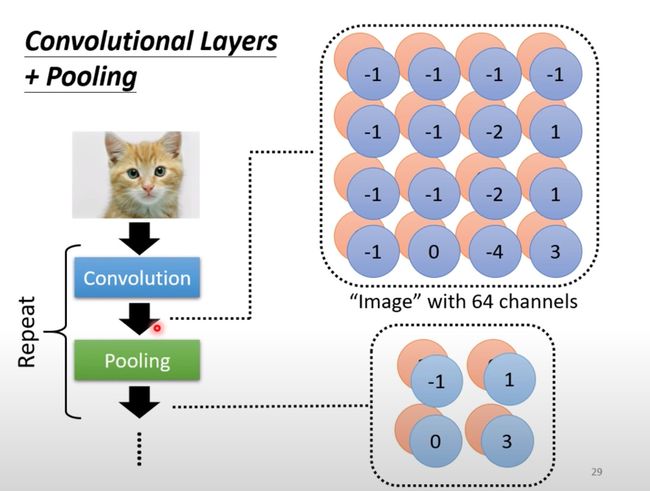
池化有多种方式,最常用的Max Pooling:
1、 假设我们通过Filter先生成了一个Feature Map特征图(可以看做一个新图片)
2、将特征图进行分组
下面是以2*2为例:
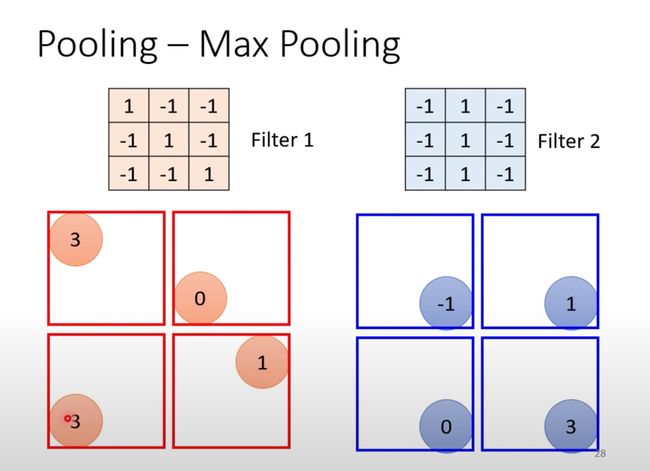
3、MaxPooling选择最大的值
所以一般在做完卷积之后会再做pooling的过程,将图片变小;二者一般是交替repeat使用:
池化的缺陷:池化的作用是将图片变小,做了subsampling之后减小运算量。当图片本身就细微的时候,池化削弱了原信息,导致网络可能表现的更差。
目前有些网路架构设计是纯Convolution,舍弃了Pooling。
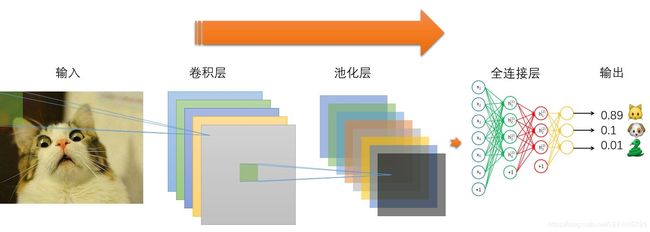
CNN全过程
- 对图片不断地进行卷积和池化
- 再经过Flatten:将矩阵拉直成一维向量
- 再将向量喂入全连接层FCL
- 最后加入一个softmax层,得到概率分布的结果,最后确定类别。
来自:李宏毅老师-卷积神经网络