概率论总结（一）：离散随机变量
目录：
- 离散随机变量定义及性质
- 常见的离散概率分布
- 伯努利分布
- 二项分布
- 几何分布
- 泊松分布 - 期望、矩、方差、标准差
- 多个随机变量的联合分布
- 条件
- 独立
骨骼图：
离散随机变量定义及性质
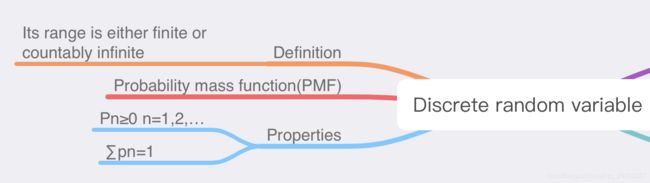
离散随机变量： 一个随机变量的值域为一个有限集合或最多为可数无限集合。
相关性质：
- 离散随机变量是实验结果的一个实值函数，但是它的取值范围只能是有限多个值或可数无限多个数。
- 一个离散随机变量有一个分布列，它对于随机变量的每一个取值，给出一个概率。
- 离散随机变量的函数也是一个离散随机变量，它的分布列可以从原随机变量的分布列得到。
分布列：
用分布列表示离散随机变量的取值概率，记为：
对于分布列：
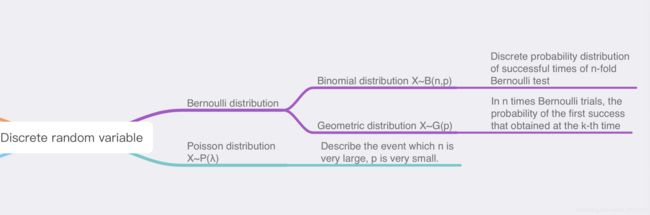
如第二个骨骼图，离散分布列包括伯努利分布（Bernoulli）和泊松分布（Poisson）。伯努利分布包括二项分布（Binomial distribution）和几何分布（Geometric distribution），二项分布是n重Bernoulli检验的离散概率分布，几何分布是在n次伯努利试验中，第k次获得首次成功的概率分布。
常见的离散概率分布
下面具体介绍这几个分布：
伯努利分布（Bernoulli distribution）
抛一枚硬币时，设正面朝上的概率为P，反面向上的概率为1-P，伯努利随机变量在实验结果为正面向上时取1，反面向上时取0。
伯努利随机变量常用来刻画具有两个实验结果的概率模型。
二项分布（Binomial distribution）
将一枚硬币抛n次，每抛一次，正面朝上的概率为P，反面向上的概率为1-P，而且每次抛都是独立的，令X为n次抛得到的正面向上的次数，称X为二项随机变量。
且：
几何分布（Geometric distribution）：
相同的抛硬币实验中，令X为连续的抛一枚硬币，直到第一次出现正面所需的次数。X就称为几何随机变量，因此X的分布列为：
泊松分布（Poisson distribution）：
设随机变量X的分布列由下式给出：
λ是刻画分布列的取正值的参数，X是泊松随机变量。
泊松分布用来描述出现概率很小的事件（即，n很大，P很小的情况）。
期望、矩、方差、标准差
期望
X的期望就是X的所有取值相对于它的概率的加权平均。
特别的，当随机变量的分布列具有对称中心时，这个对称中心必定为这个对称随机变量的均值。
矩：
方差
（日本教材中，方差就写作分散。）
标准差：
（Special）：
例1：
随机变量的函数的期望：
将它应用于方差，即将(X-E(X))^2看作X的函数，则方差可以表示为：
当然，我们可以用矩表达方差：
证明：
相似地，对于X的n阶矩，有：
因此上例可以这样解：
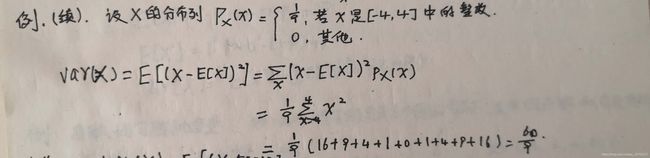
二项随机变量的均值和方差：
若X～B(n,p):
解释一下最后一个等式：
几何随机变量的均值和方差：
证明：
泊松分布的均值和方差：
证明：
离散均匀随机变量的均值和方差：
按定义，离散均匀随机变量的取值范围由相邻的整数所组成的有限集， 而取每个整数的概率都是相等的，它的分布列为：
其中，a、b为两个整数，a
为计算X的方差，先考虑a=1，b=n的简单情况。
利用归纳法可得：
样本均值的期望和方差
例：（总统的支持率）设随机选取n个选民，Xi代表第i个选民的态度。则：
将X1,…,Xn看作独立同分布的伯努利随机变量。均值为p,方差为p(1-p)。将p认为是支持总统的概率，且调查得到的平均反应Sn称为样本均值。
上式即使Xi不是伯努利随机变量，var(Sn)=var(X)/n仍然成立。
多个随机变量的联合分布
多个随机变量是指在同一个实验结果之下产生的多个随机变量，它们涉及的样本空间和概率是相同的。
现假设有两个随机变量X和Y，它们的取值概率可以用联合分布列刻画，并且用Px,y表示：
可以利用X和Y的联合分布列计算出X或Y的分布列：
称Px(X)或PY(Y)为边缘分布列。
多个随机变量的函数
多个随机变量的情况下可以构造出新的随机变量，特别的，从二元函数Z=g(X,Y)可以确定一个新的随机变量，这个新的随机变量的分布列：
当g是形如aX+bY+c的线性函数时，有：
E[aX+bY+c]=aE[X]+bE[Y]+c
三个随机变量的情况如下：
条件
条件概率：
设某试验中有两个随机变量X和Y。
若Y已取定，
。
有：
且：
与联合分布的关系：
条件期望：
设X和Y为某一试验中的两个随机变量。
1.设A为某事件，p(A)>0，随机变量X在给定A发生的条件下的条件期望为：
对于函数g(x)，有：
2.在给定Y=y的条件下，X的条件期望由下式定义：
3.
独立：
对一切x和y成立，随机变量X和Y称为相互独立的随机变量。
在给定事件A的条件下（P(A)必须大于0）也可以定义两个随机变量的条件独立性。
若满足P(X=x,Y=y|A)=P(X=x|A)P(Y=y|A)对于一切x和y成立。则称随机变量X和Y在给定正概率事件A的条件下式条件独立的。
并且：E[XY]=E[X]E[Y];var(X+Y)=var(X)+var(Y)
随机变量加上一个常数后，其方差保持不变。