金融风控实战——信贷准入模型
import pandas as pd
from sklearn.metrics import roc_auc_score,roc_curve,auc
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import numpy as np
import math
import xgboost as xgb
import toad
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve,auc
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
###################### PlotKS ##########################
def plot_ks( labels,preds, n, asc):
# preds is score: asc=1
# preds is prob: asc=0
pred = preds # 预测值
bad = labels # 取1为bad, 0为good
ksds = pd.DataFrame({'bad': bad, 'pred': pred})
ksds['good'] = 1 - ksds.bad
if asc == 1:
ksds1 = ksds.sort_values(by=['pred', 'bad'], ascending=[True, True])
elif asc == 0:
ksds1 = ksds.sort_values(by=['pred', 'bad'], ascending=[False, True])
ksds1.index = range(len(ksds1.pred))
ksds1['cumsum_good1'] = 1.0*ksds1.good.cumsum()/sum(ksds1.good)
ksds1['cumsum_bad1'] = 1.0*ksds1.bad.cumsum()/sum(ksds1.bad)
if asc == 1:
ksds2 = ksds.sort_values(by=['pred', 'bad'], ascending=[True, False])
elif asc == 0:
ksds2 = ksds.sort_values(by=['pred', 'bad'], ascending=[False, False])
ksds2.index = range(len(ksds2.pred))
ksds2['cumsum_good2'] = 1.0*ksds2.good.cumsum()/sum(ksds2.good)
ksds2['cumsum_bad2'] = 1.0*ksds2.bad.cumsum()/sum(ksds2.bad)
# ksds1 ksds2 -> average
ksds = ksds1[['cumsum_good1', 'cumsum_bad1']]
ksds['cumsum_good2'] = ksds2['cumsum_good2']
ksds['cumsum_bad2'] = ksds2['cumsum_bad2']
ksds['cumsum_good'] = (ksds['cumsum_good1'] + ksds['cumsum_good2'])/2
ksds['cumsum_bad'] = (ksds['cumsum_bad1'] + ksds['cumsum_bad2'])/2
# ks
ksds['ks'] = abs(ksds['cumsum_bad'] - ksds['cumsum_good'])
ksds['tile0'] = range(1, len(ksds.ks) + 1)
ksds['tile'] = 1.0*ksds['tile0']/len(ksds['tile0'])
qe = list(np.arange(0, 1, 1.0/n))
qe.append(1)
qe = qe[1:]
ks_index = pd.Series(ksds.index)
ks_index = ks_index.quantile(q = qe)
ks_index = np.ceil(ks_index).astype(int)
ks_index = list(ks_index)
ksds = ksds.loc[ks_index]
ksds = ksds[['tile', 'cumsum_good', 'cumsum_bad', 'ks']]
ksds0 = np.array([[0, 0, 0, 0]])
ksds = np.concatenate([ksds0, ksds], axis=0)
ksds = pd.DataFrame(ksds, columns=['tile', 'cumsum_good', 'cumsum_bad', 'ks'])
ks_value = ksds.ks.max()
ks_pop = ksds.tile[ksds.ks.idxmax()]
print ('ks_value is ' + str(np.round(ks_value, 4)) + ' at pop = ' + str(np.round(ks_pop, 4)))
# chart
plt.plot(ksds.tile, ksds.cumsum_good, label='good',
color='blue', linestyle='-', linewidth=1)
plt.plot(ksds.tile, ksds.cumsum_bad, label='bad',
color='red', linestyle='-', linewidth=1)
plt.plot(ksds.tile, ksds.ks, label='ks',
color='green', linestyle='-', linewidth=1)
plt.axvline(ks_pop, color='gray', linestyle='--')
plt.axhline(ks_value, color='green', linestyle='--')
plt.axhline(ksds.loc[ksds.ks.idxmax(), 'cumsum_good'], color='blue', linestyle='--')
plt.axhline(ksds.loc[ksds.ks.idxmax(),'cumsum_bad'], color='red', linestyle='--')
plt.title('KS=%s ' %np.round(ks_value, 4) +
'at Pop=%s' %np.round(ks_pop, 4), fontsize=15)
plt.xlabel('Threshold')
plt.ylabel('TPR/FPR')
plt.legend(loc='best')
return ks_value
####################### over ##########################
def plot_roc(labels, predict_prob):
false_positive_rate,true_positive_rate,thresholds=roc_curve(labels, predict_prob)
roc_auc=roc_auc_score(labels,predict_prob)
plt.title('ROC')
plt.plot(false_positive_rate, true_positive_rate,'b',label='AUC = %0.4f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')
plt.show()
# 加载数据
data_all = pd.read_csv("scorecard.txt")
# 开发样本、验证样本与时间外样本
dev = data_all[(data_all['samp_type'] == 'dev')]
val = data_all[(data_all['samp_type'] == 'val') ]
off = data_all[(data_all['samp_type'] == 'off') ]
# 指定不参与训练列名
ex_lis = ['uid', 'samp_type', 'bad_ind']
# 参与训练列名
ft_lis = list(data_all.columns)
for i in ex_lis:
ft_lis.remove(i)
这里使用了开源的toad来实施,但是当数据量很大的时候建议还是从pyspark或者python+hive的形式,否则单机处理超大量的数据非常慢效率也低
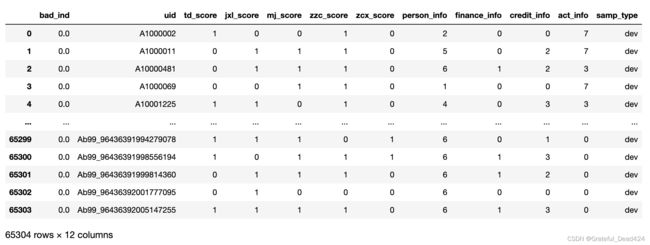
这里我们先对所有的数据进行概览,需要注意的是,原始数据处理起来往往是比较简单但是非常繁琐的,一般原始的数据是包含多张表的,包括了用户的基本信息、用户的征信报告、用户的app行为(例如用户在拍拍贷平台上的点击情况、登陆情况等等)、用户的其它信息等,我们要做的事情,就是对每一张表都进行原始数据的清洗和处理,包括了缺失值的推理、删除、插补,异常值的去除、校证,原始数据的错误检测等等
data_all
toad.detector.detect(data_all)
缺失值处理
data_all.isnull().sum()
#bad_ind 0
#td_score 0
#jxl_score 0
#mj_score 0
#rh_score 0
#zzc_score 0
#zcx_score 0
#person_info 0
#finance_info 0
#credit_info 0
#act_info 0
#samp_type 0
#dtype: int64
原始数据未存在缺失值
异常值处理
data_all.info()
#box_data = ft_lis
for col in ft_lis:、
plt.figure(figsize=(5,5))
plt.boxplot(data_all[col])
可以看到连续特征之间虽然存在一些孤立点,但是所有的数据其分布的区间范围都在0~1之间,并不存在量纲上的差异,此时并不需要什么异常值处理,只有当量纲上存在较大差异的时候才需要做一些异常值处理
data_all.samp_type.value_counts(1)
#dev 0.681627
#off 0.166743
#val 0.151629
#Name: samp_type, dtype: float64
plt.figure(figsize=(15,15))
sns.heatmap(data_all.corr())
这里我们选择去掉缺失率超过0.7或iv值小于0.03,或相关性超过0.7的特征,当然,具体的缺失率、iv、相关性的阈值没有一个固定的标准,一般来说,对于上述的处理我们要同时考虑模型的排序性、模型的稳定性、模型的复杂度、可解释性等,一个通用的思路就是,在保证模型不损失精度或者损失很小的精度的情况下尽量make it simple。
data_all.columns
#Index(['bad_ind', 'uid', 'td_score', 'jxl_score', 'mj_score', 'rh_score',
# 'zzc_score', 'zcx_score', 'person_info', 'finance_info', 'credit_info',
# 'act_info', 'samp_type'],
# dtype='object')
需要注意,toad内部自动对特征进行了分箱,所以没有一个显式的分箱过程
特征的iv\ks\psi值计算,前期当特征数量过大,样本数量过多的情况下常通过这种方式来快速进行过滤式特征筛选(iv小于0.03删除,ks小于0.02删除)
cols=list(data_all.columns)
cols.remove('bad_ind')
cols.remove('samp_type')
toad.IV(dev[cols],dev.bad_ind).T
ks=pd.DataFrame(columns=['features','ks'])
ks.features=cols
tp=[]
for col in cols:
tp.append(toad.metrics.KS(dev[col],dev.bad_ind))
ks['ks']=tp
ks
toad.metrics.PSI(dev,off)
#bad_ind 0.000790
#uid 0.000000
#td_score 0.000000
#jxl_score 0.000000
#mj_score 0.000000
#rh_score 0.000000
#zzc_score 0.000000
#zcx_score 0.000000
#person_info 0.127833
#finance_info 0.140048
#credit_info 0.130314
#act_info 0.372135
#samp_type 0.000000
#dtype: float64
dev_slct1, drop_lst= toad.selection.select(dev, dev['bad_ind'],
empty=0.7, iv=0.03,
corr=0.7,
return_drop=True,
exclude=ex_lis)
print("keep:", dev_slct1.shape[1],
"drop empty:", len(drop_lst['empty']),
"drop iv:", len(drop_lst['iv']),
"drop corr:", len(drop_lst['corr']))
#keep: 12 drop empty: 0 drop iv: 1 drop corr: 0
这里需要补充一下woe和iv的背景知识
woe和iv
W O E i = ln ( Bad i Bad T / Good i Good T ) = ln ( Bad i Bad T ) − ln ( Good i Good T ) W O E_{i}=\ln \left(\frac{\operatorname{Bad}_{i}}{\operatorname{Bad}_{T}} / \frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right)=\ln \left(\frac{\operatorname{Bad}_{i}}{\operatorname{Bad}_{T}}\right)-\ln \left(\frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right) WOEi=ln(BadTBadi/GoodTGoodi)=ln(BadTBadi)−ln(GoodTGoodi)
一般来说,我们在对变量进行woe编码的时候,要进行分箱处理,然后每一个箱子计算出一个woe值,计算方法也很简单,就是用这个箱子中坏客户数量/总的坏客户数量 然后除以 这个箱子中好客户的数量除以总的好客户数量,变换一下,也可以通过 这个箱子中坏客户数量/这个箱子中好客户数量 然后除以 总的好客户数量/总的坏客户数量,此时公式转化为: W O E i = ln ( B a d i B a d T / Good i Good T ) = ln ( Bad i Good i ) − ln ( B a d T G o o d T ) W O E_{i}=\ln \left(\frac{B a d_{i}}{B a d_{T}} / \frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right)=\ln \left(\frac{\operatorname{Bad}_{i}}{\operatorname{Good}_{i}}\right)-\ln \left(\frac{B a d_{T}}{G o o d_{T}}\right) WOEi=ln(BadTBadi/GoodTGoodi)=ln(GoodiBadi)−ln(GoodTBadT)此时可以理解为:每个分箱里的坏好比(Odds)相对于总体的坏好比之间的差异性。这里,woe的计算引入了一种很重要的思想,即 随机意义,例如我们在graph领域,会以random graph为基准,去计算某一个特定的graph是否有显著的意义,在shap的计算中,也会以random value作为基准去计算特征值的shap value,在louvain中也会以random connect作为benchmark来计算节点之间的合并是否能够产生显著的统计意义,这是机器学习领域中一种非常常用的方法和技巧,在woe的计算中,以全量用户的好坏客户占比作为随机意义下的占比情况,然后将箱子的好坏客户占比与其进行对比,计算的结果越大则显著性越明显,woe值越大
那么woe在评分卡中有哪些作用呢?
- 1、处理缺失值:当数据源没有100%覆盖时,那就会存在缺失值,此时可以把null单独作为一个分箱。这点在分数据源建模时非常有用,可以有效将覆盖率哪怕只有20%的数据源利用起来。
- 2、处理异常值:当数据中存在离群点时,可以把其通过分箱离散化处理,从而提高变量的鲁棒性(抗干扰能力)。例如,age若出现200这种异常值,可分入“age > 60”这个分箱里,排除影响。
- 3、业务解释性:我们习惯于线性判断变量的作用,当x越来越大,y就越来越大。但实际x与y之间经常存在着非线性关系,此时可经过WOE变换。
需要注意,woe的这些作用主要是针对与逻辑回归这样的传统评分卡模型起作用,对于xgboost这类,其实很多时候不一定要引入woe编码,woe的具体计算如下:
举个例子: 假设我们的原始特征为[1,1.1.5,3,5.5,7,10]对应的用户标签为[0,0,1,1,0,0,0,1],则我们要先对特征进行分箱,常见的分箱方法包括等宽、等频、卡方、决策树分箱等方法,假设我们按照[-inf,2],[2,5],[9,inf],则分箱之后的结果为[0,0,0,1,1,1,2,2],总的好坏客户比例为3/8=0.375,“0”箱用户的坏客户比例为 1/2=0.5,则起woe值为ln(0.5/0.375)=0.7066950526114237
同时需要注意,如果分箱中的结果,如好客户为0个或者坏客户为0个,这个时候ln都无法正常计算,此时有两个思路:
-
1、分箱的效果这么好,箱子中全是好客户或者坏客户,此时这个特征可以考虑直接作为规则前置到我们的风控引擎中的规则中去;
-
2、拉普拉斯平滑,直接对分母和分子加上一个小常数例如1或者0.001之类的
IV的计算公式定义如下,其可认为是WOE的加权和。
I V i = ( Bad i Bad T − Good i Good T ) ∗ W O E i = ( B a d i Bad T − Good i Good T ) ∗ ln ( Bad i Bad T / Good i Good T ) I V = ∑ i = 1 n I V i \begin{gathered} I V_{i}=\left(\frac{\operatorname{Bad}_{i}}{\operatorname{Bad}_{T}}-\frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right) * W O E_{i} \\ =\left(\frac{B a d_{i}}{\operatorname{Bad}_{T}}-\frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right) * \ln \left(\frac{\operatorname{Bad}_{i}}{\operatorname{Bad}_{T}} / \frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right) \\ I V=\sum_{i=1}^{n} I V_{i} \end{gathered} IVi=(BadTBadi−GoodTGoodi)∗WOEi=(BadTBadi−GoodTGoodi)∗ln(BadTBadi/GoodTGoodi)IV=i=1∑nIVi这里权重的定义为 箱子坏客户数量/总的坏客户数量-箱子好客户数量/总的好客户数量,主要原因在于,我们分箱的结果可能导致的问题是每一个箱子的用户数量不相同,有的箱子可能10000个人,有的箱子100个人,但是概率的计算却与样本数量无关,因此我们通过引入上述的权重的概念来进行惩罚,这样箱子里用户数量少的箱子其权重就会比较小,而用户数量大的箱子其权重机会比较大,从而较好的解决了箱子里用户数量大小不同的问题,这样计算出来的特征的IV值才能真实反映特征本身的区分能力;
end
这里我们使用卡方分箱来进行分箱,关于分箱的问题,大家有空可以参考我之前写的分箱方法总结: https://zhuanlan.zhihu.com/p/68865422
下面使用的是卡方分箱
# 得到切分节点
combiner = toad.transform.Combiner()
combiner.fit(dev_slct1, dev_slct1['bad_ind'], method='chi',
min_samples=0.05, exclude=ex_lis)
# 导出箱的节点
bins = combiner.export()
print(bins)
#{'td_score': [0.7989831262724624], 'jxl_score': [0.4197048501965005], 'mj_score': [0.3615303943747963], 'zzc_score': [0.4469861520889339], 'zcx_score': [0.7007847486465795], 'person_info': [-0.2610139784946237, -0.1286774193548387, -0.0537175627240143, 0.013863440860215, 0.0626602150537634, 0.078853046594982], 'finance_info': [0.0476190476190476], 'credit_info': [0.02, 0.04, 0.11], 'act_info': [0.1153846153846154, 0.141025641025641, 0.1666666666666666, 0.2051282051282051, 0.2692307692307692, 0.358974358974359, 0.3974358974358974, 0.5256410256410257]}
# 根据节点实施分箱
dev_slct2 = combiner.transform(dev_slct1)
val2 = combiner.transform(val[dev_slct1.columns])
off2 = combiner.transform(off[dev_slct1.columns])
dev_slct2
# 分箱后通过画图观察
from toad.plot import bin_plot, badrate_plot
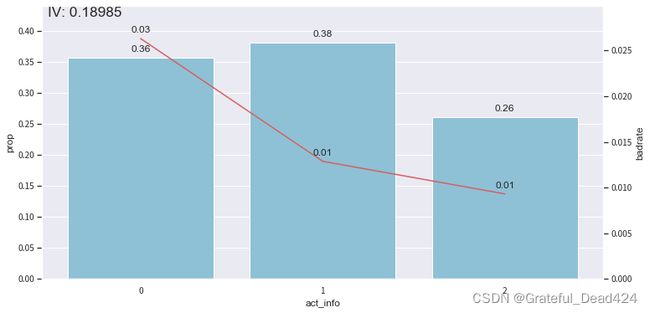
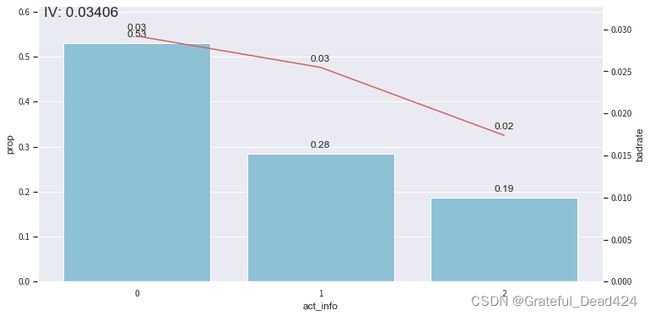
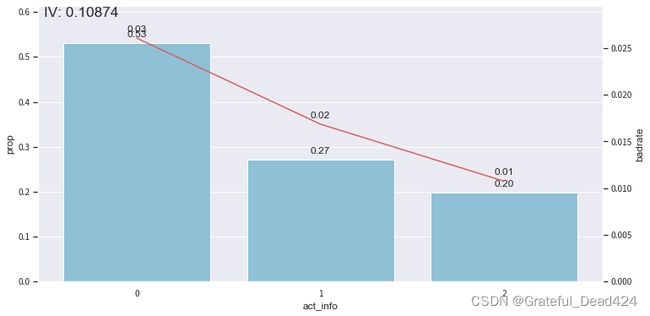
bin_plot(dev_slct2, x='act_info', target='bad_ind')
bin_plot(val2, x='act_info', target='bad_ind')
bin_plot(off2, x='act_info', target='bad_ind')
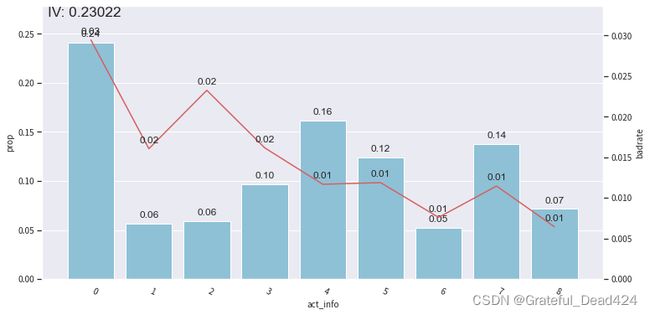
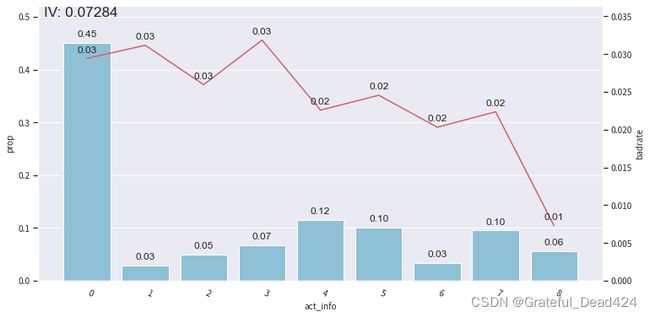
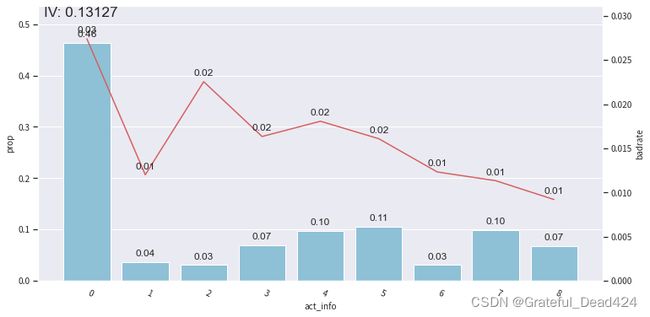
可以看到,经过分箱和woe编码之后,我们的bad rate整体呈现出较好的线性趋势,
注意:关于特征是否要处理成线性的。。。说老实话主要是为了逻辑回归模型的解释性问题,逻辑回归认为变量之间是完全独立的,因此我们通过分箱和woe编码尽量将特征之间的相关性降下来,除此之外,这样我们就可以固定n-1个特征,然后在第n个特征上进行增大或者减少,观察用户评分的变化情况,从而获得可解释性,但是当变量与评分结果之间的关系是非线性的,例如年龄和评分之间一般是一个n型分布,即年龄在某个区间和评分之间是正相关的,在另一个区间是负相关的,主要是因为年龄小则一般收入水平低,不稳定,当人到中年,一般事业有一定成就,收入和稳定性都大大提高,而年龄再大,面临退休等问题,收入会降低,从而使得用户的偿还能力下降
因此,总而言之,这种线性的处理主要是为了解释性的问题,换句话说,在不是很care模型解释性或者不需要这么“直白”的解释性的场景下,我们并不太需要这样来处理
bins['act_info']
#[0.1153846153846154,
# 0.14102564102564102,
# 0.16666666666666666,
# 0.20512820512820512,
# 0.2692307692307692,
# 0.35897435897435903,
# 0.3974358974358974,
# 0.5256410256410257]
adj_bin = {'act_info': [0.16666666666666666,0.35897435897435903,]}
combiner.set_rules(adj_bin)
dev_slct3 = combiner.transform(dev_slct1)
val3 = combiner.transform(val[dev_slct1.columns])
off3 = combiner.transform(off[dev_slct1.columns])
# 画出Bivar图
bin_plot(dev_slct3, x='act_info', target='bad_ind')
bin_plot(val3, x='act_info', target='bad_ind')
bin_plot(off3, x='act_info', target='bad_ind')
data = pd.concat([dev_slct3,val3,off3], join='inner')
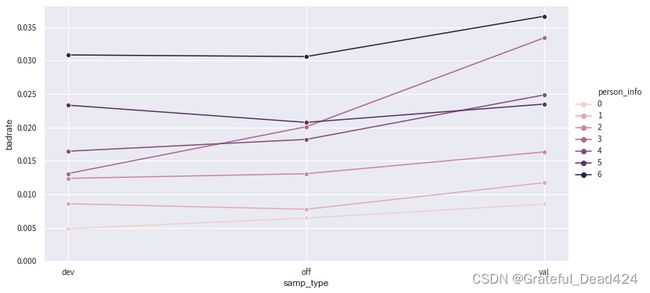
badrate_plot(data, x='samp_type', target='bad_ind', by='person_info')
t = toad.transform.WOETransformer()
dev_slct3_woe = t.fit_transform(dev_slct3, dev_slct3['bad_ind'],
exclude=ex_lis)
val_woe = t.transform(val3[dev_slct3.columns])
off_woe = t.transform(off3[dev_slct3.columns])
data = pd.concat([dev_slct3_woe, val_woe, off_woe])
data
psi_df = toad.metrics.PSI(dev_slct3_woe, val_woe).sort_values(0)
psi_df = psi_df.reset_index()
psi_df = psi_df.rename(columns = {'index': 'feature', 0: 'psi'})
psi_df
psi_013 = list(psi_df[psi_df.psi<0.13].feature)
for i in ex_lis:
if i in psi_013:
pass
else:
psi_013.append(i)
data = data[psi_013]
dev_woe_psi = dev_slct3_woe[psi_013]
val_woe_psi = val_woe[psi_013]
off_woe_psi = off_woe[psi_013]
print(data.shape)
#(95806, 11)
dev_woe_psi2, drop_lst = toad.selection.select(dev_woe_psi,
dev_woe_psi['bad_ind'],
empty=0.6,
iv=0.001,
corr=0.5,
return_drop=True,
exclude=ex_lis)
print("keep:", dev_woe_psi2.shape[1],
"drop empty:", len(drop_lst['empty']),
"drop iv:", len(drop_lst['iv']),
"drop corr:", len(drop_lst['corr']))
#keep: 7 drop empty: 0 drop iv: 4 drop corr: 0
基于aic的逐步回归进行双向特征选择
补充:逐步回归
在了解逐步回归之前首先要理解aic和bic的概念:
1、AIC=-2 ln(L) + 2 k 中文名字:赤池信息量 akaike information criterion,赤池信息量准则,即Akaike information criterion、简称AIC,是衡量统计模型拟合优良性的一种标准,是由日本统计学家赤池弘次创立和发展的。赤池信息量准则建立在熵的概念基础上;
2、BIC=-2 ln(L) + ln(n)* k 中文名字:贝叶斯信息量 bayesian information criterion BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
可以看到,aic和bic的概念略类似于L正则化但是和L正则化在公式上是不一样的,需要注意,上面公式中的L表示的就是似然函数,k是特征的数量,n是样本的数量,ln(L)衡量的是模型的拟合程度。
一般而言,当模型复杂度提高(k增大即特征数量增加)时,似然函数L也会增大,从而使AIC或BIC变小,但是k过大时,似然函数增速减缓,导致AIC或者BIC增大,特征的数量和二者的关系呈现一个U型,模型过于复杂容易造成过拟合现象。我们的目标是选取AIC或者BIC最小的模型,不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型特征数量尽可能少,有助于降低过拟合的可能性。
逐步回归的思路主要是三种,一种是前向,一种的是后向,一种的双向,我们下面用的是双向,思路很简单,对于前向的逐步回归来说,我们每次是选择一个特征入模,构建lr模型,计算aic或者bic,然后再引入一个特征入模,计算aic和bic,如果新的特征和原始特征存在很强的共线性,则对于模型来说,并没有增加新的信息,那么其代价函数L并不会增大,即模型的拟合优度不会提高,但是引入了新的特征之后K增大了,因此会导致aic增大,则新特征不会加入进来进行删除,如果引入的新特征和原始特征共线性很低并且对于最终的预测具有贡献度则往往L会减少,模型拟合优度上升,cover了K增大带来的影响,而后向逐步回归则是反过来,先使用所有特征,计算一个aic或者bic,然后随机删除一个特征,再次计算aic或者bic,比较两次计算的结果差异;如果是双向的逐步回归则比较繁琐一些,整体过程是先走后向,即用全部特征建模,然后删除特征,但是每次删除一个特征之后又会依次加入之前其它的已经被删除的特征看看模型的aic或者bic是否提升,因此双向的计算复杂度是要更高的,但是也可以更加准确的进行特征选择
end
dev_woe_psi_stp = toad.selection.stepwise(dev_woe_psi2,
dev_woe_psi2['bad_ind'],
exclude=ex_lis,
direction='both',
criterion='aic',
estimator='ols',
intercept=False)
val_woe_psi_stp = val_woe_psi[dev_woe_psi_stp.columns]
off_woe_psi_stp = off_woe_psi[dev_woe_psi_stp.columns]
data = pd.concat([dev_woe_psi_stp, val_woe_psi_stp, off_woe_psi_stp])
print(data.shape)
#(95806, 6)
下面我们对转换之后的数据进行lr建模
data.bad_ind.value_counts()
#0.0 94008
#1.0 1798
#Name: bad_ind, dtype: int64
dev = data[data['samp_type']=='dev'] #训练集
val = data[data['samp_type']=='val'] #验证集
off = data[data['samp_type']=='off' ] #跨时间验证集
import gc
from sklearn.model_selection import StratifiedKFold
cols=['credit_info','act_info','person_info']
X=dev
y=dev.bad_ind.astype(int)
folds = StratifiedKFold(n_splits=5)
splits = folds.split(X, y)
y_oof=np.zeros(X.shape[0])
auc=0.0
ks=0.0
for fold_n, (train_index, valid_index) in enumerate(splits):
X_train, X_valid = X[cols].iloc[train_index], X[cols].iloc[valid_index]
y_train, y_valid = y.iloc[train_index], y.iloc[valid_index]
clf = LogisticRegression(C=0.01,)# class_weight='balanced')
clf.fit(X_train,y_train)
y_pred_valid = clf.predict_proba(X_valid)[:,1]
fpr_val,tpr_val,_ = roc_curve(y_valid, y_pred_valid)
y_oof[valid_index] = y_pred_valid
print(f"Fold {fold_n + 1} | AUC: {roc_auc_score(y_valid, y_pred_valid)}")
print(f"Fold {fold_n + 1} | KS: {abs(fpr_val - tpr_val).max()}")
print('\n')
ks+=abs(fpr_val - tpr_val).max()/5
auc += roc_auc_score(y_valid, y_pred_valid) / 5
del X_train, X_valid, y_train, y_valid;gc.collect()
print(f"Mean AUC = {auc}")
print(f"Mean KS = {ks}")
print(f"Out of folds AUC = {roc_auc_score(y, y_oof)}")
fpr_val,tpr_val,_ = roc_curve(y, y_oof)
print(f"Out of folds KS = {abs(fpr_val - tpr_val).max()}")
#Fold 1 | AUC: 0.7652374798823047
#Fold 1 | KS: 0.4061199225366048
#
#
#Fold 2 | AUC: 0.7630162942798281
#Fold 2 | KS: 0.43028547168643977
#
#
#Fold 3 | AUC: 0.7969937043050095
#Fold 3 | KS: 0.465547550524499
#
#
#Fold 4 | AUC: 0.7862038018801037
#Fold 4 | KS: 0.4462945856169717
#
#
#Fold 5 | AUC: 0.7452392450802914
#Fold 5 | KS: 0.40292246341919935
#
#
#Mean AUC = 0.7713381050855075
#Mean KS = 0.43023399875674295
#Out of folds AUC = 0.7649529570873976
#Out of folds KS = 0.40522693202845955
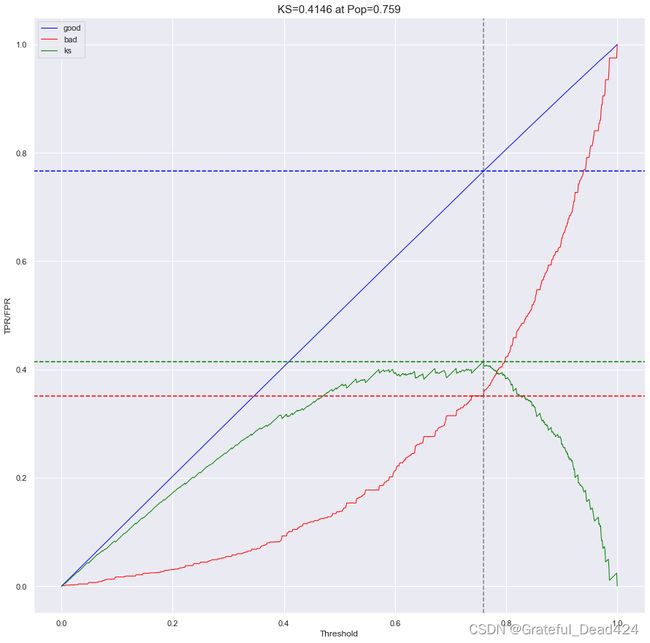
plt.figure(figsize=(15,15))
plot_ks(y,y_oof,n=1000,asc=True)
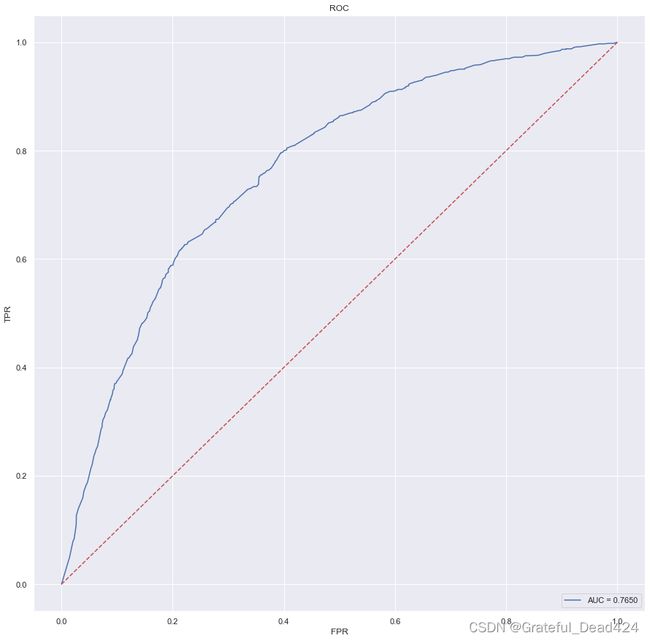
plt.figure(figsize=(15,15))
plot_roc(y,y_oof)
dev = data[data['samp_type']=='dev'] #训练集
val = data[data['samp_type']=='val'] #验证集
off = data[data['samp_type']=='off' ] #跨时间验证集
from toad.metrics import KS, F1, AUC
clf = LogisticRegression(C=0.01,)# class_weight='balanced')
clf.fit(dev[cols],dev.bad_ind)
prob_dev = clf.predict_proba(dev[cols])[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols])[:,1]
print('验证集')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
#训练集
#F1: 0.019909118234701276
#KS: 0.4125267446900638
#AUC: 0.7705257681805365
#跨时间
#F1: 0.034845443596949015
#KS: 0.36571144707613573
#AUC: 0.7283522508927651
#跨时间
#F1: 0.022255782529210715
#KS: 0.38701001672571844
#AUC: 0.7466196863109424
#模型PSI: 0.3409166738610026
我们可以进行一些简单的调参来观察模型效果的变化
for c in [0.005,0.01,0.05,0.1,0.5,1]:
for class_weight in ['balanced',3,5,10,None]:
print('C='+str(c))
print('class_weight='+str(class_weight))
clf = LogisticRegression(C=c,class_weight=class_weight)
clf.fit(dev[cols],devv.bad_ind)
prob_dev = clf.predict_proba(dev[cols])[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
print('============================================================================')
可以看到,模型整体的psi是很高的的,稳定性不好,一般来说模型需要上线,则auc和ks需要满足一定的要求,具体的要求不同机构的要求可能不一样,但是基本上至少要0.8以上才会有比较好的效果,并且三个数据集的auc和ks的差异要控制在3个点左右比较合适,而psi和iv则有一些固定通用的准则

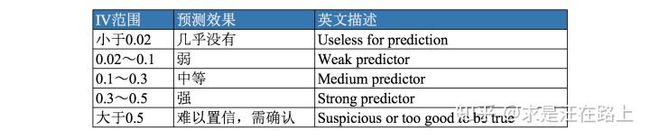
不过流程上我们还是详细的走一遍,当我们训练完模型之后,就要进行评分卡的分数转换了,需要注意的是标准逻辑回归的评分卡和gbdt这类模型的评分卡的分数转换存在着较大的差异,需要注意,我们所谈论的是银行使用的标准逻辑回归评分卡,银行的标准逻辑回归评分卡并不像我们想象的那样使用逻辑回归拟合一下,然后预测的概率结果做一个分数的映射变换就行,标准的逻辑回归评分卡一定要对所有的特征进行分箱并且做woe变换转化为woe编码的形式然后进行评分卡的转换,为了进行比较我们首先给出常规的机器学习算法的分数转换公式,然后给出标准逻辑回归评分卡的分数转换公式
clf = LogisticRegression(C=0.01,)# class_weight='balanced')
clf.fit(dev[cols],dev.bad_ind)
#LogisticRegression(C=0.01, class_weight=None, dual=False, fit_intercept=True,
# intercept_scaling=1, l1_ratio=None, max_iter=100,
# multi_class='auto', n_jobs=None, penalty='l2',
# random_state=None, solver='lbfgs', tol=0.0001, verbose=0,
# warm_start=False)
评分卡转换方法
首先介绍简单的评分卡转换方法,也是gbdt等这类机器学习模型使用的评分卡转换方法
我们将客户违约的概率表示为p,则正常的概率为1-p。因此,可以设:
Odds = p 1 − p \text { Odds }=\frac{p}{1-p} Odds =1−pp此时,客户违约的概率p可表示为:
p = O d d s 1 + O d d s p=\frac{O d d s}{1+O d d s} p=1+OddsOdds评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义,即可表示为下式: Score = A − B log ( O d d s ) \text { Score }=A-B \log (O d d s) Score =A−Blog(Odds)其中,A和B是常数。式中的负号可以使得违约概率越低,得分越高。通常情况下,这是分值的理想变动方向,即高分值代表低风险,低分值代表高风险。
式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下,需要设定两个假设:
(1)给某个特定的比率设定特定的预期分值;
(2)确定比率翻番的分数(PDO)(point of double odds)
根据以上的分析,我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P-PDO。代入式中,可以得到如下两个等式: P = A − B log ( x ) P − P D O = A − B log ( 2 x ) \begin{gathered} P=A-B \log (x) \\ P-P D O=A-B \log (2 x) \end{gathered} P=A−Blog(x)P−PDO=A−Blog(2x)例如这里的大P可以设定为600分,pdo=50分,x表示的是odds,即坏客户概率/好客户概率
假设我们期望x=(bad/good)=0.05 时的分值为50分,PDO为10分(即每增加10分 bad/good比例就会缩减一半),代入式中求得:
50=A-B*log(0.05)
50-10=A-B*log(0.1)
计算得到:
B=14.43,A=6.78, Score = 6.78 − 14.43 log ( Odds ) \text { Score }=6.78-14.43 \log (\text { Odds }) Score =6.78−14.43log( Odds )评分卡刻度参数A和B确定以后,就可以计算比率和违约概率,以及对应的分值了。
我们简单推导可以得到,
PDO=B log(2x)-B log(x)=B(log(2))
B=PDO/ln(2)
A=base_score+B * log(odds)
def calculate_A_B(prob=0.5,base_score=600,pdo=50):
odds=prob/(1-prob)
B=pdo/(np.log(2*odds)-np.log(odds))
A=base_score+B*np.log(odds)
return A,B#A-B*np.log(odds)
A,B=calculate_A_B()
A,B
#(600.0, 72.13475204444818)
def prob_to_score(prob):
return round(A-B*np.log(prob/(1-prob))) #一般我们需要得到的是整数分
这里我们假设prob=0.5,即odds=0.5/(1-0.5)=1的时候对应的base_score=600分,并且用户的分数每增加50分(pdo),则odd缩减为原来的1/2,即坏客户和好客户的比例缩小
print(str(0.01)+'->'+str(prob_to_score(0.01)))
print(str(0.1)+'->'+str(prob_to_score(0.1)))
print(str(0.2)+'->'+str(prob_to_score(0.2)))
print(str(0.3)+'->'+str(prob_to_score(0.3)))
print(str(0.4)+'->'+str(prob_to_score(0.4)))
print(str(0.5)+'->'+str(prob_to_score(0.5)))
print(str(0.6)+'->'+str(prob_to_score(0.6)))
print(str(0.7)+'->'+str(prob_to_score(0.7)))
print(str(0.8)+'->'+str(prob_to_score(0.8)))
print(str(0.9)+'->'+str(prob_to_score(0.9)))
print(str(0.99)+'->'+str(prob_to_score(0.99)))
#0.01->931.0
#0.1->758.0
#0.2->700.0
#0.3->661.0
#0.4->629.0
#0.5->600.0
#0.6->571.0
#0.7->539.0
#0.8->500.0
#0.9->442.0
#0.99->269.0
可以看到概率越高则信用评分越低,概率越低则信用评分越高
上述就是常规的评分卡概率转换分数的实现了,需要注意的是base_score,pdo以及base_score对应的概率值,我们都是主观定义为600,50,0.5的,当然不同机构有自己不同的习惯,不可一概而论
相对来说,标准的逻辑回归评分卡就比较麻烦,首先大家需要知道,标准的逻辑回归评分卡必须对所有变量进行分箱然后转化为woe编码的形式才可以
标准的逻辑回归评分卡是怎么回事?
首先回到逻辑回归的公式:
我们设 g(x)=(w1x1+w2x2+…+wnxn+w0)
则逻辑回归的输出为 sigmoid(g(x))=1/(1+np.e**(-g(x)))
注意,一般我们默认坏客户标签为1,所以这里以严谨的概率公式表示为:
P(y=1|x)=1/(1+np.e**(-g(x)))=p
则很容易可以得到:
P(y=0|x)=1-1/(1+np.e**(-g(x)))=np.e**(-g(x))/(1+np.e**(-g(x)))=1-p
我们将p/(1-p)并且取对数可以得到:
ln(p/(1-p))=1/(1+np.e**(-g(x))) / np.e**(-g(x))/(1+np.e**(-g(x)))=ln(np.e**(-g(x)))=-g(x)=-(w1x1+w2x2+…wnxn+w0)
即:
ln(p/(1-p))=ln(odds)=-(w1x1+w2x2+…wnxn+w0) 公式1
我们前面提到过,评分卡转换的公式为:
score=A-B* ln(odds)则,我们将公式1代入可以得到:
score=A-B* (w1x1+w2x2+…+wnxn+w0) 公式2
可以看到,当我们得到公式2之后,对于score的计算来说,A和B是固定的,w0 ~ wn 经过逻辑回归模型训练完之后固定下来,x1 ~ xn是样本的n个特征,则我们直接使用样本的特征xi和权重系数wi进行相乘求和之后再使用A和B这两个已知常数代入公式2计算就可以得到score了,那么当我们对特征进行woe编码之后再代入得思路是类似得,毕竟woe编码本质上也就是一个连续型特征,只不过有一个需要注意得小细节
我们前面提到过,woe的公式如下: W O E i = ln ( Bad i Bad T / Good i Good T ) = ln ( Bad i Good i ) − ln ( Bad T Good T ) W O E_{i}=\ln \left(\frac{\operatorname{Bad}_{i}}{\operatorname{Bad}_{T}} / \frac{\operatorname{Good}_{i}}{\operatorname{Good}_{T}}\right)=\ln \left(\frac{\operatorname{Bad}_{i}}{\operatorname{Good}_{i}}\right)-\ln \left(\frac{\operatorname{Bad}_{T}}{\operatorname{Good}_{T}}\right) WOEi=ln(BadTBadi/GoodTGoodi)=ln(GoodiBadi)−ln(GoodTBadT)即WOEi=ln(odds_i)-ln(odds_t) 其中WOEi表示某个变量的第i个分箱对应的woe编码值,odds_i表示的是第i个分箱对应的坏客户/好客户比例,odds_t为所有坏客户/所有好客户比例是一个常数,将WOE的公式代入公式2,我们可以得到:

这里实际上是对woe的分箱结果做了展开,什么意思呢?举个例子,假设我们有一个特征x1,其对应的权重系数w1=0.5,假设x1=【1,1,2,2.5,3,3】,本来计算的时候呢,我们是用w1 * x1,例如样本k的x1=1,则其对应的w1 * x1=0.5 * 1=0.5 ,现在我们进行了分箱,假设分成两个箱子,分箱点位2.1,则x1分箱之后变成了[1,1,1,2,2,2]并且假设我们的woe计算结果分别位0.25,0.45,则x1经过woe转换后变成了[0.25,0.25,0.25,0.45,0.45,0.45],此时,我们有两种计算方法,还是以k1为例:
- 1、k1的x1=1,落入第1个箱子,对应的woe的值为0.25,则其w1 * x1=0.5 * 0.25;
- 2、标准逻辑回归评分卡的做法,对x1的woe分箱结果进行展开变成了 1,2,则对于k1而言,x1=1落入第1个箱子,则其对应的结果为:
箱子1 箱子 2
1 0
则k1的计算结果为 w1 * 箱子1对应的woe编码值 * 1+ w1 * 箱子2对应的woe编码值 * 0
那么依次类推,我们对所有的woe分箱都做展开然后进行上述的计算就可以得到最终的score了
因此,标准逻辑回归评分卡的必做步骤:
1、分箱;
2、woe编码;
3、模型训练;
4、分数转换
这些通过toad就可以轻松实现了
from toad.scorecard import ScoreCard
card = ScoreCard(combiner=combiner,
transer=t, C=0.1,
class_weight='balanced',
base_score=600, ##
base_odds=35,
pdo=60,
rate=2)
### 这里是参数的意义实际上是假定,base_odds为35分的时候对应的base score为600分,pdo增加60分,翻番2倍
card.fit(dev[['credit_info','act_info','person_info']],dev.bad_ind)
final_card = card.export(to_frame=True)
final_card
card.predict(dev[['credit_info','act_info','person_info']])
#array([426.63952384, 126.17875494, 126.17875494, ..., 196.43707901,
# 351.62266861, 196.43707901])
这样就可以很方便的得到我们的用户评分了~
不过其实一般来说我们按照常规的分数转换规则就可以了,标准lr的麻烦的转换方法没有太大必要和意义也不具备普适性,只对lr有效
下面我们重新导入数据集,尝试使用不同的机器学习算法来进行模型的构建
# 加载数据
import toad
from toad.metrics import *
import pandas as pd
import numpy as np
import lightgbm as lgb
import xgboost as xgb
import catboost as cab
import tensorflow as tf
from sklearn.linear_model import LogisticRegression
data_all = pd.read_csv("scorecard.txt")
from toad.metrics import *
cols=list(data_all.columns)
cols.remove('bad_ind')
cols.remove('uid')
cols.remove('samp_type')
data_all[cols].isnull().sum()
#td_score 0
#jxl_score 0
#mj_score 0
#rh_score 0
#zzc_score 0
#zcx_score 0
#person_info 0
#finance_info 0
#credit_info 0
#act_info 0
#dtype: int64
注意,凡是使用广义线性回归,包括逻辑回归、svm、神经网络,都一定要对数据进行标准化转化为同一个量纲,这主要是因为梯度下降法对于不同量纲的特征其训练具有局限性,如果不同特征的量纲差距很大,则梯度下降的过程中会走 “之” 子型优化路径,导致了整个梯度下降法的过程中迭代收敛的效率非常低,甚至难以收敛,实践的经验告诉我们,量纲差异大的时候lr或者nn几乎不可收敛
from sklearn.preprocessing import StandardScaler
sd= StandardScaler()
data_all[cols]=sd.fit_transform(data_all[cols])
# 开发样本、验证样本与时间外样本
dev = data_all[(data_all['samp_type'] == 'dev')]
val = data_all[(data_all['samp_type'] == 'val') ]
off = data_all[(data_all['samp_type'] == 'off') ]
lr模型
clf = LogisticRegression(C=0.01,)# class_weight='balanced')
clf.fit(dev[cols],dev.bad_ind)
prob_dev = clf.predict_proba(dev[cols])[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
#训练集
#F1: 0.03292367010060847
#KS: 0.44285399535437714
#AUC: 0.7940500029473107
#跨时间
#F1: 0.05059384016640944
#KS: 0.4044682306848751
#AUC: 0.7662764431863981
#跨时间
#F1: 0.04024292988160236
#KS: 0.3985822108812256
#AUC: 0.7634742964832345
#模型PSI: 0.0
可以看到,这里除了标准化之外我们没有对变量进行任何处理,达到了比原来好的多的结果,但是这并不代表分箱、woe编码等这类方法无用,对于不同数据集,我们应该根据实际的模型的问题选择不同的方法进行处理,从而解决各类常见的问题例如过拟合、模型稳定性不佳等等,思维要灵活,而不要固化,建模就像搭积木一样,我们不用拘泥于搭建一个什么样的城堡,而要把经历放在积木构造的熟悉和灵活的应用上,知道什么数据场景下使用什么方法来处理是一个算法工程师的核心竞争力
gbdt模型
下面我们使用gbdt系列算法以及nn来尝试构建一个大数据模型(gbdt基本上大小数据集通吃,nn仅适用于数据量足量的数据集才会有好的效果)
clf =xgb.XGBClassifier()
clf.fit(dev[cols],dev.bad_ind)
prob_dev = clf.predict_proba(dev[cols])[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
#训练集
#F1: 0.032894043226146544
#KS: 0.5270742873203813
#AUC: 0.8448107019311604
#跨时间
#F1: 0.050476574036783455
#KS: 0.4384889072180409
#AUC: 0.7819580845619594
#跨时间
#F1: 0.04012516105282533
#KS: 0.4140934442353946
#AUC: 0.7773836876701994
#模型PSI: 0.2156405956229024
可以看到,xgb的拟合能力是要秒杀lr的,但是模型的稳定性整体比较差,主要是因为复杂的非线性模型很容易发生过拟合的问题,对于数据的变化很敏感,这部分我们可以通过调整参数来约束模型的复杂度从而降低过拟合和稳定性差的问题
clf =xgb.XGBClassifier(max_depth=3,subsample=0.8,colsample_bytree=0.8,n_estimators=100)
clf.fit(dev[cols],dev.bad_ind)
prob_dev = clf.predict_proba(dev[cols])[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
#训练集
#F1: 0.032805157247861184
#KS: 0.5295780267431727
#AUC: 0.8447893861134259
#跨时间
#F1: 0.050469798657718126
#KS: 0.4295563824502535
#AUC: 0.7836710687874329
#跨时间
#F1: 0.04024292988160236
#KS: 0.4086745374707534
#AUC: 0.7738114490894382
#模型PSI: 0.04114880159663464
可以看到,通过简单的参数调整,我们约束了模型的能力,并且在损失很少量的精度的情况下大大提高了模型的psi
这里我们也可以尝试一下lightgbm和catboost这两个框架看看效果如何
clf =lgb.LGBMClassifier(max_depth=3,subsample=0.8,colsample_bytree=0.8,n_estimators=100)
clf.fit(dev[cols],dev.bad_ind)
prob_dev = clf.predict_proba(dev[cols])[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols])[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
#训练集
#F1: 0.032894043226146544
#KS: 0.5451180272928814
#AUC: 0.8560622833945661
#跨时间
#F1: 0.050597235270433506
#KS: 0.43172826199023345
#AUC: 0.7790822093709873
#跨时间
#F1: 0.04024046129309287
#KS: 0.41308432848500526
#AUC: 0.7728870920475678
#模型PSI: 0.021290596262379426
clf =cab.CatBoostClassifier(depth=3,bagging_temperature = 0.2,iterations=100)
clf.fit(dev[cols].values,dev.bad_ind)
prob_dev = clf.predict_proba(dev[cols].values)[:,1]
print('训练集')
print('F1:', F1(prob_dev,dev.bad_ind))
print('KS:', KS(prob_dev,dev.bad_ind))
print('AUC:', AUC(prob_dev,dev.bad_ind))
prob_val = clf.predict_proba(val[cols].values)[:,1]
print('跨时间')
print('F1:', F1(prob_val,val.bad_ind))
print('KS:', KS(prob_val,val.bad_ind))
print('AUC:', AUC(prob_val,val.bad_ind))
prob_off = clf.predict_proba(off[cols].values)[:,1]
print('跨时间')
print('F1:', F1(prob_off,off.bad_ind))
print('KS:', KS(prob_off,off.bad_ind))
print('AUC:', AUC(prob_off,off.bad_ind))
print('模型PSI:',toad.metrics.PSI(prob_dev,prob_off))
#训练集
#F1: 0.03262834417932032
#KS: 0.5130663326732602
#AUC: 0.8337584646843421
#跨时间
#F1: 0.050597235270433506
#KS: 0.45442764619321213
#AUC: 0.7824088254866859
#跨时间
#F1: 0.04025280726514082
#KS: 0.41395490758767756
#AUC: 0.7771723754417196
#模型PSI: 0.010263047181651571