深度学习 LSTM长短期记忆网络原理与Pytorch手写数字识别
深度学习 LSTM长短期记忆网络原理与Pytorch手写数字识别
- 一、前言
- 二、网络结构
- 三、可解释性
- 四、记忆主线
- 五、遗忘门
- 六、输入门
- 七、输出门
- 八、手写数字识别实战
-
- 8.1 引入依赖库
- 8.2 加载数据
- 8.3 迭代训练
- 8.4 数据验证
- 九、参考资料
一、前言
基本的RNN存在梯度消失和梯度爆炸问题,会忘记它在较长序列中以前看到的内容,只具有短时记忆。得到比较广泛应用的是LSTM(Long Short Term Memory)——长短期记忆网络,它在一定程度上解决了这两个问题。
二、网络结构
我们来看一下LSTM网络的结构图:
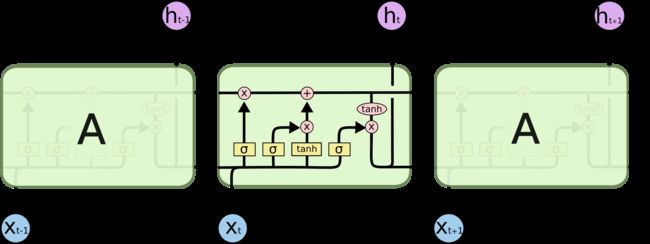
咱们放大看看,由于网上找不到清晰版的示例图,亲绘了一幅:

LSTM包含遗忘门、输入门、输出门。分别用于LSTM的三个步骤:旧记忆的遗忘、新记忆的输入、最终结果的输出。
三、可解释性
为什么要这么设计LSTM网络呢?我们打个比方:
小明上次考了数学,留下的大部分是数学的知识记忆 C t − 1 C_{t-1} Ct−1;这次考生物,一些数学知识用不到,部分复杂的公式自然而然地被遗忘了 f t ⊙ C t − 1 f_t\odot{C}_{t-1} ft⊙Ct−1;复习生物知识一本书 C ~ t \tilde{C}_t C~t,大概记得八成 i t ⊙ C ~ t i_t\odot\tilde{C}_t it⊙C~t,那么当前的记忆 C t = f t ⊙ C t − 1 + i t ⊙ C ~ t C_t=f_t\odot{C}_{t-1}+i_t\odot\tilde{C}_t Ct=ft⊙Ct−1+it⊙C~t;考试时,成绩受到考题和当前记忆 C t C_t Ct的影响 h t = O t ⊙ tanh C t h_t=O_t\odot\tanh{C_t} ht=Ot⊙tanhCt。
注: ⊙ \odot ⊙是矩阵的点乘符号,即两个矩阵对应元素相乘
四、记忆主线
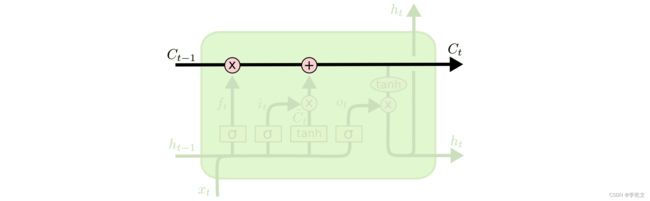
如上图所示,原有记忆是 C t − 1 C_{t-1} Ct−1,经过遗忘(用矩阵参数进行点乘)、添加新记忆(加上新的记忆矩阵),当前最新的记忆就变成了 C t C_{t} Ct,如此循环,不重要的记忆就会忘记、重要的记忆就会一直流传下去。
五、遗忘门
第一步,我们会遗忘部分原有的记忆。
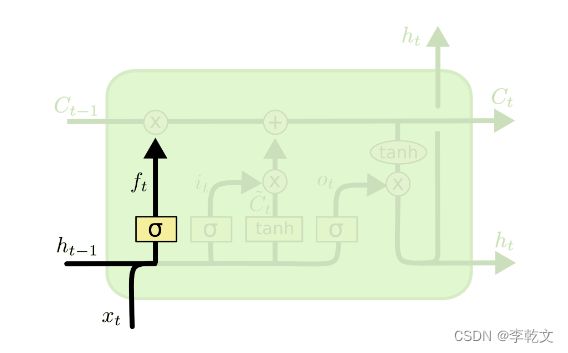
如上图所示, f t = σ ( W x f x t + W h f h t − 1 + b f ) f_t=\sigma(W_{xf}x_t+W_{hf} h_{t-1}+b_f) ft=σ(Wxfxt+Whfht−1+bf)
σ \sigma σ代表sigmoid函数。原有记忆是 C t − 1 C_{t-1} Ct−1,遗忘后为 f t ⊙ C t − 1 f_t\odot{C}_{t-1} ft⊙Ct−1
六、输入门
第二步,我们会新增部分新的记忆。我们要确定,哪些新信息要保留到记忆细胞里。

如上图所示,
C ~ t = t a n h ( W x c x t + W h c h t − 1 + b c ) i t = σ ( W x i x t + W h i h t − 1 + b i ) \begin{aligned} \tilde{C}_t&=tanh(W_{xc}x_t+W_{hc}h_{t-1} +b_c)\\ i_t&=\sigma(W_{xi}x_t+W_{hi} h_{t-1}+b_i) \end{aligned} C~tit=tanh(Wxcxt+Whcht−1+bc)=σ(Wxixt+Whiht−1+bi)
C ~ t \tilde{C}_t C~t表示所有的输入信息,但我们不是所有的都记得, i t i_t it控制记忆程度, i t ⊙ C ~ t i_t\odot\tilde{C}_t it⊙C~t是本次输入所记住的信息。
遗忘后的记忆是 f t ⊙ C t − 1 f_t\odot{C}_{t-1} ft⊙Ct−1,输入新的记忆后, C t = f t ⊙ C t − 1 + i t ⊙ C ~ t C_t=f_t\odot{C}_{t-1}+i_t\odot\tilde{C}_t Ct=ft⊙Ct−1+it⊙C~t
七、输出门
第三步,我们要根据现有记忆 C t C_t Ct,输出我们需要的内容。

如上图所示,
O t = σ ( W x o x t + W h o h t − 1 + b o ) h t = O t ⊙ tanh ( C t ) \begin{aligned} O_t&=\sigma(W_{xo}x_t+W_{ho} h_{t-1}+b_o)\\ h_t&=O_t\odot\tanh(C_t) \end{aligned} Otht=σ(Wxoxt+Whoht−1+bo)=Ot⊙tanh(Ct)
这就是LSTM网络的思想原理,接下来我们将用于手写数字识别实战。
八、手写数字识别实战
8.1 引入依赖库
import torch
import torch.nn as nn
from torchvision import datasets,transforms
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
8.2 加载数据
train_data = datasets.MNIST(root="./data",train=True,transform=transforms.ToTensor(),download=False)
batch_size=64
train_loader = DataLoader(train_data,batch_size=batch_size,shuffle=True)
test_data = datasets.MNIST(root="./data",train=False,transform=transforms.ToTensor(),download=False)
test_x = test_data.data.type(torch.FloatTensor)[:2000]/255. #取2000个样本数据并将其缩放为0~1范围
test_y = test_data.targets[:2000]
print(train_data.data.shape)
torch.Size([60000, 28, 28])
8.3 迭代训练
#迭代次数
epochs=1
#学习率
learning_rate=0.01
plt_epoch=[]
plt_loss=[]
class MyModel(nn.Module):
def __init__(self):
super().__init__()
self.rnn = nn.LSTM( # LSTM 效果要比 nn.RNN() 好多了
input_size=28, # 图片每行的数据像素点
hidden_size=64, # rnn hidden unit
num_layers=1, # 有几层 RNN layers
batch_first=True, # input & output 会是以 batch size 为第一维度的特征集 e.g. (batch, time_step, input_size)
)
self.out = nn.Linear(64, 10) # 输出层
def forward(self, x):
# x shape (batch, time_step, input_size)
# r_out shape (batch, time_step, output_size)
# h_n shape (n_layers, batch, hidden_size) LSTM 有两个 hidden states, h_n 是分线, h_c 是主线
# h_c shape (n_layers, batch, hidden_size)
r_out, (h_n, h_c) = self.rnn(x, None) # None 表示 hidden state 会用全0的 state
# 选取最后一个时间点的 r_out 输出
# 这里 r_out[:, -1, :] 的值也是 h_n 的值
out = self.out(r_out[:, -1, :])
return out
model = MyModel()
#损失函数
cost=nn.CrossEntropyLoss()
#迭代优化器
optmizer=torch.optim.Adam(model.parameters(),lr=learning_rate)
for epoch in range(epochs):
for step, (images, labels) in enumerate(train_loader):
images=images.view(-1,28,28)
#预测结果
output=model(images) #调用__call__函数
#计算损失值
loss=cost(output,labels)
#在反向传播前先把梯度清零
optmizer.zero_grad()
#反向传播,计算各参数对于损失loss的梯度
loss.backward()
#根据刚刚反向传播得到的梯度更新模型参数
optmizer.step()
plt_epoch.append(step+1)
plt_loss.append(loss.item())
#打印损失值
if step % 50 == 0:
pred_y = model(test_x)
pred_y=pred_y.argmax(dim=1) #返回最大值的下标
print(f"step:{step},loss:{loss.item():.4f},accuracy: {(torch.sum(pred_y == test_y)/test_y.size()[0]) * 100:.2f}%")
# 保存模型
torch.save(model, 'LSTM_Digits.pt')
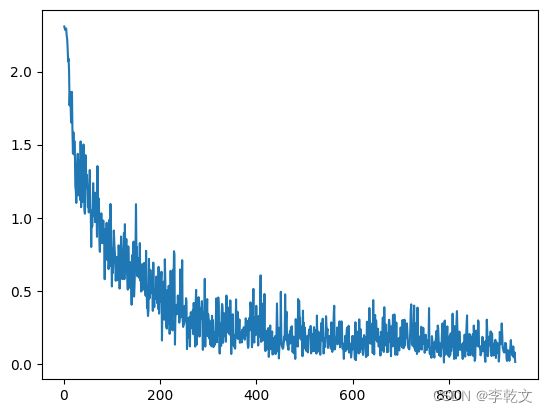
#绘制迭代次数与损失函数的关系
plt.plot(plt_epoch,plt_loss)
step:0,loss:2.3081,accuracy: 8.75%
step:50,loss:1.0913,accuracy: 59.40%
step:100,loss:0.7879,accuracy: 70.30%
step:150,loss:0.7618,accuracy: 73.75%
step:200,loss:0.4271,accuracy: 86.70%
step:250,loss:0.3963,accuracy: 90.65%
step:300,loss:0.2965,accuracy: 91.85%
step:350,loss:0.3396,accuracy: 94.15%
step:400,loss:0.2283,accuracy: 92.30%
step:450,loss:0.4932,accuracy: 94.05%
step:500,loss:0.2487,accuracy: 93.25%
step:550,loss:0.1460,accuracy: 94.20%
step:600,loss:0.1908,accuracy: 94.70%
step:650,loss:0.1521,accuracy: 92.35%
step:700,loss:0.1530,accuracy: 94.80%
step:750,loss:0.1192,accuracy: 94.65%
step:800,loss:0.0478,accuracy: 95.30%
step:850,loss:0.0535,accuracy: 95.70%
step:900,loss:0.1174,accuracy: 95.45%
8.4 数据验证
#加载模型
model=torch.load('LSTM_Digits.pt')
#预测结果
pred_y=model(test_x)
#计算损失值
loss=cost(pred_y,test_y)
print('loss:',loss.detach().item())
pred_y=pred_y.argmax(dim=1) #返回最大值的下标
print(f"准确率: {(torch.sum(pred_y == test_y)/test_y.size()[0]) * 100}%")
# 打印10个预测结果
pred_y = model(test_x[:10].view(-1, 28, 28))
pred_y=pred_y.argmax(dim=1) #返回最大值的下标
print('预测数字',pred_y)
print( '真实数字',test_y[:10])
loss: 0.11265470087528229
准确率: 96.45000457763672%
预测数字 tensor([7, 2, 1, 0, 4, 1, 4, 9, 5, 9])
真实数字 tensor([7, 2, 1, 0, 4, 1, 4, 9, 5, 9])
九、参考资料
《如何从RNN起步,一步一步通俗理解LSTM》
《大白话讲解LSTM长短期记忆网络 如何缓解梯度消失,手把手公式推导反向传播》
《Understanding LSTM Networks》
《【Pytorch教程】:RNN 循环神经网络 (分类)》