《动手学》-BN层,BN与LN区别
目录
- 1.理论
-
- 1.1 问题引出
- 1.2 基本定义
- 1.3作用
- 1.4 总结
- 2.代码
- 3. QA
1.理论
1.1 问题引出
批量归一化
底部就是靠近输入那一层
正向forward算出损失来,通过反向得到梯度,根据链式法则,梯度相乘,越靠近底部的变量梯度越小,导致底部层训练的慢。

1.2 基本定义
根据之前提到的将各个层的分布(均值和方差)固定,可以很大层度上将各个层的梯度固定在一个很合理的值。通过小批量的减均值除方差,将分布固定在0,1分布上。然后通过γ和β两个可学习的参数小幅移动分布。


1.3作用
1.4 总结
2.代码
X.mean(dim=0)在特征维上进行批量归一化
X.mean(dim=(0, 2, 3), keepdim=True):在通道维度上进行批量归一化
import torch
from torch import nn
from d2l import torch as d2l
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过 `is_grad_enabled` 来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean)**2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean)**2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.data
class BatchNorm(nn.Module):
# `num_features`:完全连接层的输出数量或卷积层的输出通道数。
# `num_dims`:2表示完全连接层,4表示卷积层
def __init__(self, num_features, num_dims):
super().__init__()
if num_dims == 2:
shape = (1, num_features)
else:
shape = (1, num_features, 1, 1)
# 参与求梯度和迭代的拉伸和偏移参数,分别初始化成1和0
self.gamma = nn.Parameter(torch.ones(shape))
self.beta = nn.Parameter(torch.zeros(shape))
# 非模型参数的变量初始化为0和1
self.moving_mean = torch.zeros(shape)
self.moving_var = torch.ones(shape)
def forward(self, X):
# 如果 `X` 不在内存上,将 `moving_mean` 和 `moving_var`
# 复制到 `X` 所在显存上
if self.moving_mean.device != X.device:
self.moving_mean = self.moving_mean.to(X.device)
self.moving_var = self.moving_var.to(X.device)
# 保存更新过的 `moving_mean` 和 `moving_var`
Y, self.moving_mean, self.moving_var = batch_norm(
X, self.gamma, self.beta, self.moving_mean, self.moving_var,
eps=1e-5, momentum=0.9)
return Y
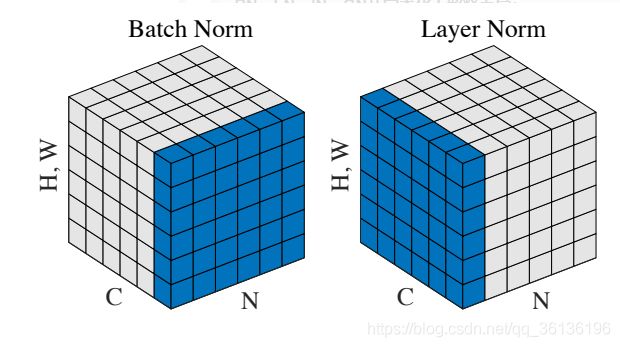
将输入的图像shape记为[N, C, H, W],这几个方法主要的区别就是在,
batchNorm是在batch上,对NHW做归一化,对小batchsize效果不好,dim=(0, 2, 3);
layerNorm在通道方向上,对CHW归一化,主要对RNN作用明显;dim=(1, 2, 3);
net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4),
nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16,
kernel_size=5), BatchNorm(16, num_dims=4),
nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(), nn.Linear(16 * 4 * 4, 120),
BatchNorm(120, num_dims=2), nn.Sigmoid(),
nn.Linear(120, 84), BatchNorm(84, num_dims=2),
nn.Sigmoid(), nn.Linear(84, 10))
lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
看从第一个批量归一化层中学到的拉伸参数 gamma 和偏移参数 beta
net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))
简明实现
net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6),
nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16),
nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(), nn.Linear(256, 120), nn.BatchNorm1d(120),
nn.Sigmoid(), nn.Linear(120, 84), nn.BatchNorm1d(84),
nn.Sigmoid(), nn.Linear(84, 10))
3. QA
- Xavier是作用在初始化阶段的,BN是作用在整层的
- 一般先根据显存利用率调batch_size,然后调节学习率,epoch可以选大一点,中途可以停掉的
- bn是(mlp)特征维度,(cnn)通道维度做normalization,LN是样本内做normalization
每秒处理的样本数,example/s

