论文阅读笔记《Robust Point Matching via Vector Field Consensus》
核心思想
本文提出一种基于向量场一致性的(Vector Field Consensus)非刚性(non-rigid)匹配方法(VFC)。所谓刚性(rigid)的匹配方法通常是使用参数化模型(如单应性矩阵、对极几何)来准确描述匹配点之间的对应关系的,如RANSAC方法,而非刚性匹配方法则是使用类似于能量函数的方法来描述匹配点之间的匹配程度,而无法得到准确的几何关系。作者提出使用向量场(Vector Field)来描述特征点之间的匹配关系,向量场中的每个向量都是由原图中的特征点的位置指向待匹配图像中对应匹配点的位置,也就是描述出了匹配点的位移情况(类似于光流?),如下图所示

图(a)表示了两幅图像之间的匹配关系,蓝色表示正确匹配,红色表示误匹配,图(b)是所有匹配点对应的位移向量,图(d)是由图(b)经过插值得到向量场,而图©则是只有正确匹配点对应的位移向量,图(e)是图©经过插值得到向量场。很显然,仅有正确匹配点对应的向量场直观上看起来更加的一致、平滑、有规律,而带有误匹配点的向量场则显得杂乱无章。正是利用这样一个先验知识,作者提出了基于向量场一致性的匹配方法。
作者首先介绍了如何从一个包含离群点(误匹配点)的向量场通过迭代优化的方式,剔除离群点,并获得最优的向量场。刚才说到向量场是由一堆描述匹配点之间位移的向量构成的,这只是针对于图像匹配任务而言的,从更一般、更抽象的角度上来说,对于由若干输入-输出对构成的集合 S = { ( x n , y n ) ∈ X × Y : n ∈ N } S=\{(x_n, y_n)\in\mathcal{X}\times\mathcal{Y}:n\in N\} S={(xn,yn)∈X×Y:n∈N}, x n x_n xn表示输入, y n y_n yn表示输出,且 y n = f ( x n ) y_n=\mathbf{f}(x_n) yn=f(xn), f \mathbf{f} f就是构成向量场的向量。但是满足这样一种映射关系的向量 f \mathbf{f} f有无数种可能,所以必须引入一种正则化约束,使其获得有倾向性偏好的最优结果。我们引入的倾向性偏好就是上文提到的“平滑性”,我们希望找到一个向量场,使其平滑性够高,这在图像匹配任务中也就意味着正确匹配点更多,误匹配点越少。
目标已经明确了,下面就是如何实现这个目的了。作者引入了定义在再生核希尔伯特空间 H \mathcal{H} H(RKHS)内的Tikhonov正则化方法,再生核希尔伯特空间有一个特性就是可以用一个特定核函数 Γ \Gamma Γ来计算两个函数(函数可以看作是无穷维的向量)之间的内积,关于再生核希尔伯特空间的介绍建议看这篇文章https://zhuanlan.zhihu.com/p/29527729。引入Tikhonov正则化约束的目标函数如下式
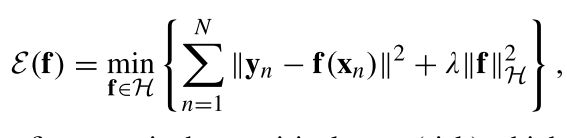
目标函数中第一项就是经验误差项,很好理解就是希望 f \mathbf{f} f映射的结果和真实的输出 y n y_n yn之间尽可能地相似,第二项就是正则化项,使用再生核希尔伯特空间 H \mathcal{H} H中的范数来描述平滑性,范数越小,说明描述该向量场需要的基向量的数量越少,表示对应向量场的平滑性、一致性越高。举个极限的例子,假设只需要一个基向量就能够描述一个向量场,那么这个向量场中的所有向量都是指向相同方向的,只不过有长度的差别,那说明一致性非常高。根据表示定理(representer theorem), f \mathbf{f} f的最优解具备以下形式

其中系数 c n c_n cn是由下式决定的

其中 Γ ~ \widetilde{\Gamma} Γ 表示 N × N N\times N N×N的块矩阵,其中第 ( i , j ) (i,j) (i,j)个块是核函数 Γ ( x i , x j ) \Gamma(x_i,x_j) Γ(xi,xj), I I I表示单位阵, Y ~ = ( y 1 T , . . . y n T ) T \widetilde{Y}=(y_1^T,...y_n^T)^T Y =(y1T,...ynT)T是由输出构成的列向量。
上述过程还存在一个问题,就是在计算过程中是将集合 S S S中的所有输入输出都用于向量场 f \mathbf{f} f优化计算了,但其中还包含很多的离群点,也就是错误的点,因此必须把他们筛选出来。作者提出一种通过最大化后验概率的方法来去除离群点,具体来说,作者假设所有的正确匹配点都符合均值为0,标准差为 σ \sigma σ的高斯分布,而离群点则满足均匀随机分布,则混合模型的概率密度函数可表示为
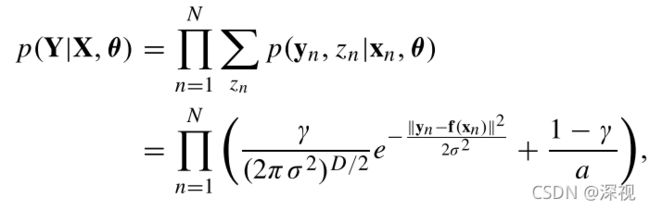
其中 z n = 1 z_n=1 zn=1表示是正确匹配点, z n = 0 z_n=0 zn=0表示离群点, γ \gamma γ表示 z n = 1 z_n=1 zn=1的概率, θ = { f , σ 2 , γ } \theta=\{\mathbf{f},\sigma^2,\gamma\} θ={f,σ2,γ}表示未知参数集合,也是我们要优化的对象。为了得到最优参数 θ ∗ \theta^* θ∗首先要引入一个先验约束,向量场 f \mathbf{f} f满足缓慢平滑运动模型,即 f \mathbf{f} f的概率分布 p ( f ) p(\mathbf{f}) p(f)满足下式

而优化的目标就是最大化后验概率密度函数
![]()
这等价于最小能量函数
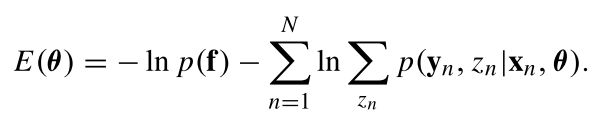
作者采用EM算法求解上式,首先得到负对数后验函数

E步骤就是使用当前的参数 θ o l d \theta^{old} θold来估计隐参数 z n z_n zn的后验分布,即 p n = P ( z n = 1 ∣ x n , y n , θ o l d ) p_n=P(z_n=1|x_n,y_n,\theta^{old}) pn=P(zn=1∣xn,yn,θold),根据贝叶斯法则计算方法为
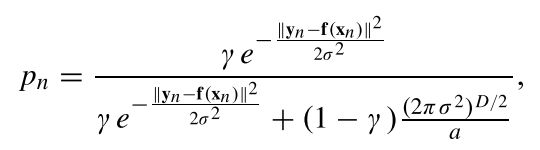
p n p_n pn描述了第 n n n个样本满足向量场 f \mathbf{f} f的程度,简单来说 p n p_n pn越大,其越有可能是正确的匹配点。
M步骤则得到修正后的参数估计 θ n e w = a r g m a x θ Q ( θ , θ o l d ) \theta^{new}=argmax_{\theta}\mathcal{Q}(\theta,\theta^{old}) θnew=argmaxθQ(θ,θold),更新过程如下

其中 V ~ = ( f ( x 1 ) T , . . . , f ( x N ) T ) T \widetilde{V}=(\mathbf{f}(x_1)^T,...,\mathbf{f}(x_N)^T)^T V =(f(x1)T,...,f(xN)T)T, P ~ = P ⊗ I \widetilde{\mathbf{P}}=\mathbf{P}\otimes \mathbf{I} P =P⊗I, P = d i a g ( p 1 , . . . , p N ) \mathbf{P}=diag(p_1,...,p_N) P=diag(p1,...,pN), ⊗ \otimes ⊗表示Kronecker内积。而向量场 f \mathbf{f} f的更新方法如下
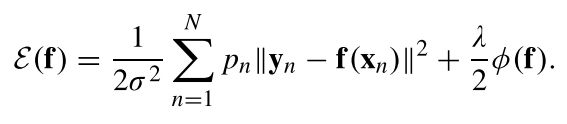
这是上面提到的优化目标函数的一个特殊形式,其中最优解 f \mathbf{f} f具有以下形式
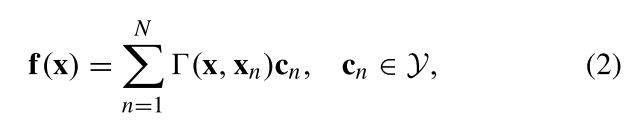
而系数 c n c_n cn由下式计算得到
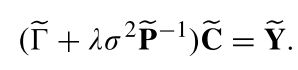
反复迭代上述E、M步骤,直到 Q \mathcal{Q} Q收敛,就能得到最优的向量场 f \mathbf{f} f,而正确匹配点集 I \mathcal{I} I,可以通过设定一个阈值 τ \tau τ,如果 p n p_n pn大于阈值则认为是正确匹配点,即

上述过程就是VFC方法的核心部分,但是在匹配过程中如果对所有的 N N N个特征点都进行上述计算过程,其时间复杂度为 o ( N 3 ) o(N^3) o(N3),这对于大规模特征点匹配显然是无法接受的,因此作者由提出了稀疏VFC方法,简单来说就是采用稀疏近似的方法来计算一个次优的向量场 f \mathbf{f} f。在每次迭代过程中都随机选择 M < < N M<

U ~ \widetilde{U} U 为 N × M N\times M N×M的块矩阵,第 ( i , j ) (i,j) (i,j)块的元素为 Γ ~ ( x i , x ~ j ) \widetilde{\Gamma}(x_i,\tilde{x}_j) Γ (xi,x~j)。
下面介绍如何将VFC方法运用到图像匹配过程中,首先还是用SIFT等方法得到一组候选的匹配点,候选集由一对匹配点的坐标构成 ( u n , v n ) (u_n,v_n) (un,vn), u n u_n un表示原图特征点的坐标, v n v_n vn表示待匹配图像特征点的坐标,对其进行归一化处理 ( u ^ n , v ^ n ) (\hat{u}_n,\hat{v}_n) (u^n,v^n),然后经过一个简单变化得到运动场的形式 x n = u ^ n x_n=\hat{u}_n xn=u^n, y n = v ^ n − u ^ n y_n=\hat{v}_n-\hat{u}_n yn=v^n−u^n。核函数选择高斯核函数,如下式
![]()
然后按照上面介绍的VFC过程,通过求解最优的向量场,就可以选择出正确匹配点了。本文介绍的方法虽然是非刚性的匹配方法,但他同样可以扩展到刚性匹配方法中,这里就不再展开介绍了。
创新点
- 将图像匹配问题转化为向量场一致性的优化问题
- 采用最大后验估计方法来求解最优的向量场,并筛选出正确匹配点
算法评价
本文提出的方法还是比较硬核的,利用正确匹配点的向量场更加一致、更加光滑这一先验约束,将寻找正确匹配点的过程转化成了向量场一致性的优化问题。由通过将正确匹配点和误匹配点定义成不同的概率分布形式,通过最大后验估计的方式计算得到最优的向量场。文中涉及了许多泛函、核函数、概率学相关的知识,本博客也只是浅显的介绍一下算法过程,为了方便理解可以阅读一下作者做的一个中文PPT报告https://wenku.baidu.com/view/3283d258f4335a8102d276a20029bd64783e62ba.html
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。