机器学习系列 11：支持向量机 03 - 非线性支持向量机

---

针对 “支持向量机” 将分为以下几个部分进行介绍：

1. 支持向量机 01 - 线性可分支持向量机和线性支持向量机
2. 支持向量机 02 - SMO（序列最小化）
3. 支持向量机 03 - 非线性支持向量机（本篇）
4. 支持向量机 04 - SVR（支持向量回归）

---

  本内容将介绍 非线性支持向量机。

一、非线性分类问题

  在 支持向量机 01 - 线性可分支持向量机和线性支持向量机 中讲解的都是线性分类问题。但是，在现实问题中存在着非线性分类问题，即在原始样本空间内并不存在一个能正确划分两类样本的超平面。

  我们先看一个例子：如图-1 所示，图中 “●” 表示正实例点，“×” 表示负实例点。可以看到，无法用一条直线（线性模型）将正负实例正确分开，但可以用一条椭圆曲线（非线性模型）将它们正确分开。

图-1 非线性分类问题

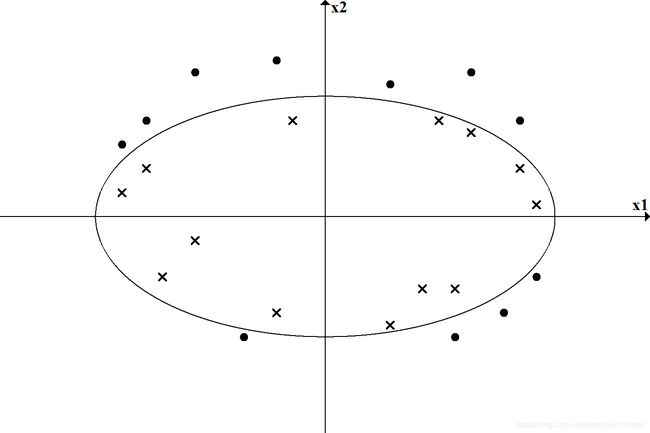
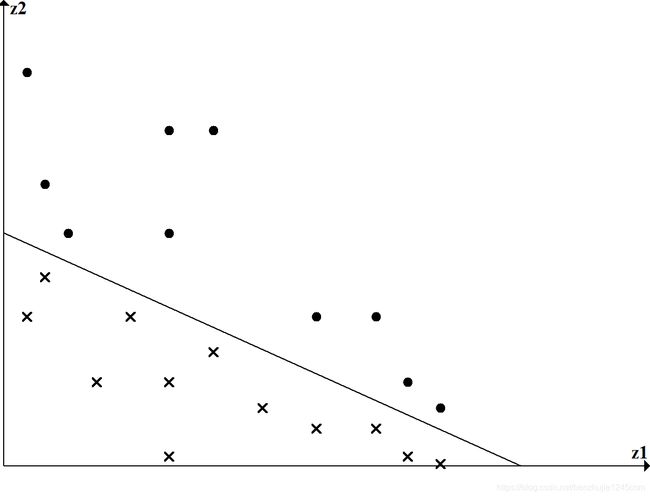
  非线性问题往往不好求解，所以希望能用解线性分类问题的方法解决这个问题。所采取的方法是进行一个非线性变换，将非线性问题变换为线性问题，通过解变换后的线性问题的方法求解原来的非线性问题。对图-1 所示的例子，通过变换，将左图中椭圆变换成右图中的直线，将非线性分类问题变换为线性分类问题。

  设原空间为 $\mathcal{X}\subseteq {\mathbb{R}}^2$，$\mathbf{x}=(x_1;x_2)\in \mathcal{X}$，新空间为 $\mathcal{Z}\subseteq {\mathbb{R}}^2$，$\mathbf{z}=(z_1;z_2)\in \mathcal{Z}$，定义从原空间到新空间的变换：

$$\mathbf{z}=\varphi (\mathbf{x})=\left((x_1{)}^2;(x_2{)}^2\right)\text{\hspace{1em}(1)}$$

经过变换 $\mathbf{z}=\varphi (\mathbf{x})$，原空间 $\mathcal{X}\subseteq {\mathbb{R}}^2$ 变换为新空间 $\mathcal{Z}\subseteq {\mathbb{R}}^2$，原空间中的点相应地变换为新空间的点，原空间的椭圆

$$w_1(x_1{)}^2+w_2(x_2{)}^2+b=0\text{\hspace{1em}(2)}$$

变换为新空间中的直线

$$w_1{z}_1+w_2{z}_2+b=0\text{\hspace{1em}(3)}$$

在变换后的新空间中，直线 $w_1{z}_1+w_2{z}_2+b=0$ 可以将变换后的正负实例点正确分开。这样，原空间的非线性可分问题就变成了新空间中的线性可分问题。

  上面的例子说明，用线性分类方法求解非线性分类问题分为两步：

• 首先，使用一个变换将原空间的数据映射到新空间。
• 然后，在新空间里用线性分类学习方法从训练数据中学习分类模型。

  核技巧 就属于这样的方法。

二、核技巧

  核技巧应用到支持向量机，其基本想法就是通过一个非线性变换将输入空间（欧式空间 ${\mathbb{R}}^n$ 或离散集合）对应于一个特征空间（希尔伯特空间 $\mathcal{H}$），使得在输入空间 ${\mathbb{R}}^n$ 中的超曲面模型对应于特征空间 $\mathcal{H}$ 中的超平面模型（支持向量机）。这样，分类问题的学习任务通过在特征空间中求解线性支持向量机就可以完成。

2.1 核函数的定义

  定义：设 $\mathcal{X}$ 是输入空间（欧式空间 ${\mathbb{R}}^n$ 或离散集合），又设 $\mathcal{H}$ 为特征空间（希尔伯特空间），存在一个从 $\mathcal{X}$ 到 $\mathcal{H}$ 的映射 $\varphi (\mathbf{x}):\mathcal{X}\to \mathcal{H}$，对所有 ${\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\in \mathcal{X}$，函数 $K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)$ 满足条件

$$K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)=\varphi \left({\mathbf{x}}^{(i)}\right)\cdot \varphi \left({\mathbf{x}}^{(j)}\right)\text{\hspace{1em}(4)}$$

则称 $K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)$ 为 核函数，式中 $\varphi \left({\mathbf{x}}^{(i)}\right)\cdot \varphi \left({\mathbf{x}}^{(j)}\right)$ 为 $\varphi \left({\mathbf{x}}^{(i)}\right)$ 与 $\varphi \left({\mathbf{x}}^{(j)}\right)$ 的內积（点积）。

  核技巧的想法是，在学习与预测中只定义核函数 $K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})$，而不是显式地定义映射函数 $\varphi$。通常，直接计算 $K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})$ 比较容易，而通过 $\varphi ({\mathbf{x}}^{(i)})$ 和 $\varphi ({\mathbf{x}}^{(j)})$ 计算 $K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})$ 并不容易。注意，$\varphi$ 是输入空间 ${\mathbb{R}}^n$ 到特征空间 $\mathcal{H}$ 的映射，特征空间 $\mathcal{H}$ 一般是高维的，甚至是无穷维的。

2.2 在支持向量机中应用核技巧

  我们注意到在线性支持向量机的对偶问题的目标函数涉及输入实例与实例之间的內积。在对偶问题的目标函数中的內积 ${\mathbf{x}}^{(i)}\cdot {\mathbf{x}}^{(j)}$ 可以用核函数 $K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})=\varphi ({\mathbf{x}}^{(i)})\cdot \varphi ({\mathbf{x}}^{(j)})$ 来代替。此时对偶问题的目标函数成为

$$\underset{\alpha }{\max }\left(\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})\right)\text{\hspace{1em}(5)}$$

求解后即可得到

$$f(\mathbf{x})=\sum _{i=1}^m{\alpha }_i{y}^{(i)}K({\mathbf{x}}^{(i)},\mathbf{x})+b\text{\hspace{1em}(6)}$$

  这等价于经过映射函数 $\varphi$ 将原来的输入空间变换为一个新的特征空间，将输入空间中的內积 ${\mathbf{x}}^{(i)}\cdot {\mathbf{x}}^{(j)}$ 变换为特征空间中的內积 $\varphi ({\mathbf{x}}^{(i)})\cdot \varphi ({\mathbf{x}}^{(j)})$，在新的特征空间里从训练样本中学习线性支持向量机。当映射函数是非线性函数时，学习到的含有核函数的支持向量机是非线性分类模型。

  也就是说，在核函数 $K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})$ 给定的条件下，可以利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在特征空间进行的，不需要显示地定义特征空间和映射函数。这样的技巧称为核技巧，它是巧妙地利用线性分类学习方法与核函数解决非线性问题的技术。在实际应用中，往往依赖领域知识直接选择核函数，核函数选择的有效性需要通过实验验证。

三、正定核

  到底什么样的函数才可当做核函数呢？通常所说的核函数实际上就是正定核函数。那我们来了解一下什么是正定核函数。

  定义：设 $\mathcal{X}\subseteq {\mathbb{R}}^2$，$K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})$ 是定义在 $\mathcal{X}\times \mathcal{X}$ 上的对称函数，如果对任意 ${\mathbf{x}}^{(i)}\in \mathcal{X}$，$i=1,2,\cdots ,m$，$K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)$ 对应的 Gram 矩阵

$$K={\left[K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)\right]}_{m\times m}\text{\hspace{1em}(7)}$$

是半正定矩阵，则称 $K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)$ 是 正定核函数。

  虽然我们已经知道了正定核函数的定义，但是对于一个具体函数 $K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)$ 来说，检验它是否为正定核函数并不容易。所以在实际问题中往往应用已有的核函数。

四、常用核函数

  以下为几种常用核函数：

名称	表达式	说明
线性核（Linear Kernel）	$K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})={\mathbf{x}}^{(i)}\cdot {\mathbf{x}}^{(j)}$	实际上就是线性 SVM。
多项式核（Polynomial Kernel）	$K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})={\left(\gamma {\mathbf{x}}^{(i)}\cdot {\mathbf{x}}^{(j)}+r\right)}^d$	斜率 $\gamma$，常数项 $r$，和多项式次数 $d\ge 1$。
高斯核（Gaussian Kernel）	$K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})=\exp \left(-\frac{\Vert \Vert {\mathbf{x}}^{(i)}-{\mathbf{x}}^{(j)}\Vert {\Vert }^2}{2{\sigma }^2}\right)$	也称为径向基核函数，libsvm 库将它作为默认核函数。 $\sigma >0$ 是高斯核的带宽。
拉普拉斯核	$K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})=\exp \left(-\frac{\Vert \Vert {\mathbf{x}}^{(i)}-{\mathbf{x}}^{(j)}\Vert \Vert }{\sigma }\right)$	$\sigma >0$
Sigmoid 核（Sigmoid Kenel）	$K({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})=\tanh (\beta {\mathbf{x}}^{(i)}\cdot {\mathbf{x}}^{(j)}+\theta )$	$\tanh$ 为双曲正切函数，$\beta >0$，$\theta <0$。

  此外，还可以通过函数组合得到核函数，例如：

• 若 $K_1$ 和 $K_2$ 为核函数，则对于任意正数 ${\gamma }_1$ 和 ${\gamma }_2$，其线性组合 ${\gamma }_1{K}_1+{\gamma }_2{K}_2$ 也是核函数。

• 若 $K_1$ 和 $K_2$ 为核函数，则核函数的直积 $K_1⨂K_2({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})=K_1({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})K_2({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)})$ 也是核函数。

• 若 $K_1$ 为核函数，则对于任意函数 $g(\mathbf{x})$，$K\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)=g\left({\mathbf{x}}^{(i)}\right)K_1\left({\mathbf{x}}^{(i)},{\mathbf{x}}^{(j)}\right)g\left({\mathbf{x}}^{(j)}\right)$ 也是核函数。

五、总结

  求取非线性支持向量机的方法与线性支持向量机一样，不同的是：将线性支持向量机中的 內积 替换成 核函数。在实际问题中往往使用已有的核函数（例如，高斯核函数、多项式核函数等等）。

参考：
[1] 周志华《机器学习》
[2] 李航《统计学习方法》
[3] https://zhuanlan.zhihu.com/p/29872905
[4] https://www.cnblogs.com/pinard/p/6103615.html