支持向量机总结
SVM算法总结
SVM的原理是什么?
支持向量机(Support Vecor Machine,SVM)是既可以解决线性问题又可以解决非线性问题,既可以用于分类,又可以用于回归的经典算法。它的基本模型是在特征空间中寻找间隔最大化的分离超平面,使距离最近的样本点到该超平面的距离尽可能的远。(间隔最大使它有别于感知机)
- 当训练样本线性可分时,通过硬间隔最大化,学习一个线性分类器,即Hard-Margin SVM;
- 当训练数据近似线性可分时,引入松弛变量,通过软间隔最大化,学习一个线性分类器,即Soft-Margin SVM;
- 当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
SVM为什么采用间隔最大化?
- 当训练数据线性可分时,存在无穷个分离超平面可以将两类数据正确分开。感知机利用误分类最小策略,求得分离超平面,不过此时的解有无穷多个。SVM利用间隔最大化求得最优分离超平面,解是唯一的。
- 间隔最大化的超平面所产生的分类结果鲁棒性最好,对未知样本的泛化能力最强。
为什么要将求解SVM的原始问题转换为其对偶问题?
- 对偶问题往往更易求解。寻找约束存在时的最优点的时候,约束的存在虽然减小了需要搜寻的范围,但是却使问题变得更加复杂。为了使问题变得易于处理,把目标函数和约束全部融入一个新的函数,即拉格朗日函数,再通过这个函数来寻找最优点。
- 对偶问题将原始问题中的约束转为了对偶问题中的等式约束
- 方便核函数的引入,进而推广到非线性分类问题。
- 改变了问题的复杂度。由求特征向量w转化为求比例系数a,在原始问题下,求解的复杂度与样本的维度有关,即w的维度。在对偶问题下,只与样本数量有关。
- 求解更高效,因为只用求解alpha系数,而alpha只有支持向量才非0,其它全部为0。
SVM算法优缺点总结:
- SVM算法的主要优点有:
- 解决高维特征的分类回归问题很有效,在特征维度大于样本数时依然有很好的效果。
- 仅仅使用一部分支持向量来做超平面的决策,无需依赖全部数据。
- 使用核函数可以灵活的来解决各种非线性的分类回归问题。
- 样本量不是海量数据的时候,分类准确率高,泛化能力强。
- SVM算法的主要缺点有:
- 特征维度远大于样本数时,SVM表现一般。
- SVM在样本量非常大,核函数映射维度非常高时,计算量过大,不太适合使用。
- 非线性问题的核函数的选择没有通用标准,难以选择一个合适的核函数。
- SVM对缺失数据敏感。
- SVM要进行距离计算,需要对数据进行标准化处理,而决策树不需要。
SVM和LR的异同点
- SVM和LR的相同点:
- LR和SVM都是有监督的学习
- LR和SVM都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题)
- 两个方法都可以增加不同的正则化项,如l1、l2等等。所以在很多实验中,两种算法的结果是很接近的。
- SVM和LR的不同点:
- 样本点对模型的作用不同。SVM只有关键的样本点(支持向量)对模型结果有影响,而LR每一个样本点都对模型有影响。
- 损失函数不同。SVM是hinge损失函数,LR是log损失函数。这两个损失函数的目的都是增加对分类影响较大的数据点的权重,减少与分类关系较小的数据点的权重。
- 理论基础不同。SVM基于严格的数学推导,LR基于统计,可解释性比SVM好。
- 输出不同。LR可以对每个样本点给出类别判断的概率值,SVM无法做到。
- 可处理的特征空间维度不同。LR在特征空间维度很高时,表现较差。SVM则可以通过对偶求解高效应对这一挑战。
- 防过拟合能力不同。SVM模型中内含了L2正则,可有效防止过拟合。LR要自己添加正则项。
- 处理非线性分类问题能力不同。SVM可通过核函数灵活地将非线性问题转化为线性分类问题。LR需要手动进行特征转换。
- 计算复杂度不同。对于海量数据,SVM的效率较低,LR效率比较高。
- 能力范围不同。 SVM拓展后,可解决回归问题,LR不能。
- 抗噪声数据能力不同。SVM的损失函数基于距离测度,抗噪声能力要强于LR。
为什么SVM要引入核函数?
当样本在原始空间线性不可分时,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。
令ϕ(x)表示将x映射后的特征向量,于是在特征空间中划分超平面所对应的模型可表示为:
![]()
优化的目标函数为:
其对偶问题为:
求解上式涉及到计算![]() ,这是样本xi与xj映射到特征空间之后的内积。由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算
,这是样本xi与xj映射到特征空间之后的内积。由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算![]() 通常是困难的,为了避开这个障碍,可以设想这样一个函数:
通常是困难的,为了避开这个障碍,可以设想这样一个函数:
即xi与xj在特征空间的内积等于它们在原始样本空间中通过函数K(·,·)计算的结果.有了这样的函数,我们就不必直接去计算高维甚至无穷维特征空间中的内积,于是对偶问题可重写为:
SVM常用核函数:
SVM 核函数之间的区别:
一般选择线性核和高斯核( RBF 核)。
- 线性核:主要用于线性可分的情形,参数少,速度快,对于一般数据,分类效果比较理想。
- RBF 核:主要用于线性不可分的情形,参数多,分类结果非常依赖于参数。
一般通过训练数据的交叉验证来寻找合适的参数,不过这个过程比较耗时。 如果特征的数量很大,跟样本数量差不多,选用线性核的 SVM。 如果特征的数量比较小,样本数量一般,选用高斯核的 SVM。
为什么SVM对缺失数据敏感?
SVM希望样本在特征空间中线性可分,所以特征空间的好坏对SVM的性能很重要,缺失特征数据将影响超平面距离的度量,进一步会影响训练结果的好坏。
SVM如何处理多分类问题?
直接法,直接在目标函数上修改,将多个分类面的参数求解合并到一个最优化问题里面(计算量非常大)。
间接法:对训练器进行组合。其中比较典型的有一对一(OVO),和一对多(OVR)。
一对多:将二分类学习器的两类设定为目标类为一类,其余类为另外一类,针对k个类可以训练出k个分类器,当有一个新的样本来的时候,用这k个分类器来测试,那个分类器的概率高,那么这个样本就属于哪一类。效果不太好,bias比较高。
一对一:对任意两个类训练出一个分类器,如果有k类,一共训练出C(2,k) 个分类器,当有一个新样本时,用这C(2,k) 个分类器来预测,每当被判定属于某一类的时候,该类就加一,最后票数最多的类别被认定为该样本的类。
SVM是用的是哪个库?Sklearn中的SVM都有什么参数可以调节?
采用sklearn.svm.SVC设置的参数。SVC函数的训练时间是随训练样本平方级增长,所以不适合超过10000的样本。对于多分类问题,SVC采用的是one-vs-one投票机制,需要两两类别建立分类器,训练时间可能比较长。
sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)
主要调节的参数有:C、kernel、degree、gamma、coef0:
- C:C-SVC的惩罚参数C?默认值是1.0,C越大,相当于惩罚松弛变量,希望松弛变量接近0,即对误分类的惩罚增大,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱。C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
- kernel :核函数,默认是rbf,可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
- degree :多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
- gamma : ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’,则会选择1/n_features
- coef0 :核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
Hard Margin SVM
1. 回顾感知机模型
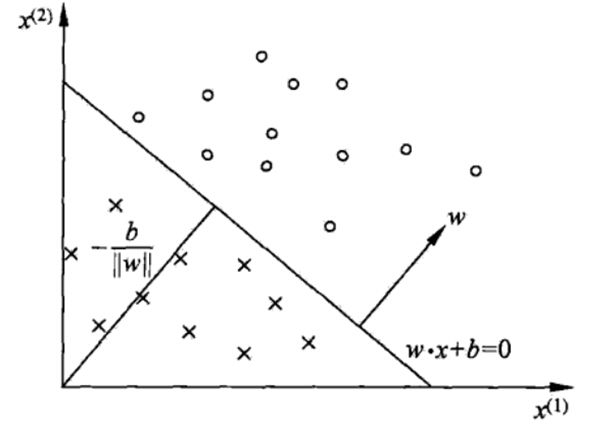
感知机的模型就是尝试找到一条直线(超平面),能够把二元数据隔离开。对于这个分离的超平面,我们定义为 ,如下图。定义在该超平面上方的点y=1 ,在该超平面下方的点y=−1。可以看出满足这个条件的超平面并不止一个。那么这么多的可以分类的超平面,哪个是最好的呢?哪个是泛化能力最强的呢?
,如下图。定义在该超平面上方的点y=1 ,在该超平面下方的点y=−1。可以看出满足这个条件的超平面并不止一个。那么这么多的可以分类的超平面,哪个是最好的呢?哪个是泛化能力最强的呢?
感知机模型的损失函数优化的思想是让所有误分类的点(定义为M)到超平面的距离和最小,即最小化下式:
当w和b成比例的增加,比如,当分子的w和b扩大N倍时,分母的L2范数也会扩大N倍。也就是说,分子和分母有固定的倍数关系。那么我们可以固定分子或者分母为1,然后求另一个即分子自己或者分母的倒数的最小化作为损失函数,这样可以简化损失函数。在感知机模型中,我们采用的是保留分子,固定分母 ,即最终感知机模型的损失函数为:
,即最终感知机模型的损失函数为:
2. 支持向量
在感知机模型中,我们可以找到多个可以分类的超平面将数据分开,并且优化时希望所有的点都离超平面远。但是实际上离超平面很远的点已经被正确分类,我们让它离超平面更远并没有意义。反而我们最关心是那些离超平面很近的点,这些点很容易被误分类,如果我们可以让离超平面比较近的点尽可能的远离超平面,那么我们的分类效果会好一些。
如下图所示,分离超平面为 =0 ,如果所有的样本不光可以被超平面分开,还和超平面保持一定的函数距离(下图函数距离为1),那么这样的分类超平面是比感知机的分类超平面优的。可以证明,这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量,我们定义为支持向量,如下图虚线所示。
=0 ,如果所有的样本不光可以被超平面分开,还和超平面保持一定的函数距离(下图函数距离为1),那么这样的分类超平面是比感知机的分类超平面优的。可以证明,这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量,我们定义为支持向量,如下图虚线所示。
![]()
3. 函数间隔与几何间隔
4. SVM模型目标函数与优化
Soft Margin SVM
1. 线性分类SVM面临的问题
有时候本来数据的确是可分的,也就是说可以用线性分类SVM的学习方法来求解,但是却因为混入了异常点,导致不能线性可分,比如下图1,另外一种情况虽线性可分,但是会严重影响我们模型的泛化预测效果,如下图2,如果不考虑异常点,SVM的超平面应该是下图中的红色线所示,但是由于有一个蓝色的异常点,导致我们学习到的超平面是图中的粗虚线所示,这样会严重影响分类模型预测效果。
如何解决这些问题呢?SVM引入了软间隔最大化的方法来解决。
2. 线性分类SVM的软间隔最大化
回顾下硬间隔最大化的条件:
3. 线性分类SVM的软间隔最大化目标函数的优化
和线性可分SVM的优化方式类似,我们首先将软间隔最大化的约束问题用拉格朗日函数转化为无约束问题如下:
利用上面的三个式子去消除w和b。
4. 软间隔最大化时的支持向量
![]()
5. 合页损失函数
线性支持向量机还有另外一种解释如下:
Kernel SVM
线性可分SVM通过软间隔最大化,可以解决线性数据集带有异常点时的分类处理,但是现实生活中的确有很多数据不是线性可分的,这些线性不可分的数据也不是去掉异常点就能处理这么简单。SVM通过引入核函数可以处理这样的情况。
1. 回顾多项式回归
多项式回归转化为线性回归:
也就是说,对于二维的不是线性的数据,将其映射到了五维以后,就变成了线性的数据。对于在低维线性不可分的数据,在映射到了高维以后,就变成线性可分的了。
2. 核函数的引入
求解上式涉及到计算样本映射到特征空间之后的内积。由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算此内积是困难的。但可假想有这样一个函数:
K(x,z)的计算是在低维特征空间来计算的,它避免了在高维维度空间计算内积的巨大计算量。总结下线性不可分时核函数的引入过程:
遇到线性不可分的样例时,常用做法是把样例特征映射到高维空间中去(如多项式回归)但是遇到线性不可分的样例,一律映射到高维空间,那么这个维度大小是会高到令人恐怖的。此时,可以引入核函数,核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数好在它在低维上进行计算,而将实质上的分类效果(利用了内积)表现在了高维上,这样避免了直接在高维空间中的复杂计算,真正解决了SVM线性不可分的问题。
3. 核函数的介绍
对于从低维到高维的映射,核函数不止一个。那么什么样的函数才可以当做核函数呢?对于任意的![]() 对应的Gram矩阵
对应的Gram矩阵 是半正定矩阵,则K(x,z)是正定核函数。
是半正定矩阵,则K(x,z)是正定核函数。
4. 分类SVM的算法小结 
SMO算法关系到,我们如何求出优化函数极小化时候的α∗,进而求出w,b我们将在下一篇讨论这个问题。
1. SVM回归模型的损失函数度量
如下图所示,在蓝色条带里面的点都是没有损失的,但是外面的点的是有损失的,损失大小为红色线的长度。
总结下,我们的SVM回归模型的损失函数度量为:
2. SVM回归模型的目标函数的原始形式
上一节我们已经得到了我们的损失函数的度量,现在可以可以定义我们的目标函数如下:
3. SVM回归模型的目标函数的对偶形式
上一节我们讲到了SVM回归模型的目标函数的原始形式,我们的目标是
看似很复杂,其实消除过程和系列第一篇第二篇文章类似,由于式子实在是冗长,这里我就不写出推导过程了,最终得到的对偶形式为: