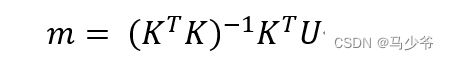相机投影矩阵的计算

摄像机标定(Camera calibration)中存在的一个关键问题：如何求解投影矩阵有了投影矩阵，我们便可以把世界坐标系变化到图像坐标系。
一、最小二乘法
已知条件
n个三维世界坐标点(保存在dat文件中)
n个二维图像坐标点(保存在dat文件中)
使用工具：
环境：windows10+python3.7+pycharm2019
第三方库：numpy

代码如下：
1. 读取dat文件
其中文件每一行都是一个三维坐标或二维坐标，因此按行读取，按列存储

# 三维
x3, y3, z3 = [], [], []
with open("data_3.dat") as f:
    for line in f:
        tmp3 = line.split()
        if tmp3:  # 防止文件空行
            x3.append(float(tmp3[0]))
            y3.append(float(tmp3[1]))
            z3.append(float(tmp3[2]))


# 二维
x2, y2 = [], []
with open("data_2.dat") as f:
    for line in f:
        tmp2 = ine.split()
        if tmp2:
            x2.append(float(tmp2[0]))
            y2.append(float(tmp2[1]))

2. 表示矩阵K(矩阵K见论文，大小为2n*11）

# 表示矩阵K
k = np.zeros((len(x3)*2, 11), dtype=int)
for i in range(len(x3)):
    k[2 * i][0], k[2 * i][1], k[2 * i][2], k[2 * i][3] = x3[i], y3[i], z3[i], 1
    k[2 * i][4], k[2 * i][5], k[2 * i][6], k[2 * i][7] = 0, 0, 0, 0
    k[2 * i][8], k[2 * i][9], k[2 * i][10] = -x2[i]*x3[i], -x2[i]*y3[i], -x2[i]*z3[i]
    k[2 * i + 1][0], k[2 * i + 1][1], k[2 * i + 1][2], k[2 * i + 1][3] = 0, 0, 0, 0
    k[2 * i + 1][4], k[2 * i + 1][5], k[2 * i + 1][6], k[2 * i + 1][7] = x3[i], y3[i], z3[i], 1
    k[2 * i + 1][8], k[2 * i + 1][9], k[2 * i + 1][10] = -y2[i] * x3[i], -y2[i] * y3[i], -y2[i] * z3[i]

3. 表示矩阵U(矩阵U见论文，大小为11*1）

U = np.zeros((len(x3)*2, 1), dtype=int)
for i in range(len(x3)):
    U[2 * i] = x2[i]
    U[2 * i + 1] = y2[i]

4.根据最小二乘法可知投影矩阵m为：

# 计算投影矩阵
m = np.matmul(np.matmul(np.linalg.inv(np.matmul(k.T, k)), k.T), U)

由于此时得到的m为11维向量，而投影矩阵大小为(3,4).根据论文中指出m(3,4)=1
因此需将1添加到m中并变换矩阵m的尺寸为3*4

list_m = []
for i in range(11):
    list_m.append(m[i][0])

list_m.append(1)
m_matrix = np.array(list_m).reshape(3, 4)

5. 验证投影矩阵m是否正确
方法：将投影矩阵与某一个三维世界坐标进行矩阵乘法运算，看看结果是否得到对应的二维图像坐标，若是，则得到正确的投影矩阵m。
由于每个人的坐标数据不一样，因此这一步可自行编写相关代码进行验证。

二、特征向量法
1. 读取dat文件
其中文件每一行都是一个三维坐标或二维坐标，因此按行读取，按列存储

# 三维
x3, y3, z3 = [], [], []
with open("data_3.dat") as f:
    for line in f:
        tmp3 = line.split()
        if tmp3:  # 防止文件空行
            x3.append(float(tmp3[0]))
            y3.append(float(tmp3[1]))
            z3.append(float(tmp3[2]))


# 二维
x2, y2 = [], []
with open("data_2.dat") as f:
    for line in f:
        tmp2 = ine.split()
        if tmp2:
            x2.append(float(tmp2[0]))
            y2.append(float(tmp2[1]))

2. 表示矩阵A(矩阵A见论文，大小为2n*12）

# 表示矩阵A(下面的k即为矩阵A)
k = np.zeros((len(x3)*2, 12), dtype=int)
for i in range(len(x3)):
    k[2 * i][0], k[2 * i][1], k[2 * i][2], k[2 * i][3] = x3[i], y3[i], z3[i], 1
    k[2 * i][4], k[2 * i][5], k[2 * i][6], k[2 * i][7] = 0, 0, 0, 0
    k[2 * i][8], k[2 * i][9], k[2 * i][10], k[2 * i][11] = -x2[i]*x3[i], -x2[i]*y3[i], -x2[i]*z3[i], -x2[i]
    k[2 * i + 1][0], k[2 * i + 1][1], k[2 * i + 1][2], k[2 * i + 1][3] = 0, 0, 0, 0
    k[2 * i + 1][4], k[2 * i + 1][5], k[2 * i + 1][6], k[2 * i + 1][7] = x3[i], y3[i], z3[i], 1
    k[2 * i + 1][8], k[2 * i + 1][9], k[2 * i + 1][10],  k[2 * i + 1][11] \
        = -y2[i] * x3[i], -y2[i] * y3[i], -y2[i] * z3[i], -y2[i]

3.计算ATA的特征值与特征向量：

# 计算ATA的特征值与特征向量
eigenvalue, featurevector = np.linalg.eig(np.matmul(k.T, k))

4.获得最小特征值的索引：

index = np.argmin(eigenvalue)

6. m(3, 4)元素归一化
由于此时得到的特征向量中的m(3, 4)并不为1，参考另一篇博文得知m(3, 4)元素值为1，因此，将m(3, 4)元素归一化(对投影矩阵操作)

m_matrix = m_matrix / m_matrix[-1, -1]

7. 验证投影矩阵m是否正确
方法：将投影矩阵与某一个三维世界坐标进行矩阵乘法运算，看看结果是否得到对应的二维图像坐标，若是，则得到正确的投影矩阵m。
由于每个人的坐标数据不一样，因此这一步可自行编写相关代码进行验证。