【GIS】常用坐标系统、高程系统
目录
坐标系统
1、概念
2、地理坐标系(Geographic Coordinate System)
(1)参考椭球体
(2)大地基准面
(3)地理坐标系
3、投影坐标系(Projected Coordinate System)
(1)投影方式
(2)分度带计算
4、常用坐标系及其转换
(1)国内常用坐标系
(2)坐标系统转换
高程系统
1、概念
2、常用高程系
(1)黄海高程系
(2)1985国家高程基准
(3)广州高程
(4)珠基高程
3、CORS系统
4、DEM
参考资料链接
坐标系统
1、概念
坐标系统,是描述物质存在的空间位置(坐标)的参照系,通过定义特定基准及其参数形式来实现。坐标是描述位置的一组数值,按坐标的维度一般分为一维坐标(公路里程碑)和二维坐标(笛卡尔平面直角坐标、高斯平面直角坐标)、三维坐标(大地坐标、空间直角坐标)。为了描述或确定位置,必须建立坐标系统,坐标只有存在于某个坐标系统才有实际的意义与具体的位置。坐标系统(Coordinate System),在ArcGIS中也被称为“空间参考(Spatial Reference)。
注:SRS:spatial reference system 空间参考系统,CRS:coordinate reference system 坐标参考系统。
地球是一个球体,球面上的位置,是以经纬度来表示,它称为“球面坐标系统”或“地理坐标系统”。
投影坐标系经由地理坐标系投影的过程,把球面坐标换算为平面直角坐标,便于印刷与计算角度与距离。
地理坐标系是球面坐标,参考平面是椭球面,坐标单位是经纬度;
投影坐标系是平面坐标系,参考平面是水平面,坐标单位是米、千米等。
地理坐标系转换到投影坐标系的过程理解为投影,即将不规则的地球曲面转换为平面。
2、地理坐标系(Geographic Coordinate System)
(1)参考椭球体
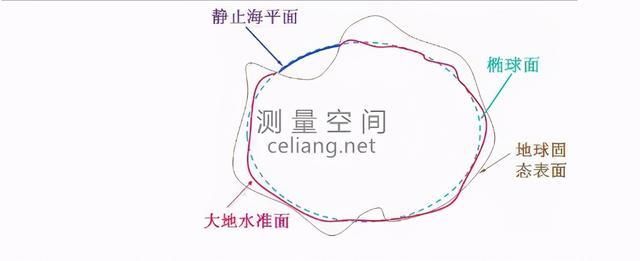
地球表面是一个凸凹不平的表面,而对于地球测量而言,地表是一个无法用数学公式表达的曲面,这样的曲面不能作为测量和制图的基准面。假想一个扁率极小的椭圆,绕地球体短轴旋转所形成的规则椭球体称之为地球椭球体。
地球椭球体与地球形体非常接近,是一个形状规则的数学表面,在其上可以做严密的计算,而且所推算的元素(如长度、角度)同大地水准面上的相应元素非常接近。
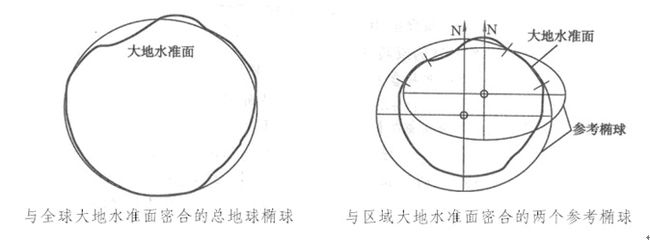
在满足地心定位和双平行条件下,确定椭球参数(长半轴、扁率)使它在全球范围内与大地体最密合的地球椭球,称为总地球椭球。
在局部区域,具有确定的椭球参数,经过局部定位和定向,同某一地区的国家大地水准面最佳拟合的地球椭球,称为参考椭球。总地球椭球和参考椭球示意图如图所示。
参心坐标系是以参考椭球的几何中心为原点,椭球定位与局部区域的大地水准面最为密合而建立的坐标系。其定义为:原点o位于参考椭球的中心,z轴平行于参考椭球的旋转轴,x轴指向起始大地子午面和参考椭球赤道的交点,y轴垂直于xoz平面,构成右手坐标系。
地心坐标系是以地球质量中心为原点的坐标系,其椭球中心与地球质心重合,且椭球定位与全球大地水准面最为密合。其定义为:原点o与地球质心重合,z轴指向地球北极,x轴指向格林尼治子午面与地球赤道的交点,y轴垂直于xoz平面,构成右手坐标系。
无论是参心坐标系还是地心坐标系均有两种表现形式:空间直角坐标系(以x、y和z表示坐标元素)和大地坐标系(以纬度b、经度l和高度h表示坐标元素)。如图所示。
地心地理坐标系统:椭球的球心=地球的质心
参心地理坐标系统:椭球的球心≠地球的质心
常用地心地理坐标系:WGS84和CGCS2000。
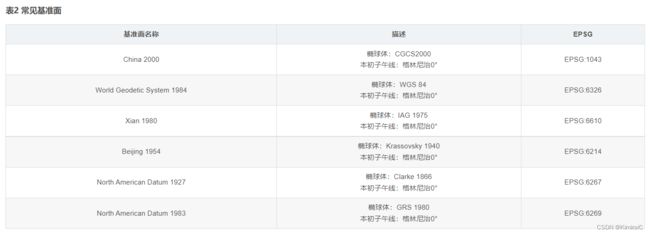
常见参心坐标系:北京54和西安80,它们的椭球体分别是克拉索夫斯基1940椭球体和IUGG1975椭球体。
(2)大地基准面
确定了一个规则的椭球表面以后,我们会发现还有一个问题,参考椭球体是对地球的抽象,因此其并不能去地球表面完全重合,在设置参考椭球体的时候必然会出现有的地方贴近的好(参考椭球体与地球表面位置接近),有地地方贴近的不好的问题,因此这里还需要一个大地基准面来控制参考椭球和地球的相对位置。 这是地球表面的第三级逼近。
大地基准面是在特定区域内与地球表面极为吻合的椭球体。
大地基准面 = 椭球体 + 本初子午线
基准面主要有两类:
地心基准面:由卫星数据得到,使用地球的质心作为原点,使用最广泛的是 WGS 1984。
区域基准面:特定区域内与地球表面吻合,大地原点是参考椭球与大地水准面相切的点,例如Beijing54、Xian80。我们通常称谓的Beijing54、Xian80坐标系实际上指的是我国的两个大地基准面。
(3)地理坐标系
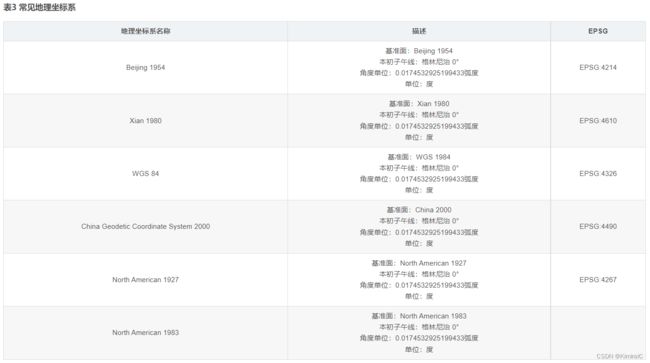
地理坐标系 = 基准面 + 本初子午线 + 角度测量单位
注:WKID即Well Known ID,众所周知的ID号的意思。EPSG是管理这些ID号的一个组织,故WKID也常称为EPSG代号。
查询网址:https://epsg.io/
UTM中投影坐标系可按下式计算
# 根据经度计算UTM区号,进而定义UTM投影
zone = str(int((longitude+180)/6) + 1)
zone = int('326' + zone) if is_north else int('327' + zone)(4)ArcGIS中的地理坐标系
在ArcGIS中地理坐标系由三个参数来定义:角度单位(Angular Unit)、本初子午线(Prime Meridian)和大地测量系统(Datum)。地理坐标系“GCS_WGS_1984”使用的角度单位为“度(Degree)”,0.0174532925199433这个数字等于“π/180”,使用的本初子午线为0.0度经线,即格林威治皇家天文台(Greenwich)所在位置的经线,使用的大地测量系统则为“D_WGS_1984”。地测量系统的最重要的参数是“椭球(Spheroid)”。椭球相同,大地测量系统不一定相同,因为原点(origin)和方位(orientation)可以不同。“D_WGS_1984”大地测量系统使用的椭球为“WGS_1984”,而“WGS_1984”椭球的“长半轴(Semimajor Axis)”和“短半轴(Semiminor Axis)”分别为6378137.0和6356752.314245179,其“反扁率(Inverse Flattening)”为298.257223563,等于Semimajor Axis/( Semimajor Axis - Semiminor Axis)。
3、投影坐标系(Projected Coordinate System)
地理坐标系经过投影后变成投影坐标系,投影坐标系因此由地理坐标系和投影组成,投影坐标系必然包括有一个地理坐标系。
投影坐标系 = 地理坐标系 + 投影方式 + 线性单位
(1)投影方式
国际间普遍采用的一种投影,是即横轴墨卡托投影(Transverse Mecator Projection),又称为高斯-克吕格投影(Gauss-Kruger Projection),在小范围内保持形状不变,对于各种应用较为方便。可以想象成将一个圆柱体横躺,套在地球外面,再将地表投影到这个圆柱上,然后将圆柱体展开成平面。圆柱与地球沿南北经线方向相切,这条切线称为“中央经线”。
我国主要采用该投影,适用于1:1万、1:2.5万、1:5万、1:10万、1:25万、1:50万比例尺的地形图。
高斯-克吕格和 UTM (UNIVERSALTRANSVERSEMERCARTORGRIDSYSTEM,通用横墨卡托格网系统)投影都是横向圆柱投影。在高斯-克吕格图中,横向圆柱与中央子午线相切,而在 UTM 图中横向圆柱切割是椭球的,这将导致在距中央子午线约 180 公里处有两个穿透圆,它们被投影成真实的长度。UTM 中的中央经线以 0.9996 的比例因子投影。
(2)分度带计算
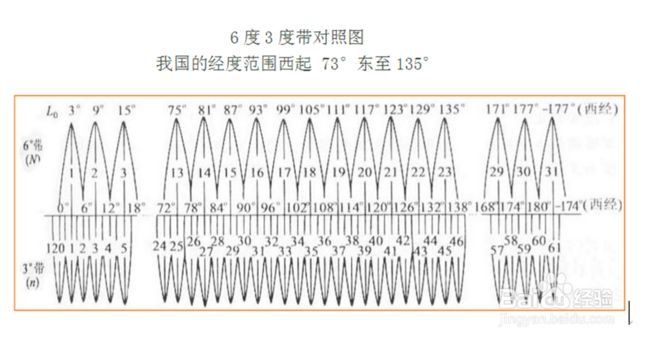
CGCS2000坐标系分度带带号计算
上图中展示的带号的分布, 我们只需要知道当前数据的地理位置,在地图软件中(如百度地图、高德)等拾取该地方的地理位置经纬度。计算方法如下:
6度带带号= 经度/6 向上取整
6度带中央经线=(6度带带号*6)-3
3度带带号=(经度-1.5°)/3 向上取整
3度带中央经线=3度带带号*3
如广州位于东经113.280637,北纬23.125178,按3度带计算,带号为38度带,中央经线为114°E。
选择CGC S2000投影坐标系:
CGCS2000_3_Degree_GK_CM_114E(无带号)
CGCS2000_3_Degree_GK_Zone_38(有带号)
WGS 1984坐标系UTM分度带带号计算
UTM是由美国制定,因此起始分带并不在本初子午线,而是在180度,因而所有美国本土都处于0-30带内。UTM投影采用6度分带,从东经180度(或西经180度)开始,自西向东算起,因此1带的中央经线为-177(-180 -(-6)),而0度经线为30带和31带的分界,这两带的分界分别是-3和3度。纬度采用8度分带,从80S到84N共20个纬度带(X带多4度),分别用C到X的字母来表示。为了避免和数字混淆,I和O没有采用。UTM的“false easting”值为500km,而南半球UTM带的“false northing”为10000km
北半球地区,选择最后字母为“N”的带;
带数=(经度整数位/6)的整数部分+31
如广州位于东经113.280637,北纬23.125178,按UTM分度带计算,带号为49度带。
选择WGS1984投影坐标系:WGS_1984_UTM_Zone_49N
4、常用坐标系及其转换
(1)国内常用坐标系
- WGS84(EPSG:4326) : 目前最流行的地理坐标系统,美国GPS就是使用的这个。一般的国外地图如谷歌地图、OpenStreetMap(OSM)均采用WGS84。
- Pseudo-Mercator(EPSG:3857) : 投影坐标系。伪墨卡托投影,也称为球体墨卡托,Web Mercator。它是基于墨卡托投影的,把 WGS84 投影到正方形。各大互联网地图公司以它为准。伪墨卡托非常适合显示数据、但不适合存储数据。一般用 WGS84 存储数据、用伪墨卡托显示数据。
- CGCS2000(4490) : 国家大地坐标系,类似于WGS84,是原始坐标系,与WGS84相近,除厘米级的高精应用外,一般可将WGS84和CGCS2000视为一样。国家背书的天地图采用CGCS2000。
- xian80(4610) : 1980年西安坐标系,又简称西安大地原点,二维坐标,现已退出历史舞台。2018年12月14日,自然资源部宣布自2019年1月1日起,全面停止向社会提供1954年北京坐标系和1980西安坐标系基础测绘成果。
- beijing54(4214) : 北京54坐标系(BJZ54),二维坐标,现已退出历史舞台。2018年12月14日,自然资源部宣布自2019年1月1日起,全面停止向社会提供1954年北京坐标系和1980西安坐标系基础测绘成果。
- GCJ02,又称火星坐标系,是我国测绘局(国测局,GCJ)制定的坐标系,由WGS84坐标系加密而成。一般的国内企业地图服务如高德地图、腾讯地图均采用GCJ02。
- BD09,即百度坐标系,是百度地图在GCJ02的基础上进行二次加密后得到的坐标系。
(2)坐标系统转换
-
ArcGIS
首先确定原始数据的坐标系,如无则需要根据经验定义坐标系,然后根据需要选择栅格或矢量工具进行坐标转换。主要使用ArcTools>Data Management Tools>Projections and Transformatios中的工具。
- 在线转换工具
千寻:千寻知位
超图:坐标转换工具 (supermapol.com)
空间投影坐标转换 (huangliuxu.com)
高程系统
1、概念
高程系统是指相对于不同性质的起算面(大地水准面、似大地水准面、椭球面等)所定义的高程体系。
高程系统采用不同的基准面表示地面点的高低,或者对水准测量数据采取不同的处理方法而产生不同的系统,分为正高、正常高、力高和大地高程等系统。高程基准面基本上有两种:一是大地水准面,它是正高和力高的基准面;二是椭球面,它是大地高程的基准面。此外,为了克服正高不能精确计算的困难还采用正常高,以似大地水准面为基准面,它非常接近大地水准面。
2、常用高程系
(1)1956黄海高程
黄海高程系以青岛验潮站1950至1956年验潮资料算得的平均海面为高程系统零点。原点设在青岛市观象山。该原点以“1956年黄海高程系”计算的高程为72.289米。
(2)1985国家高程
由于计算这个基面所依据的青岛验潮站的资料系列(1950年至1956年)较短等原因,中国测绘主管部门决定重新计算黄海平均海面,以青岛验潮站1952年至1979年的潮汐观测资料为计算依据,并用精密水准测量监测位于青岛的中华人民共和国水准原点,得出1985年国家高程基准高程和1956年黄海高程的关系:1985年国家高程基准高程=1956年黄海高程-0.029m。
(3)广州高程
广州高程 = 1985国家高程 + 4.26(米)
广州高程 = 1956黄海高程 + 4.41(米)
(4)珠基高程
根据2020年8月广东省自然资源厅http://nr.gd.gov.cn/hdjlpt/detail?pid=783420
珠江高程基准是由水利部门建立的,与1985国家高程基准的关系请咨询相关水利部门。
根据2021年12月份,广东省水利厅http://slt.gd.gov.cn/dawenku/gcjgl/content/post_3709656.html
1985国家高程=珠江基面+0.744米。
3、CORS系统
连续运行卫星定位导航服务系统(CORS) 是测绘的基础设施建设,也是信息社会、知识经济时代必备的基础设施。CORS系统使用GPS,以后可能综合应用GPS、GLONASS、GLOLILEO 和北斗系统。CORS由若干个连续运行的GPS基准站、数据处理控制中心数据传输与发播系统和移动站(用户一单台GPS接收机)组成。
使用RTK测量的高程依赖于WGS-84椭球面,所以使用RTK测量的高程属于以椭球面为起算面的大地高程。我国现在常用的1985国家高程基准(以下简称85高程)是以黄海平均海平面为统一基准面,属于以似大地水准面为起算面的正常高系统。CORS不能直接测85高程,需要转换。在有控制点的情况下,可以使用高程拟合或者求七参数的方法。如果没有控制点,则需要去当地的省/市CORS中心进行转化。
4、DEM
数字高程模型( digital elevation model ,简称DEM)是采用规则或不规则多边形拟合面状空间对象的表面,主要是对数字高程表面的描述。根据多边形的形状,可以把DEM分为两种,即格网模型和TIN模型,其中又以TIN模型运用的居多。DEM的主要优点是能够方便地进行空间的分析和计算。
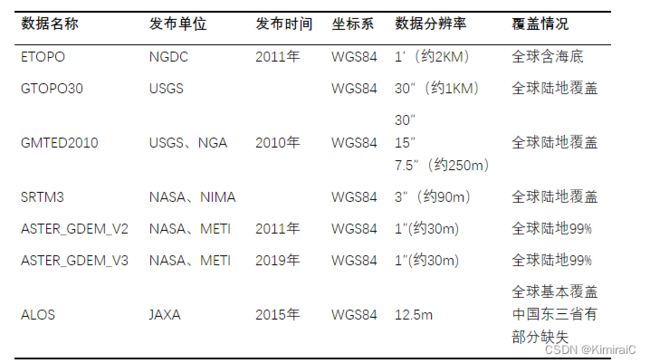
常用DEM:
一般各类公开DEM文件(非国产和自制的DEM文件),均采用WGS84坐标系,高程基准为WGS84椭球。在实际应用,如果需要用到85黄海高时,均需要通过高程控制点进行控制。因此,一般DEM提供的主要是相对高程,绝对高程需要通过处理后获得。
参考资料链接
ArcGIS中的坐标系:基本概念和常用操作
7月1日起自然资源部全面启用2000国家大地坐标系
地理坐标系与投影坐标系的区别
聊聊GIS中的坐标系|再版 详细定义、计算及高程系统
聊聊GIS中的坐标系
地理坐标系与投影坐标系区别与联系
高程系统知识汇总
千寻时空智能百科
到手的DEM不会用?教你6个常用强大功能
DEM、等高线的定义,以及使用DEM生成等高线教程