机器学习实战——决策树ID3

1. 决策树的构造

1.1 决策树的一般流程

（1）收集数据
（2）准备数据
（3）分析数据
（4）训练算法
（5）测试算法
（6）使用算法

1.2 信息熵

（1）定义

信息熵：所有类别所有可能值包含的信息期望值
$$H=-\sum _{k=1}^{2}P(x_i)lo{g}_{2}P(x_i)$$
其中，H的值越小，则集合的纯度越大。
① 约定：若p=0，则$plo{g}_{2}p=0$
② H的最小值为0（当D中所有样本属于同一类型），最大值为1（当D中样本类型的比例呈1:1分布）

（2）code：计算信息熵、创建数据集

（1）计算信息熵、创建数据

# 计算给定数据集的香农熵
from math import log

# fucn1 计算信息熵


def calcShannonEnt(dataSet):
    numEntries = len(dataSet)   # 计算实例总数
    labelCounts = {}            # 数据集存在的标签及其数量
    # (1)计算数据集中各类别的数量
    for featVec in dataSet:
        currentLabel = featVec[-1]  # eg:[1,1,'yes']
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannontEnt = 0.0
    # (2)计算熵值
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannontEnt -= prob * log(prob, 2)
    return shannontEnt

# func2 创建数据集


def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return dataSet, labels

（2）简单的测试

myDat,labels = createDataSet()
print(myDat)
print(calcShannonEnt(myDat))

结果：

[[1, 1, ‘yes’], [1, 1, ‘yes’], [1, 0, ‘no’], [0, 1, ‘no’], [0, 1, ‘no’]]
0.9709505944546686

1.3 划分数据集

按照选择的划分属性，把当前数据集划分成两份，同时删除当前属性值

（1）code：按照给定特征划分数据集

# func3 按照特征划分数据集

def splitDataSet(dataSet,axis,value):
    # 三个输入参数：待划分数据集、划分属性、特征返回值
    retDataSet = []     # 划分得到的数据集
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     # [0,axis-1]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
"""  
note: append 和 extend 的区别
a = [1,2,3]  b = [4,5,6]
a.append(b) == [1,2,3,[4,5,6]]
a.extend(b) == [1,2,3,4,5,6] 
"""

1.4 信息增益

（1）定义

离散属性$\alpha$有V个可能的取值$a^1,a^2,\dots ,a^V$，用$\alpha$来进行划分，会产生V个分支节点，其中第v各分支节点包含了D中所有在属性$\alpha$上取值为$a^V$的样本，记为$D^v$。
可以计算出用属性$\alpha$对样本D进行划分所得到的信息增益：
$$Gain(D,\alpha )=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$

（2）code：选择最好的数据集划分方法

对每个特征划分的数据集计算一次信息熵，判断按照哪个特征划分数据集获得的信息增益值最大，那个特征就是最好的划分方法。

# Fun1 选取最好的数据集划分方式  fun1+fun3
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1                     # 特征数量
    baseEntropy = calcShannonEnt(dataSet)               # 1.初始集合熵值
    bestInfoGain = 0.0                                  # 最大信息增益
    bestFeature = -1                                    # 最优划分属性
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]  # 样本中i特征的所有值
        uniqueVals = set(featList)                      # i特征的可能取值
        newEntropy = 0.0
        # i属性集合划分熵值=划分集合熵值求和
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)  
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob*calcShannonEnt(subDataSet)  # 2.划分集合的熵值
        infoGain = baseEntropy-newEntropy               # 3.信息增益
        print("第%d个特征的信息增益为%.3f" % (i,infoGain))
        # 比较得到最好的集合划分属性
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

测试函数：

# 测试部分
if __name__=='__main__':
    myDat,labels = createDataSet()
    # print(myDat)
    # print(calcShannonEnt(myDat))
    print('最佳属性划分值：',chooseBestFeatureToSplit(myDat))

结果：

第0个特征的信息增益为0.083
第1个特征的信息增益为0.324
第2个特征的信息增益为0.420
第3个特征的信息增益为0.363
最佳属性划分值： 2

1.5 递归构造决策树

（1）算法步骤

Step1： 得到原始数据集
Step2： 获得最优化分属性与对应的划分集合，获得树的分支（信息增益、集合划分）
Step3： 采用递归方法再次划分数据。其中，①当集合样本类别完全相同时，停止划分并定义为该类型的叶节点。②当遍历完所有特征时，采用多数表决法确定叶节点类型。

（2）code：创建树

# Fun2 多数表决：遍历完所有属性，类标签依然不唯一

def majorityCnt(classList):
    # 返回出现次数最多的类别名称
    classCount = {}                         # 字典：<属性,频率>
    # 1.计算属性出现频率
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    # 2.按频率降序排列
    sortedClassCount = sorted(classCount.iteritems(),
    key = operator.itemgetter[1],reverse=True)
    return sortedClassCount[0][0]

# Fun3 创建树

def createTree(dataSet,labels):
    # con1：类别完全相同 停止划分 该类别的叶节点
    classList = [example[-1] for example in dataSet]    # 所有样本的类别
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # con2：遍历完所有特征时，采用多数表决
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # 1.确定最优划分属性
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]

    # 2.划分子集并递归处理
    myTree = {bestFeatLabel:{}}
    # 2.1 删除已划分属性
    del(labels[bestFeat])
    # 2.2 计算划分属性分支
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    # 2.3 分支划分并递归处理
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    
    return myTree

测试函数：

# 测试部分
if __name__=='__main__':
    myDat,labels = createDataSet()
    # print(myDat)
    # print(calcShannonEnt(myDat))
    mytree = createTree(myDat,labels)
    print(mytree)

结果：

第1个特征的信息增益为0.324
第2个特征的信息增益为0.420
第3个特征的信息增益为0.363
第0个特征的信息增益为0.252
第1个特征的信息增益为0.918
第2个特征的信息增益为0.474
{‘有自己的房子’: {0: {‘有工作’: {0: ‘no’, 1: ‘yes’}}, 1: ‘yes’}}

1.6 测试算法：使用决策树执行分类

依靠训练数据构建了决策树之后，我们可以将它用于实际数据的分类。
（1）算法思想：
Step1： 获得当前节点的“特征”、“子树”、“特征序号”。将标签字符串转换为索引
Step2： 遍历子树所有分支，进入正确匹配的分支。当此分支仍然是子树时，递归处理该子树。当此分支为叶节点时，直接分类赋值。

（2）Code

def classify(inputTree, featLabels, testVec):
    # 1. 获得当前节点属性  dict.keys返回dict_keys 需要转化为list类型
    firstStr = list(inputTree.keys())[0]

    # 2. 获得当前节点子树
    seconDict = inputTree[firstStr]

    # 3. 特征序号
    featIndex = featLabels.index(firstStr)

    # 4. 遍历子树分支，选择进入子树、叶节点
    for key in seconDict.keys():
        # 特征值匹配，进入当前分支
        if testVec[featIndex] == key:
            # 若当前分支非叶节点，递归处理子树
            if type(seconDict[key]).__name__ == 'dict':
                classLabel = classify(seconDict[key], featLabels, testVec)
            # 无字典，则为叶节点
            else:
                classLabel = seconDict[key]
    
    return classLabel 

1.7 使用算法：决策树的存储

为了节省计算时间，最好能够在每次执行分类时调用已经构造好的决策树。
通过使用pickle序列化对象，在磁盘上保存**（二进制形式）**对象并在需要的时候读取出来。任何对象都可以执行序列化操作。
（1）决策树的存储：
需要的函数： open() , pickle.dump()

# Fun5  :  决策树的存储
# 因为以二进制形式存取，因此参数设为'wb' and 'rb'
def storeTree(inputTree,filename):
    fw = open(filename,'wb')
    pickle.dump(inputTree,fw)
    fw.close()

（2）决策树的读取
需要的函数： open() , pickle.load()

# Fun6  :  决策树的读取
def grabTree(inputTree,filename):
    fr = open(filename,'rb')
    return pickle.load(fr)

2. ID3算法(不含剪枝)代码

# 计算给定数据集的香农熵
from math import log
import operator
import pickle

from numpy.lib.nanfunctions import _nansum_dispatcher

# fucn1 计算信息熵


def calcShannonEnt(dataSet):
    numEntries = len(dataSet)   # 计算实例总数
    labelCounts = {}            # 数据集存在的标签及其数量
    # (1)计算数据集中各类别的数量
    for featVec in dataSet:
        currentLabel = featVec[-1]  # eg:[1,1,'yes']
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannontEnt = 0.0
    # (2)计算熵值
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannontEnt -= prob * log(prob, 2)
    return shannontEnt

# func2 创建数据集

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        # 1.读取,分隔的文件
        line = line.strip('\n')
        curLine = line[:].split(',')
        dataMat.append(curLine)
    return dataMat

def createDataSet():
    # 读取数据集、标签
    ''' dataSet = loadDataSet(fileName)
    labels = set([line[-1] for line in dataSet])
    return dataSet, labels '''
    dataSet=[[0, 0, 0, 0, 'no'],
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    #分类属性
    labels=['年龄','有工作','有自己的房子','信贷情况']
    #返回数据集和分类属性
    return dataSet,labels

# func3 按照特征划分数据集


def splitDataSet(dataSet, axis, value):
    # 三个输入参数：待划分数据集、划分属性、特征返回值
    retDataSet = []     # 划分得到的数据集
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]     # [0,axis-1]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet


"""  
note: append 和 extend 的区别
a = [1,2,3]  b = [4,5,6]
a.append(b) == [1,2,3,[4,5,6]]
a.extend(b) == [1,2,3,4,5,6] 
"""

# Fun1 选取最好的数据集划分方式  fun1+fun3


def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1                     # 特征数量
    baseEntropy = calcShannonEnt(dataSet)               # 1.初始集合熵值
    bestInfoGain = 0.0                                  # 最大信息增益
    bestFeature = -1                                    # 最优划分属性
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]  # 样本中i特征的所有值
        uniqueVals = set(featList)                      # i特征的可能取值
        newEntropy = 0.0
        # i属性集合划分熵值=划分集合熵值求和
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob*calcShannonEnt(subDataSet)  # 2.划分集合的熵值
        infoGain = baseEntropy-newEntropy               # 3.信息增益
        print("第%d个特征的信息增益为%.3f" % (i, infoGain))
        # 比较得到最好的集合划分属性
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

# Fun2 多数表决：遍历完所有属性，类标签依然不唯一


def majorityCnt(classList):
    # 返回出现次数最多的类别名称
    classCount = {}                         # 字典：<属性,频率>
    # 1.计算属性出现频率
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    # 2.按频率降序排列
    sortedClassCount = sorted(classCount.iteritems(),
                              key=operator.itemgetter[1], reverse=True)
    return sortedClassCount[0][0]

# Fun3 创建树


def createTree(dataSet, labels):
    # con1：类别完全相同 停止划分 该类别的叶节点
    classList = [example[-1] for example in dataSet]    # 所有样本的类别
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # con2：遍历完所有特征时，采用多数表决
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # 1.确定最优划分属性
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]

    # 2.划分子集并递归处理
    myTree = {bestFeatLabel: {}}
    # 2.1 删除已划分属性
    del(labels[bestFeat])
    # 2.2 计算划分属性分支
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    # 2.3 分支划分并递归处理
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(
            splitDataSet(dataSet, bestFeat, value), subLabels)

    return myTree

# Fun4  测试算法： 使用决策树执行分类


def classify(inputTree, featLabels, testVec):
    # 1. 获得当前节点属性  dict.keys返回dict_keys 需要转化为list类型
    firstStr = list(inputTree.keys())[0]

    # 2. 获得当前节点子树
    seconDict = inputTree[firstStr]

    # 3. 特征序号
    featIndex = featLabels.index(firstStr)

    # 4. 遍历子树分支，选择进入子树、叶节点
    for key in seconDict.keys():
        # 特征值匹配，进入当前分支
        if testVec[featIndex] == key:
            # 若当前分支非叶节点，递归处理子树
            if type(seconDict[key]).__name__ == 'dict':
                classLabel = classify(seconDict[key], featLabels, testVec)
            # 无字典，则为叶节点
            else:
                classLabel = seconDict[key]
    
    return classLabel 

# Fun5  :  决策树的存储
# 因为以二进制形式存取，因此参数设为'wb' and 'rb'
def storeTree(inputTree,filename):
    fw = open(filename,'wb')
    pickle.dump(inputTree,fw)
    fw.close()

# Fun6  :  决策树的读取
def grabTree(inputTree,filename):
    fr = open(filename,'rb')
    return pickle.load(fr)

'''  
1. 错误率：
    测试样本总量
    测试时，预测正确总量
'''

# test1：   错误率


def testError(inputTree, featLabels, testData):
    # 测试样本总数
    numEntries = len(testData)
    # 测试样本预测值
    numPre = 0
    for line in testData:
        data = line[0:-1]   # 训练数据
        reLabel = line[-1]    # 真实标签
        preLabel = classify(inputTree,featLabels,data)  # 预测标签
        if reLabel != preLabel:
            numPre +=1
    
    return float(numPre/numEntries)

    


# 测试部分c
if __name__ == '__main__':
    #   1. 训练算法
    ''' # 1.1 读取数据
    myData,Labels = createDataSet('car.txt')
    # 1.2 划分测试数据、训练数据 '''

    # 1. 训练算法
    myDat, labels = createDataSet()
    mytree = createTree(myDat, labels[:])    # 禁止函数修改总标签
    print(mytree)
    storeTree(mytree,'mytree.txt')
    # 2. 测试数据
    testVec = [0, 1, 1, 0]
    result = classify(mytree, labels, testVec)

    if result == 'yes':
        print('放贷')
    else:
        print('不放贷')

    testerr = testError(mytree,labels,myDat)
    print('测试误差 %：',testerr," %")

3. 性能度量

3.1 错误率

$$E(f;D)=\frac{1}{m}\sum _{i=1}^m⨿(f(x_i)\ne y_i)$$
解释：预测结果与实际结果不匹配的个数占总测试样本数的比例

3.2 精度

$$acc(f;D)=1-E(f;D)$$

3.3 查全率、查准率

3.3.1 混淆矩阵

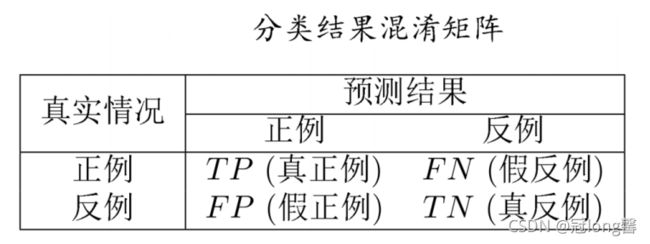
（1）理解：
TP：真正例，预测结果为阳性，且真实结果也为阳性
FP：假正例，预测结果为阳性，但真实结果为阴性
FN：假反例，预测结果为阴性，但真实结果为阳性
TN：真反例，预测结果为阴性，且真实结果为阴性

（2）关系：
设测试样本总数为m，预测为阳性的数量为$n_{+}$，预测为阴性的数量$n_{-}$，样本本身为阳性的数量$m_{+}$，样本本身为阴性的数量$m_{-}$
① $TP+FP+FN+TN=m$
② 预测为阳性的数量：$TP+FP=n_{+}$
③ 预测为阴性的数量：$FN+TN=n_{-}$
④ 样本本身阳性的数量：$TP+FN=m_{+}$
⑤ 样本本身阴性的数量：$TN+FP=m_{-}$

（3）例题：
测试样本：62个阳性，38个阴性
预测结果：48个阳性（30个正确，18个错误），52个反例
① 构造混淆矩阵：

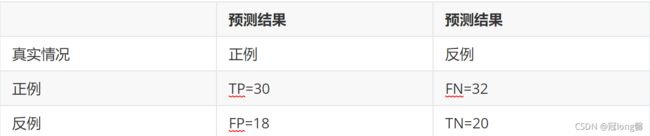
② 计算查全率、查准率
$P=\frac{30}{30+18}=0.625$
$R=\frac{30}{30+32}=0.483$

3.3.2 Code

# test2:    查准率

def testP(confusionMatrix):
    P = confusionMatrix[0][0] / (confusionMatrix[0][0]+confusionMatrix[1][0])
    return P

# test3：   查全率
def testR(confusionMatrix):
    R = confusionMatrix[0][0] / (confusionMatrix[0][0]+confusionMatrix[0][1])
    return R

4. 遇到的问题

# 1.dict.keys()返回dict_keys对象，需要转化为list类型才能使用索引值
firstStr = list(inputTree.keys())[0]

/* 2.使用pickle序列化保存对象
因为pickle以二进制存储数据，因此open文件时需要设置参数为'wb','rb'
*/
def storeTree(inputTree,filename):
    fw = open(filename,'wb')
    pickle.dump(inputTree,fw)
    fw.close()
def grabTree(inputTree,filename):
    fr = open(filename,'rb')
    return pickle.load(fr)