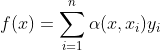注意力机制与使用了多头注意力和自注意力的transformer架构

http://zh.d2l.ai/chapter_attention-mechanisms/index.html

参考《动手学深度学习》和论文attention is all you need 理解注意力机制

---

引入

注意力的生物学解释

经过漫长进化，人具有只将注意力引向感兴趣的一小部分信息的能力。这种引向体现在视觉世界中可以分为两种，通过非自主性提示或自主性提示进行有选择地引导注意力的焦点。非自主性提示是基于环境中物体的突出性和易见性，自主性提示受认知和意识的控制。自主性的与非自主性的注意力提示解释了人类的注意力的方式， 下面我们看看如何通过这两种注意力提示， 用神经网络来设计注意力机制的框架。

如果把我们要关注一个物体（自主性）抽象为查询 ，给定任何查询query，注意力机制通过注意力汇聚将选择引导至感官输入。在注意力机制中这些感官输入被称为值value ，每个值都与一个键key配对.(有点饶）

我的理解是，想象在一个只有物体a,b,c的空间，键key表示这个空间存在的所有物体即[a,b,c],我们现在有一个念头让我们着重关注一个物品，这个念头受意识控制即前面抽象的查询query（也可以把它看成一个列表），现在有一个注意力机制（汇聚）通过匹配键和查询的相似性给出最终的值value [a',b',c']即我们想要着重关注的物体（键和查询的相似度越高最后输入的对应物体的值就越大，注意力就越集中在该物体）

定义

引用attention is all you need中的一段定义：An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

注意力机制

Nadaraya-Watson核回归是具有注意力机制的机器学习范例

考虑一个回归问题，根据输入的位置对输出y进行加权：

从注意力机制框架角度重写公式

其中x是查询，(xi,yi)是键值对。 注意力汇聚是yi的加权平均。 将查询x和键xi之间的关系建模为 注意力权重（attention weight）α(x,xi)，  这个权重将被分配给每一个对应值yi。 对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布： 它们是非负的，并且总和为1。

论文中的attention计算

dk是Q(nxdk)和K(mxdk)的维度，首先计算Q和K的转置的点积，结果除以根号下dk，对nxm的每一行做softmax ，这样每一行的值都转换到[0,1]且每一行的和为1，于是得到权重矩阵，再与V做点积得到加权和。

论文中使用的attention 机制叫做缩放点积注意力，适用于Q和K的维度相同时，当QK维度不相同可以采用加性注意力：

多头注意力

“we found it beneficial to linearly project the queries, keys and values h times with different, learned linear projections to dk, dk and dv dimensions, respectively. On each of these projected versions of queries, keys and values we then perform the attention function in parallel, yielding dv -dimensional output values. These are concatenated and once again projected, resulting in the final values”

在实践中当给定相同的查询、键和值的集合时， 我们希望模型可以基于相同的注意力机制学习到不同的行为， 然后将不同的行为作为知识组合起来， 捕获序列内各种范围的依赖关系 （例如，短距离依赖和长距离依赖关系）

因此，允许注意力机制组合使用查询、键和值的不同 子空间表示

用独立学习得到的h组不同的 线性投影（linear projections）来变换查询、键和值。 然后，这h组变换后的查询、键和值将并行地送到注意力汇聚中。 最后，将这h个注意力汇聚的输出拼接在一起， 并且通过另一个可以学习的线性投影进行变换， 以产生最终输出

​​​​​​​