基于matlab的RRT&RRT*算法实现以及可视化
学习记录-基于采样的路径规划算法
- 内容来源
- RRT
-
- 主要步骤
- 动态效果展示
- 优缺点:
- 自己进行的改进尝试
- RRT*
-
- 主要步骤
-
- NearC
- ChooseParent
- rewire
- 总结及动态效果图
- Informed RRT*
- 其他优化RRT的方式
- 总结
内容来源
记录学习深蓝路径规划课程-基于采样的路径规划一节的作业和笔记,实现基于matlab的RRT以及RRT*算法实现以及可视化。
RRT
主要步骤
- 采样:Sample
%Step 1:在地图中随机采样一个点x_rand
%提示用(x_rand(1), x_rand(2))表示环境中采样点的坐标
x_rand = randi(800, 1, 2); % 全局随机采样
- 搜索邻近节点:Near
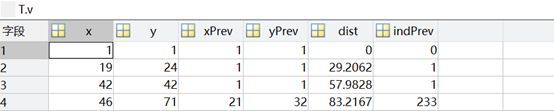
function [x_near, near_Idx] = Near(x_rand, T)
% 在树T中搜索距离随机点x_rand最近的节点,返回它及其它在树中的索引
count = size(T.v,2);
min_dis = 10000;
for node = 1: count
dis = sqrt(power((T.v(node).x-x_rand(1)) ,2) + power((T.v(node).y - x_rand(2)), 2) );
if dis<min_dis
min_dis = dis;
near_Idx = node;
x_near(1) = T.v(node).x;
x_near(2) = T.v(node).y;
end
end
end
- 生成新节点:Steer
function x_new = Steer(x_rand, x_near, StepSize)
% 将距离随机点x_rand最近的节点x_near在x_rand方向上平移StepSize的距离,生成新节点x_new
dis = distance(x_near, x_rand);
% 强迫症,想让新节点坐标为整数,fix 舍余取整(也可不取整数)
x_new(1) = fix(((dis-StepSize)*x_near(1) + StepSize*x_rand(1)) / dis);
x_new(2) = fix(((dis-StepSize)*x_near(2) + StepSize*x_rand(2)) / dis);
end
- 碰撞检测:collisionChecking(作业源码中已给-基于给定的环境图片设计的)
function feasible=collisionChecking(startPose,goalPose,map)
% 输入为两节点坐标和地图信息,若两节点直线连接不会经过障碍物,则返回true, 碰到障碍物则为返回false
feasible=true;
dir=atan2(goalPose(1)-startPose(1),goalPose(2)-startPose(2));
for r=0:0.5:sqrt(sum((startPose-goalPose).^2))
posCheck = startPose + r.*[sin(dir) cos(dir)];
if ~(feasiblePoint(ceil(posCheck),map) && feasiblePoint(floor(posCheck),map) && ...
feasiblePoint([ceil(posCheck(1)) floor(posCheck(2))],map) && feasiblePoint([floor(posCheck(1)) ceil(posCheck(2))],map))
feasible=false;break;
end
end
if ~feasiblePoint([floor(goalPose(1)),ceil(goalPose(2))],map), feasible=false; end
function feasible=feasiblePoint(point,map)
feasible=true;
if ~(point(1)>=1 && point(1)<=size(map,2) && ... % x in map
point(2)>=1 && point(2)<=size(map,1) && ... % y in map
map(point(2),point(1))==255) % x,y is Free
feasible=false;
end
- 添加新节点:AddNode
function T = AddNode(T, x_new, x_near, near_Idx)
% 将collision_free的x_new节点加入树T中,并以x_near为父节点
count = size(T.v,2) + 1;
T.v(count).x = x_new(1);
T.v(count).y = x_new(2);
T.v(count).xPrev = T.v(near_Idx).x;
T.v(count).yPrev = T.v(near_Idx).y;
T.v(count).dist=distance(x_new, x_near) + T.v(near_Idx).dist; % 该节点到原点的距离
T.v(count).indPrev = near_Idx; %父节点的index
end
- 目标节点检测
%Step 6:检查是否达到目标点附近
%提示:x_new, x_G之间的距离是否小于Thr,小于则跳出for
dis_goal = sqrt(power(x_new(1)-x_G,2) + power(x_new(2) - y_G, 2) );
if dis_goal<Thr
bFind = true;
break; % 继续采样优化所得路径
end
- 路径生成
if bFind
path.pos(1).x = x_G;
path.pos(1).y = y_G;
path.pos(2).x = T.v(end).x; path.pos(2).y = T.v(end).y;
path_cost = sqrt(power(path.pos(1).x-path.pos(2).x ,2) + power(path.pos(1).y - path.pos(2).y, 2)) + T.v(end).dist;
pathIndex = T.v(end).indPrev; % 终点索引值
j=0;
while 1
path.pos(j+3).x = T.v(pathIndex).x;
path.pos(j+3).y = T.v(pathIndex).y;
pathIndex = T.v(pathIndex).indPrev;
if pathIndex == 1
break
end
j=j+1;
end % 通过父节点索引,由终点回溯到起点
path.pos(end+1).x = x_I; path.pos(end).y = y_I; % 起点加入路径
end
动态效果展示
RRT算法在两种场景下的效果展示 normal case & narrow passage

优缺点:
专一地搜寻一条从起点到终点的路径,比PRM更有目的性一点(PRM先采样,然后在采样结果基础上后搜索寻找最优路径)
但是很显然RRT得到的路径具有随机性不是最优的,而且效率也不高
自己进行的改进尝试
优化采样函数:
显然RRT采样的方式是全局随机撒点,好处就是只要存在一条从起点到终点的路径,给他足够长的时间,它肯定能找到,这也就是probability complete的性质,但是效率很低,尤其在狭长走廊(narrow passage)的情况下。
我自己想了一种方式来优化它:
在规定的区域进行一定数量的采样,然后渐进移动到下一区域进行采样,当渐进移动到全图后,重点针对终点所在的区域撒点。以此避免全区域随机撒点效率上的不足。
对比这种采样方式和全局随机采样在两种不同环境下的效率表现:
从数据上看这种方法带来了很大程度的效率提升,在narrow passage情况下更明显,下面这个动图能更明显的表现出这种先渐进全局后重点采样方式的特点
RRT*
RRT是一种基于采样的最优化路径规划方式
与RRT的区别是,RRT尽量使新节点以及其周围的节点到起点的cost(可以是路径或者时间等目标函数)最短,而不是仅仅寻找离它近的节点,而且在找到路径后不会停止,而是继续进行采样来优化得到的路径。
主要步骤
NearC
以新节点x_new为圆心,记录与新节点之间的cost小于radius的节点以及最近节点x_near的 (集合) X_near。
这里要注意将之前搜索到的最近节点x_near也加到集合中,因为如果新节点附近radius的距离内没节点的话,之后选择父节点时就以x_near为父节点。
function nearNodes = NearC(T, x_new, near_idx)
% 找到离x_new得距离小于radius的所有节点在树中的索引, 连同near_idx一起放入nearNodes
nearNodes = [near_idx];
num = 2;
count = size(T.v,2);
radius = 60;
for Idx = 1: count
x_near = [];
x_near(1) = T.v(Idx).x;
x_near(2) = T.v(Idx).y;
dis = distance(x_near, x_new);
if dis<radius
nearNodes(num) = Idx;
num = num+1;
end
end
end
ChooseParent
在节点集合X_near中,以使得新节点到起点cost最小为基准,选择x_new的父节点。
function [x_min, min_idx] = ChooseParent(X_nears, x_new, T)
% 在邻近集合X_nears中,找到使得x_new通往起点距离最短的父节点
nearest = [];
min_cost = 10000; %计算x_new->nearest node->起点需要的cost
count = size(X_nears, 2);
for i = 1:count
nearest(1) = T.v(X_nears(i)).x;
nearest(2) = T.v(X_nears(i)).y;
cost = distance(nearest, x_new) + T.v(X_nears(i)).dist;
if cost<min_cost
min_cost = cost;
x_min = nearest;
min_idx = X_nears(i);
end
end
end
rewire
遍历x_new的邻近节点,查看它们通过x_new节点到达起点的这条路径,是不是比它们之前的路径要短,如果是则将x_new更新为它们的新父节点。
这个过程要注意,在更新父节点的之前,先要进行新路径的碰撞检测,确保路径合理性。
function T = rewire(T, X_nears, x_new, Imp)
% 对于除了最近节点x_near外的邻近节点来说 若通过x_new使其到起点的距离更短,更新x_new作为它的父节点,
count = size(X_nears, 2);
new_idx = size(T.v, 2);
for i = 2:count
pre_cost = T.v(X_nears(i)).dist;
near_node(1) = T.v(X_nears(i)).x;
near_node(2) = T.v(X_nears(i)).y;
tentative_cost = distance(near_node, x_new) + T.v(new_idx).dist; % 通过x_new到起点的cost
if ~collisionChecking(near_node, x_new,Imp) % rewire过程中也要碰撞检测
continue;
end
if tentative_cost<pre_cost % 若通过起点使cost降低,改变其父节点为x_new
T.v(X_nears(i)).xPrev = x_new(1);
T.v(X_nears(i)).yPrev = x_new(2);
T.v(X_nears(i)).dist = tentative_cost;
T.v(X_nears(i)).indPrev = new_idx;
end
end
end
总结及动态效果图
整个过程中要注意权衡NearC函数中radius变量的大小,如果过大的话在更新邻近节点父节点时,其步长可能会大于步长Delta,太小的话因为覆盖面积小,算法整体效率也会降低。
看一下动态图的展示效果

Informed RRT*
在RRT中,当初始路径已经生成之后,如果重点在初始路径周围进行采样的话,可以明显提高路径优化效率。Informed RRT就是进一步优化了采样函数,采样的方式是以起点和终点为焦点构建椭圆形采样区域。

其他优化RRT的方式
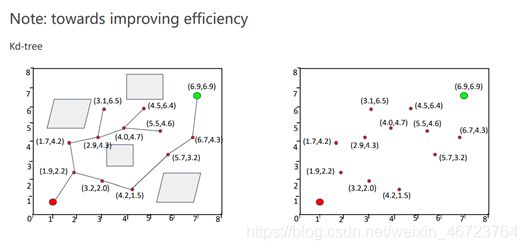
- 优化树结构-kd tree
树结构的优化会带来搜索效率上的很大提升,之前在matlab代码里Near function中搜索临近节点用的是暴力搜索,显然效率比较低,而将其优化成类似于二叉树的形式会将其搜索效率从O(n)提高为O(logn)。

- Bidirectional RRT
从起点和终点各建立一个树,当其树杈相碰时搜索结束。这种方法显然对narrow passage问题有很好的优势,而且也很新颖。


总结
RRT及其变种都是依托于采样+在树结构上加减枝的形式进行路径规划的,具有probalility complete特性,但是效率稳定性不高。不过可以针对性地对其主要函数进行优化进行效率的改进:优化采样,优化树结构等。
在文中我也提出了一些自己的简单的优化想法,有不足的地方希望和大家一起学习探讨。源码:https://github.com/Z-SB/Motion-Planning-Shenlan