逻辑(logistic)回归算法原理及两种代码实现

一. 原理简单介绍

logistic回归是一种基于线性回归模型的分类算法，常用于数据挖掘，疾病自动诊断，经济预测等领域。例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”，自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
那么为什么线性回归可以实现分类呢？
这里引进一个sigmoid函数

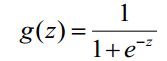
该函数图像如下：

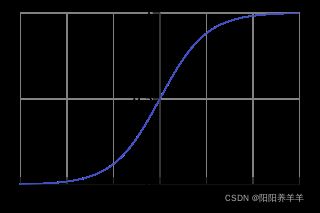
我们令$z=w_1{x}_1+w_2{x}_2+...w_n{x}_n+b$,我们规定最后若输出g(z)>0.5，则记为1。输出g(z)<0.5,则记为0，来实现分类。
具体细节不再赘述。

二.基于numpy的算法实现

①定义sigmoid函数和参数初始化函数

def sigmoid(x):
    ##输入  x：数组
    ##输出  z：经过sigmoid函数计算的值
    z = 1/(1+np.exp(-x))
    return z

def initialize_params(dims):
    ##输入    dims：参数特征维度
    ##输出  w，b
    w = np.zeros((dims,1))
    b = 0
    return w,b

②定义逻辑回归模型主体

def logistic(X,y,w,b):
    ##定义函数主体
    ##输入：X：输入矩阵  y：标签值  w：权重系数  b：偏置系数
    ##输出： loss dw  db  y_hat
    num_train = X.shape[0]   ##数据数量
    num_features = X.shape[1]  ##特征维度数
    y_hat = sigmoid(np.dot(X,w)+b)  ##模型输出
    loss = -1/num_train*np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat))  ##交叉熵损失
    dw = np.dot(X.T,(y_hat-y))/num_train
    db = np.sum(y_hat-y)/num_train
    loss = np.squeeze(loss)##压缩数组
    return y_hat,loss,dw,db
    

③定义模型训练过程（梯度下降）

def logistic_train(X,y,learning_rate,epochs):
    ##输入 X y learning_rate epochs
    ##输出 loss_list:损失列表  params:模型参数   grads参数梯度
    w,b = initialize_params((X.shape[1]))  ##初始化w和b
    loss_list = []       ##定义损失列表
    for i in range(epochs):       ##梯度下降法 
        y_hat,loss,dw,db = logistic(X,y,w,b)
        w = w-learning_rate*dw
        b = b-learning_rate*db
        if i%100 == 0:          ##每迭代一百次，记录一次损失并打印
            loss_list.append(loss)
            print('epoch %d loss %f '%(i,loss))
    params = {'w':w,'b':b}    ##保存参数
    grads = {'dw':dw,'db':db}  ##保存梯度
    return loss_list,params,grads

④定义预测函数

def predict(X,params):
    ##输入   X：输入矩阵  params：含w，b的参数字典
    ##输出 predict
    predict = sigmoid(np.dot(X.params['w'])+params['b'])
    for i in range(len(predict)):    ##输出0，1来实现分类
        if predict[i] > 0.5:
            predict[i] = 1
        else:
            predict[i] = 0
    return predict

⑤ 生成模拟二分类数据集

import numpy as np
from sklearn.datasets import make_classification    ##导入生成分类数据的库函数
X,labels = make_classification(n_samples=100,    
                              n_features=2,
                              n_redundant=0,
                              n_informative=2,
                               random_state=1,
                              n_clusters_per_class=2)   ##生成模拟二分类数据集
rng = np.random.RandomState(2)   ##设置随机数种子
X += 2*rng.uniform(size=X.shape)  ##对生成的随机数添加一组均匀分布噪音

此处可用其他分类数据集代替。

⑥划分训练集和测试集

offset = int(X.shape[0]*0.8)  ##按0.8比例得到数据数量
X_train,y_train = X[:offset],labels[:offset]
X_test,y_test = X[offset:],labels[offset:]
y_train = y_train.reshape((-1,1))  ##转化成一列数据
y_test = y_test.reshape((-1,1)) 

⑦模型训练和预测

loss_list,params,grads = logistic_train(X_train,y_train,0.01,1000) ##调用模型
print(params)   ##打印参数w和b
y_pred = predict(X_test,params)   ##预测
print(y_pred)

⑧模型效果评估

from sklearn.metrics import classification_report
print(classification_report(y_test,y_pred))  ##打印评估报告

三.基于sklearn的算法实现

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
clf = LogisticRegression(random_state=0).fit(X_train,y_train)  ##定义模型并直接拟合
y_pred = clf.predict(X_test)
print(y_pred)
print(classification_report(y_test,y_pred))  ##打印评估报告