小样本深度学习图像识别
深度学习方法极度依赖大规模标注数据, 这一缺陷极大地限制了深度学习方法在实际图像识别任务中的应用。
因此我们提出了小样本的图像识别
小样本图像识别任务需要机器学习模型在少量标注数据上进行训练和学习, 目前经常研究的问题为N-way K-shot形式, 即问题包括N种数据, 每种数据只包含K个标注样本. 现有的小样本图像识别问题可以看做是基于深度迁移学习的图像识别问题, 这里我们把上面提到的少量标注数据称作目标数据域, 后续的识别任务都是基于目标数据所包含的类别进行的; 然后为了辅助模型的训练, 通常会引入一个和目标数据域类别互斥的辅助数据集, 和目标数据域的少量标注相反, 辅助数据集的标注样本更加丰富, 类别也更加多.
解决N-way K-shot形式的小样本图像识别任务, 大多数方法会从辅助数据集学习先验知识, 然后在标注有限的目标数据域上利用这些先验知识完成学习和预测任务.
1通过生成伪数据来填充标注不足的小样本数据, 是数据增强最常见的思路. 在传统的图像处理任务中, 裁剪、旋转、锐化等方法经常用来提升图像样本的多样性, 这些简单的图像增强方法可以有效地避免模型过拟合, 提升算法性能. 但是这些简单的图像增强的方法并不能有效地改善小样本学习任务的识别性能, 其中最主要的原因就是传统的数据增强方法不能很好地帮助模型度量新类(少量标注类别)的类内差异. 比如训练数据中包含了鸟这一类别, 但是提供的数据过少, 大多都是鸟站立在枝头的图片, 那么在测试的时候, 对于飞翔在天空的鸟的图片, 模型是很难正确分类的. 为了解决这样的问题, 一个直观的方法就是学习标注充分的同一类别数据之间的模式, 然后把这种模式应用在少量标注样本上, 产生可以较好地刻画该类类内差异的伪数据.
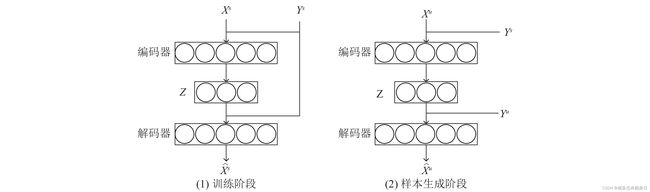
上图中样本 Xs 和 Ys 来自标注充分的基类数据: Xs 是标注充分的基类数据的输入样本, Ys 是对应的分类标签, 样本 Yu 是只有少量标注的新类数据的分类标签,
算法的基本流程是:
(1)在模型的训练阶段, 使用采样样本 Xs 和对应的标签 Ys 来训练自编码网络模型, 这和之前的自编码网络模型不同之处是, 该模型解除了对中间特征Z的维度的限制, 使得在解码阶段, 自编码器会更多地“依赖”解码阶段的辅助数据 Ys , 从而使得样本生成阶段, 生成的样本 X^s 即编码了同一类别的样本 Xs 和 Ys 的类内差异, 同时也编码了新类数据 Yu 的信息.
(2)在模型的生成阶段, 将采样数据 Xs 和新类的分类标签 Yu 输入训练好的自编码器, 此时自编码器利用给定的分类标签 Yu 的信息, 让输入的原始数据 Xs 转变为具有新类数据特征的生成样本 X^u , 从而完成数据增强的任务.
(3)在模型的测试阶段, 我们经过了前面的编码器训练和伪数据生成阶段, 在测试的时候, 我们将生成的用于数据增强的数据和原始的小样本数据一块输入算法模型, 对原有的识别模型进行微调, 使其能够是识别新类别的数据.
下面详细介绍一下TriNet的算法流程, 即TriNet模型如何训练以及生成用于数据增强的伪数据.
(1)首先通过ResNet-18网络模型提取输入图片的多级深度特征, 深度特征从浅层到深层, 分别对应了左边蓝色虚线框中的Layer1、Layer2、Layer3和Layer4;
(2)然后将上一步提到到的多级深度特征输入TriNet的编码器, 即图2中左边的虚线三角形部分, 该部分主要包含了3种基本操作: 绿色箭头表示串联的卷积操作和最大池化操作, 红色箭头表示卷积操作, 紫色的箭头表示全连接操作, 即矩阵变换操作. TriNet通过上面3种基本操作, 将多级深度特征映射到语义空间;
(3)通过TriNet编码器映射得到的语义空间是和标签的语义空间对齐的, 即狮子类(Lion)数据和猫类(Cat)数据的标签语义是相似的(这里的标签语义可以通过预训练的自然语言处理词向量模型得到), 那么TriNet编码器映射得到的狮子类语义特征在语义空间中, 是和猫类的语义特征相近的;
(4)利用上面语义空间的性质, TriNet模型在语义空间中寻找和输入语义特征最相似的另一个类别的语义特征, 并给其施加一定范围的高斯噪声, 输入下游的TriNet解码器模块;
(5) TriNet解码器和TriNet编码器结构类似, 都是通过前面提到的3种基本操作构成的, 但是输入输出和编码器刚好相反, 即此时解码器输入的是语义空间的语义特征, 输出得到ResNet-18模型特征空间的深度特征. 此时解码器输出的深度特征就可以作为输入类别的伪数据, 完成数据增强任务.

经过充分的训练, TriNet可以生成足够的伪数据, 将其补充进入只有少量标注的类别中, 然后我们将进行数据增强后的新任务数据输入之前预训练的识别模型, 通过微调的方法使得模型可以适应新的识别任务. 在后续的测试阶段, 我们直接将待识别的数据输入经过微调的模型, 通过识别模型的输出预测类别.
2基于迁移学习的小样本图像识别方法
面对标注限制的机器学习任务, 一个很自然的思路就是将模型在大数据集上进行预训练, 从中学习到一些有利于当前任务的先验知识, 从而来弥补标注数据不足的问题.
这里就拿在图像处理领域经常使用的卷积神经网络来举例说明. 众所周知, 卷积神经网络是通过多次卷积运算堆叠, 从图像数据中逐层提取特征, 并最终得到一个维度更低, 更利于后续全连接层的特征嵌入. 卷积神经网络为什么可以实现这么好的图像处理性能, 一直是学术界普遍关注的一个问题. 其中人们普遍认可的一个观点是, 卷积神经网络中特征的复杂性是随网络深度加深而提高的。

可以看到底层的神经网络学习到普遍是一些通用特征, 然后随着网络层数的加深, 特征逐渐变得特定化, 比如这里是一个人脸检测的算法, 随着网络层数的加深, 特征逐渐可以描述人的五官, 最后甚至可以表示一整张人脸信息.
对于图像处理任务而言, 用相似的网络结构模型来处理不同的任务, 网络前几层的特征一般都是相似的, 即是任务无关的, 比如卷积神经网络的卷积层参数一般是可以在不同任务之间共享的, 这也就是为什么有的网络模型训练之初会使用一些规模较大、数据质量较高的数据集来进行预训练初始化参数的原因; 然后网络的高层特征, 以及特征提取后续的全连接层则更多地编码了任务特定信息, 不适合在任务之间共享, 需要使用目标数据来进行调整.
深度神经网络的迁移学习方法中, 微调的方法几乎是最直观也最有效的方法. 微调的一个基本的流程如下.
(1)在一个数据量充足的大数据集上进行预训练;
(2)对应目标数据, 固定底层的特征权重, 只对网络高层的权重使用目标数据进行反向传播更新;
基于微调的方法步骤简单, 目前不少基于微调的方法在小样本问题上都取得了不错的效果, 下面的内容详细介绍了其中两种比较有代表性的方法.
使用了如下的损失函数: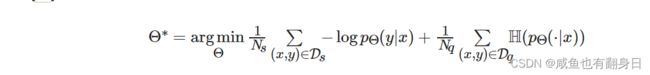
其中, 符号 Θ 代表模型参数, Ns 是支持集样本数量, Ds 是支持集样本, pΘ 是模型函数, Nq 是查询集样本数量, Dq 是查询集样本. 损失函数的前半部分就是分类任务中常见的交叉熵损失函数, 后半部分的正则项则相对来说比较陌生. 这里首先介绍一下香农熵的概念, 香农熵是用来度量随机变量的不确定性, 也就是这个随机变量所含有的信息量大小的. 对于一个随机变量X, 它的香农熵定义如下:
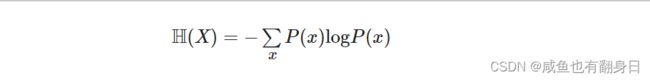
其中, 符号 H(X) 是随机变量的香农熵, P(x) 代表随机变量的概率分布. 如果这个随机变量的分布相对集中, 则所含的信息量就较少(不确定性较低), 此时香农熵就会较低; 如果这个随机变量的分布相对均匀, 极端情况下为均匀分布, 此时该随机变量的信息量就较高, 香农熵也会较高. 因此这里使用当前的网络模型对查询集上的无标签数据打上的预测得到的伪标签, 来度量模型所编码的信息量.
(1)伪标签的各个类别预测概率分布均匀, 则说明此时的网络模型并不能对查询集中的样本给出一个较好的预测, 所以需要惩罚模型;
(2)反之则说明模型可以较好地对新数据进行预测, 信息量或者说混乱程度更低, 此时正则项较小, 不影响模型更新.
这种方法显式地将查询集中的无监督信息编码进行了网络模型, 使得网络预测结果趋于概率集中