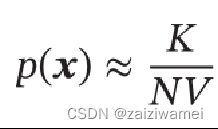第9章 无监督学习
系列文章目录
第1章 绪论
第2章 机器学习概述
第3章 线性模型
第4章 前馈神经网络
第5章 卷积神经网络
第6章 循环神经网络
第7章 网络优化与正则化
第8章 注意力机制与外部记忆
第9章 无监督学习
第10章 模型独立的学习方式
第11章 概率图模型
第12章 深度信念网络
第13章 深度生成模型
第14章 深度强化学习
第15章 序列生成模型
文章目录
- 系列文章目录
- 前言
- 9.1 聚类
-
- 9.1.1 聚类概述
-
- 1. 含义
- 2. 样本间距离、相似性
- 3. 聚类任务
- 4. 类/簇（cluster）
- 5.常用的聚类方法
- 6.聚类效果评价指标
- 9.1.2 K均值方法
-
- 1. 三类样本的聚类过程
- 2. 聚类的算法过程
- 3. 目标函数
- 4. K-均值聚类的超参数选择
- 5. 优缺点
- 9.1.3 层次聚类
-
- 1. 含义
- 2. 聚合的聚类过程
- 3. 分裂聚类过程
- 4. 优缺点
- 9.2 无监督特征学习
-
- 9.2.1 主成分分析(Principal Component Analysis，PCA)
-
- 1. 优化准则
- 2. 数据降维的方法
- 3. 目标函数
- 9.2.2 编码与稀疏编码
-
- 1. 编码含义
- 2. 完备性
- 3. 稀疏编码（Sparse Coding）
- 4. 训练过程
- 5. 稀疏编码的优点
- 9.2.3 自编码器
-
- 1. 含义
- 2. 目标函数
- 3. 两层网络结构的自编码器
- 4. 稀疏自编码器
- 5.降噪自编码器
- 9.2.4 自监督学习
- 9.3 概率密度估计
-
- 9.3.1 参数密度估计（Parametric Density Estimation）
-
- 1. 概述
- 2. 正态分布与多项分布
- 3. 参数密度估计存在问题
- 9.3.2 非参数密度估计（Nonparametric Density Estimation）
-
- 1.概述
- 2. 直方图方法
- 3. 核密度估计（Kernel Density Estimation）
- 4. K近邻方法
- 9.4 半监督学习
-
-
- 1. 自训练（Self-trainning）
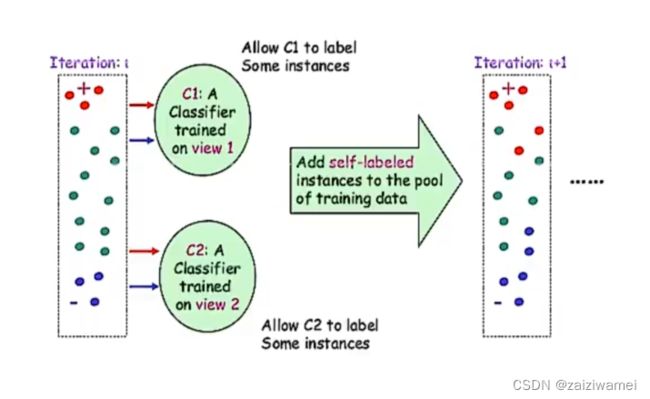
- 2. 协同训练（Co-trainning）
-
- 总结
前言
无监督学习（Unsupervised Learning，UL） 是指从无标签的数据中学习出一些有用的模式。无监督学习算法一般直接从原始数据中学习，不借助于任何人工给出标签或者反馈等的指导信息。如果监督学习是建立输入-输出之间的映射关系，那么无监督学习就是发现隐藏的数据中的有价值信息，包括有效的特征、类别、结构以及概率分布等。
典型的无监督学习问题可以分为以下几类：
- 无监督特征学习（Unsupervised Feature Learning） 是从无标签的训练数据中挖掘有效的特征或表示．无监督特征学习一般用来进行降维、数据可视化或监督学习前期的数据预处理．特征学习也包含很多的监督学习算法，比如线性判别分析等．
- 概率密度估计（Probabilistic Density Estimation） 简称密度估计，是根据一组训练样本来估计样本空间的概率密度．密度估计可以分为参数密度估计和非参数密度估计．参数密度估计是假设数据服从某个已知概率密度函数形式的分布（比如高斯分布），然后根据训练样本去估计概率密度函数的参数．非参数密度估计是不假设数据服从某个已知分布，只利用训练样本对密度进行估计，可以进行任意形状密度的估计．非参数密度估计的方法有直方图、核密度估计等．
- 聚类（Clustering） 是将一组样本根据一定的准则划分到不同的组（也称为簇（Cluster））．一个比较通用的准则是组内样本的相似性要高于组间样本的相似性．常见的聚类算法包括K-Means算法、谱聚类等。
9.1 聚类
9.1.1 聚类概述
1. 含义
将样本集合中相似的样本分配到相同的类/簇（cluster），不相似的样本分配到不同的类/簇，使得类内样本间距较小而类间样本间距较大。
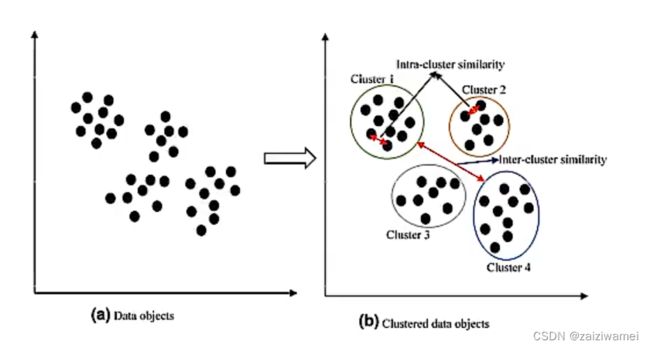
2. 样本间距离、相似性
常用的评价样本间距离、相似性的指标有 L1、L2距离， 余弦距离，相关系数 、汉明距离（比较样本每一维之间的距离）
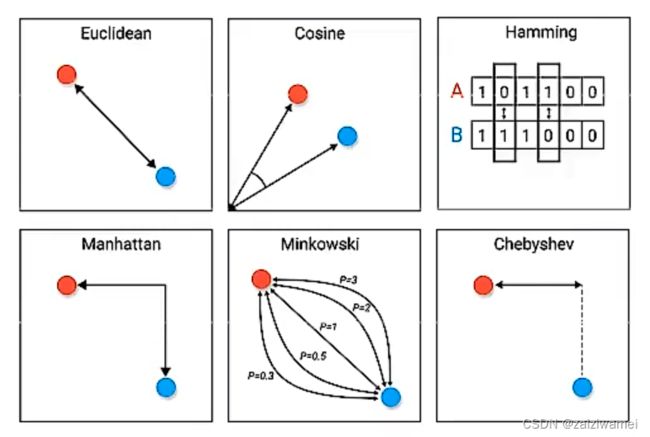
3. 聚类任务
常用的任务有图像分隔、文本聚类、社交网络分析等。
4. 类/簇（cluster）
类/簇没有一个严格的定义，可以理解为一组相似的样本。
类内间距：同一组相似样本内部个体之间的距离，包括
样本间平均距离：
a v g ( C ) = 2 ∣ C ∣ ( ∣ C ∣ − 1 ) ∑ 1 ≤ i ≤ j ∣ C ∣ d i j avg(C)=\frac{2}{|C|(|C|-1)}\sum_{1\leq i\leq j|C|}d_{ij} avg(C)=∣C∣(∣C∣−1)21≤i≤j∣C∣∑dij
样本间最大距离：
d i a ( C ) = m a x 1 ≤ i ≤ j ∣ C ∣ d i j dia(C)=max_{1\leq i\leq j|C|}d_{ij} dia(C)=max1≤i≤j∣C∣dij
类间距离：不同组样本中个体之间的距离，包括
样本间最短距离：
D p q = m i n { d i j ∣ x ( i ) ∈ C p , x ( j ) ∈ C q } D_{pq}=min\{d_{ij}|x^{(i)}\in C_p,x^{(j)}\in C_q\} Dpq=min{dij∣x(i)∈Cp,x(j)∈Cq}
样本均值距离间距离：
D p q = d μ p μ q D_{pq}=d_{\mu_p\mu_q} Dpq=dμpμq
μ p 与 μ q \mu_p与\mu_q μp与μq为两个类的平均值
5.常用的聚类方法
K均值聚类、层次聚类、密度聚类、谱聚类
6.聚类效果评价指标
有外部（external index）参考结果的情况下，常用的指标有Jaccard系数（Jaccard Coefficient）、FM指数（Fowlkes and Mallows Index）、Rand指数（Rand Index）
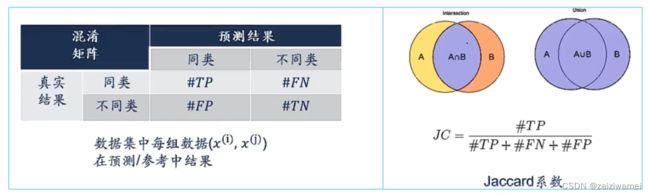
无外部（external index）参考结果的情况下，常用的指标有DB参数(Davies-Bouldin Index)、Dunn参数(Dunn Index)
9.1.2 K均值方法
1. 三类样本的聚类过程
2. 聚类的算法过程
1）选择K个点作为聚类中心
- a）根据与聚类中心的距离对每个样本点进行聚类
- b）求每类样本的平均值作为该类别的新的聚类中心
2）不断迭代a）、b）步直至收敛（比如，每个样本的类别不再改变）
3. 目标函数
目标函数：
E = ∑ i = 1 k ∑ x ∈ C i ∣ ∣ x − μ i ∣ ∣ 2 2 E=\sum_{i=1}^k\sum_{x\in C_i}||x-\mu_i||_2^2 E=i=1∑kx∈Ci∑∣∣x−μi∣∣22
其中：
- μ i 为 第 i 个 簇 C j 的 均 值 向 量 \mu_i为第i个簇C_j的均值向量 μi为第i个簇Cj的均值向量；
- E值刻画了簇内样本围绕簇均值向量的紧密程度。
收敛性：
属于NPHard问题，但可以进行迭代优化，
- 固定均值向量，优化划分→a）步
- 固定划分，优化均值向量→b）步
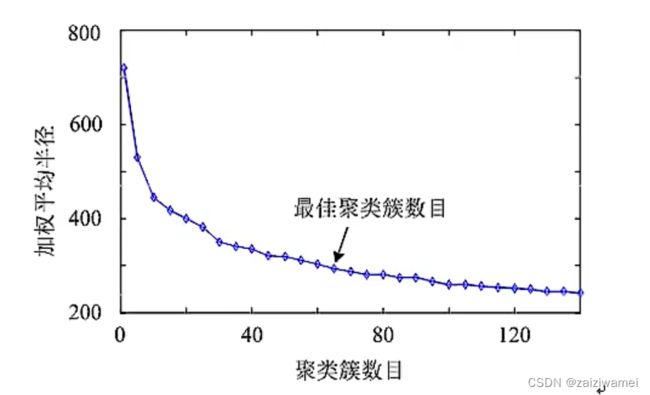
4. K-均值聚类的超参数选择
-
K的选择：
K为聚类的类的数量，选择过了加权平均值剧烈变化阶段的值作为K。
-
类中心初始化：
类中心初始化的方法包括：
- 选择大于最小间距的随机点/样本点；
- 选择K个相互距离最远的样本点；
- 选择K个等距网格点。
5. 优缺点
优点：实现简单，时间复杂度低；
缺点：K值选择困难，主要适合凸集数据，初始值对后续结果影响较大
9.1.3 层次聚类
1. 含义
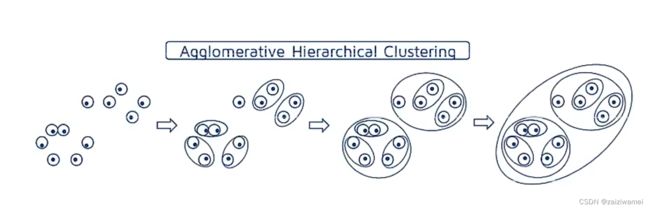
层次聚类通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类数，采用自底向上的聚合方法或自顶向下的分裂方法。
2. 聚合的聚类过程
- 将每个样本分到单独的类。
- 不断迭代计算两两类簇之间的距离，找到距离最小的两个类簇c1和c2;合并类簇c1和c2为一个类簇。
- 满足最终条件停止迭代。
3. 分裂聚类过程
- 将所有样本划分到同一个类
- 不断迭代下面过程，直至满足终止条件
– 在同一个类簇（计为c）中计算两两样本之间的距离，找出距离最远的两个样本a，b
– 将样本a，b分配到不同的类簇cl和c2中
– 计算原类簇（c）中剩余的其他样本点和a，b的距离，若是dis（a）
4. 优缺点
简单，理解容易(优点)
合并点/分裂点选择不太容易合并
分类的操作不能进行撤销
大数据集不太适合
执行效率较低 O ( T N 2 ) O(TN^2) O(TN2),T为迭代次数，N为样本点数
9.2 无监督特征学习
含义
指从无标注的数据中自动学习有效的数据表示，从而能够帮助后续的机器学习模型更快速地达到更好的性能。
目的：
特征提取、去噪、降维、数据可视化
9.2.1 主成分分析(Principal Component Analysis，PCA)
由于数据存在维度较高、在运算中存在维数灾难的问题；数据存在冗余性，导致学习效果差的问题，所以我们要想办法对数据进行降维。
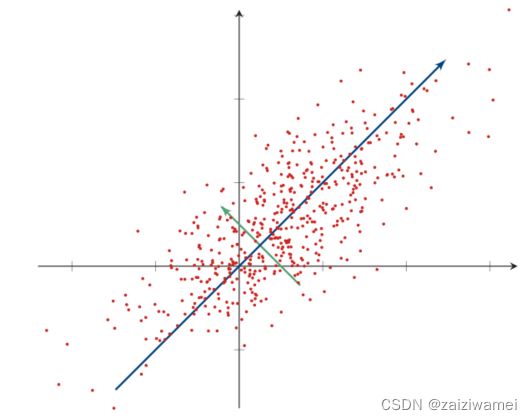
1. 优化准则
最大投影方差：使得在转换后的空间中数据的方差最大，尽可能多地保留原数据信息；
最小重构误差：在转化后空间中的数据在反向转换到原始空间时误差最小。
2. 数据降维的方法
线性投影
z = W T x ( W 满 足 W T W = I , 具 体 为 W i W i T = 1 , W i W j T = 0 ) z = W^Tx \\(W满足W^TW=I,具体为W_iW_i^T=1,W_iW_j^T=0) z=WTx(W满足WTW=I,具体为WiWiT=1,WiWjT=0)
3. 目标函数
样本点 x ( n ) x^{(n)} x(n)投影之后的表示为:
z ( n ) = w T x ( n ) z^{(n)}=w^Tx^{(n)} z(n)=wTx(n)
所有样本投影后的方差为:
目标函数:
最大化投影方差(; )并满足 T = 1 ^T = 1 wTw=1，利用拉格朗日方法转换为无约束优化问题
其中为拉格朗日乘子．对上式求导并令导数等于0，可得:
∑ w = λ w \sum w = \lambda w ∑w=λw
从上式可知，是协方差矩阵的特征向量，为特征值．同时
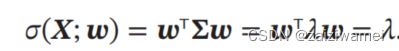
如果要通过投影矩阵 ∈ × ′ ∈ ^{×′} W∈RD×D′ 将样本投到 ′ 维空间，投影矩阵满足 T ^T WTW = 为单位阵，只需要将的特征值从大到小排列，保留前′ 个特征向量，其对应的特征向量即是最优的投影矩阵：
∑ W = W d i a g ( λ ) \sum W =W diag(\lambda) ∑W=Wdiag(λ)
其中 λ = [ λ 1 , ⋯ , λ ′ ] \lambda = [\lambda_1, ⋯ ,\lambda_{′ }] λ=[λ1,⋯,λD′]为 的前′ 个最大的特征值。
9.2.2 编码与稀疏编码
1. 编码含义
给定一组基向量 A = [ a 1 , ⋅ ⋅ ⋅ , a M ] A = [a_1 ,··· ,a_M] A=[a1,⋅⋅⋅,aM]，将输入样本x 表示为如下基向量的线性组合。
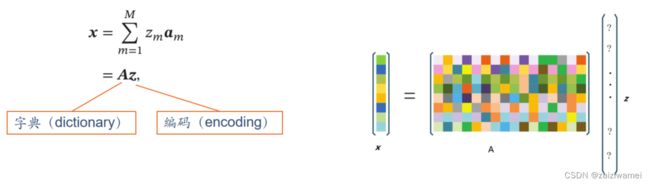
其中基向量的系数 = [ 1 , ⋯ , ] = [_1, ⋯ , _] z=[z1,⋯,zM]称为输入样本 的编码（Encoding），基向
量称为字典（Dictionary）。
2. 完备性
3. 稀疏编码（Sparse Coding）
给定一组N 个输入向量x(1),…,x(N)，其稀疏编码的目标函数定义为：
ρ(z)是一个稀疏性衡量函数，η是一个超参数，用来控制稀疏性的强度。
对于一个向量 ∈ R \inℝ^ z∈RM，其稀疏性定义为非零元素的比例．如果一个向量只有很少的几个非零元素，就说这个向量是稀疏的．稀疏性衡量函数()是给向量一个标量分数．越稀疏，()越小。
l 0 l_0 l0范数：指向量中非0的元素的个数,即 I （ ∣ z i ∣ > 0 ） I（|z_i|>0） I（∣zi∣>0）。
含义：找到一组“过完备”的基向量（即M>D）来进行编码。
4. 训练过程
给定一组 个输入向量 { ( ) } = 1 \{^{()}\}^_{=1} {x(n)}n=1N，需要同时学习基向量 以及每个输入样本对应的稀疏编码 { z ( ) } = 1 \{z^{()}\}^_{=1} {z(n)}n=1N。稀疏编码的训练过程一般用交替优化的方法进行。
5. 稀疏编码的优点
和基于稠密向量的分布式表示相比，稀疏编码具有的优点如下：
-
计算量：稀疏性带来的最大好处就是可以极大地降低计算量。
-
可解释性：因为稀疏编码只有少数的非零元素，相当于将一个输入样本表示为少数几个相关的特征。这样我们可以更好地描述其特征，并易于理解。
-
特征选择：稀疏性带来的另外一个好处是可以实现特征的自动选择，只选择和输入样本相关的最少特征，从而可以更好地表示输入样本，降低噪声并减轻过拟合。
9.2.3 自编码器
1. 含义
自编码器（Auto-Encoder，AE）是通过无监督的方式来学习一组数据的有效编码（或表示）。
假设有一组 维的样本 ( ) ∈ R , 1 ≤ ≤ ^{()} ∈ ℝ^, 1 ≤ ≤ x(n)∈RD,1≤n≤N，自编码器将这组数据映射到特征空间得到每个样本的编码 ( ) ∈ R , 1 ≤ ≤ ^{()} ∈ ℝ^, 1 ≤ ≤ z(n)∈RM,1≤n≤N，并且希望这组编码可以重构出原来的样本。
2. 目标函数
自编码器的学习目标是最小化重构错误（Reconstruction Error）:
3. 两层网络结构的自编码器
捆绑权重:
其中 ( 1 ) , ( 2 ) , ( 1 ) , ( 2 ) ^{(1)},^{(2)}, ^{(1)}, ^{(2)} W(1),W(2),b(1),b(2)为网络参数，(⋅) 为激活函数．如果令 ( 2 ) 等 于 ( 1 ) ^{(2)} 等于 ^{(1)} W(2)等于W(1)
的转置，即 ( 2 ) = ( 1 ) T ^{(2)} = ^{(1)^T} W(2)=W(1)T，称为捆绑权重（Tied Weight）。捆绑权重自编码器的参数更少，因此更容易学习。此外，捆绑权重还在一定程度上起到正则化的作用．
4. 稀疏自编码器
含义：
通过给自编码器中隐藏层单元z加上稀疏性限制，自编码器可以学习到数据中一些有用的结构。
目标函数:
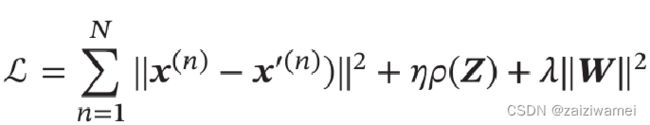
W表示自编码器中的参数。
优缺点：
和稀疏编码一样，稀疏自编码器的优点是有很高的可解释性，并同时进行了隐式的特征选择。
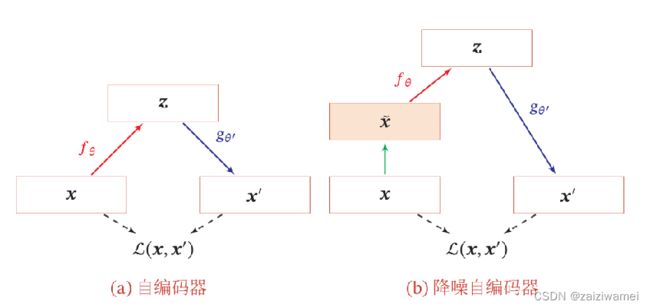
5.降噪自编码器
通过引入噪声来增加编码鲁棒性的自编码器
- 对于一个向量x，我们首先根据一个比例µ随机将x的一些维度的值设置为0，得到一个被损坏的向量x ̃。
- 然后将被损坏的向量x ̃输入给自编码器得到编码z，并重构出原始的无损输入x 。
9.2.4 自监督学习
学习目标不再只是以输入重构作为目标，在无标签样本自身寻找更多样的“目标”。
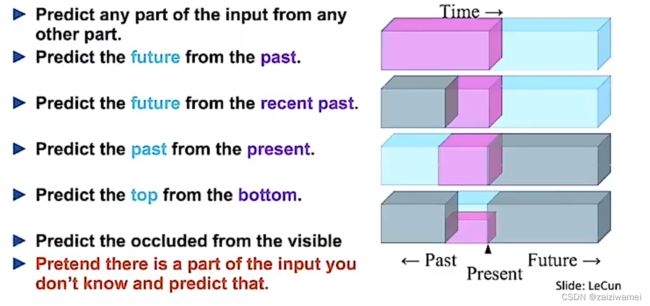
图像任务中的自监督学习—旋转角度预测
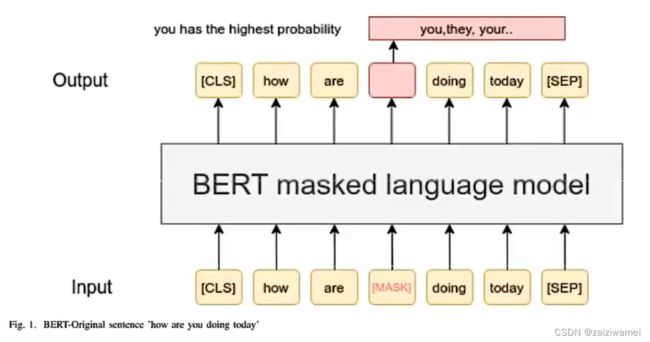
文本任务中的自监督学习—掩码语言模型（Masked Language Model）
9.3 概率密度估计
9.3.1 参数密度估计（Parametric Density Estimation）
1. 概述
含义：根据先验知识假设随机变量服从某种分布，然后通过训练样本来估计分布的参数。
估计方法：最大似然估计。
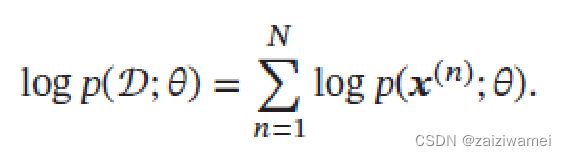
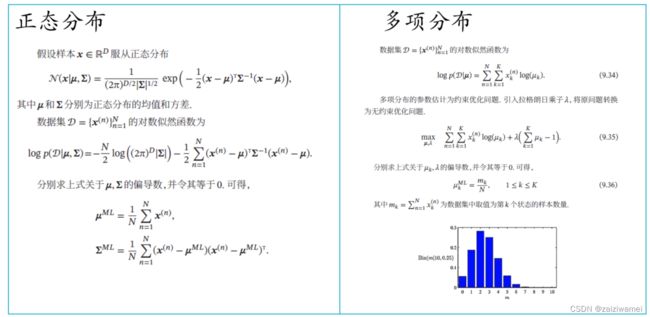
2. 正态分布与多项分布
3. 参数密度估计存在问题
-
模型选择问题，如何选择数据分布的密度函数？实际数据的分布往往是非常复杂的，而不是简单的正态分布或多项分布。
-
不可观测变量问题，即我们用来训练的样本只包含部分的可观测变量，还有一些非常关键的变量是无法观测的，这导致我们很难准确估计数据的真实分布。
-
维度灾难问题，高维数据的参数估计十分困难，随着维度的增加，估计参数所需要的样本数量指数增加。在样本不足时会出现过拟合。
9.3.2 非参数密度估计（Nonparametric Density Estimation）
1.概述
含义：
不假设数据服从某种分布，通过将样本空间划分为不同的区域并估计每个区域的概率来近似数据的概率密度函数。
原理：
对于高维空间中的一个随机向量x ，假设其服从一个未知分布p(x) ，则x落入空间中的小区域ℛ 的概率为:
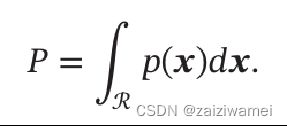
给定N个训练样本D= { x ( n ) } n = 1 N \{x^{(n)}\}_{n=1}^N {x(n)}n=1N,落入区域R的样本数量K服从二项分布:
当N 非常大时，我们可以近似认为:
假设区域R足够小，其内部的概率密度是相同的，则有:
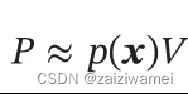
结合上述两个公式，得到
2. 直方图方法
一种非常直观的估计连续变量密度函数的方法，可以表示为一种柱状图。
3. 核密度估计（Kernel Density Estimation）
核密度估计是一种直方图方法的改进，也叫Parzen窗方法。
假设ℛ为d维空间中的一个以点x为中心的“超立方体”，并定义核函数来表示一个样本z是否落入该超立方体中
给定 个训练样本 = ( ) = 1 = {()}^_{=1} D=x(n)n=1N，落入区域ℛ 的样本数量 为
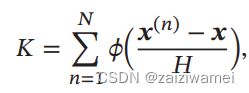
点 x 的密度估计为
4. K近邻方法
- 核密度估计方法中的核宽度是固定的，因此同一个宽度可能对高密度的区域过大，而对低密度区域过小。
- 一种更灵活的方式是设置一种可变宽度的区域，并使得落入每个区域中样本数量为固定的K。
- 要估计点x的密度，首先找到一个以x为中心的球体，使得落入球体的样本数量为K，就可以计算出点x的密度。
9.4 半监督学习
1. 自训练（Self-trainning）
2. 协同训练（Co-trainning）
