常见机器学习算法原理

1.线性回归

自变量与因变量是一种线性关系。
y=wx+b
y=w1x1+w2x2+……wnxn+w0x0
此处用w0x0代表b，w0=b，x0=1。
损失函数为1/2（yi-y^^）^2。即预测值与实际值之差的平方和最小。

预测值均值与实际值均值相等
一元线性回归的系数为：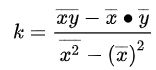
多元线性回归：

系数为：

2.逻辑回归

逻辑回归不是回归问题，它解决的是分类问题。
使用sigmoid函数可以让数据从负无穷到无穷变化为（0，1）

因此可以将其转化为概率
正例sigmoid(z)>0.5
负例sigmoid(z)<0.5

损失函数

p(y=1) = s(z)
p(y=0) = 1 - s(z)
综合两式可得
p（y）=s(z)^y * (1-s(z))^(1-y),然后取对数似然函数
由于是损失函数再取相反值，使其最小即可。

s(z)越大，y取1损失函数越小。
s(z)越小，y取0损失函数越小。

3. KNN

KNN即K邻近算法，预测一个样本使由其最近的K个邻居决定。
KNN用于分类，预测结果为K个邻居种类数量（或加权）最多的。
KNN用于回归，预测结果为K个邻居的均值（或加权均值）。

超参数是在训练模型前人为指定的参数，K值需要人为指定

K值大小	特性	模型
K值大	敏感性较低，稳定	容易欠拟合
K值小	敏感性较高，不稳定	容易过拟合

一般采用交叉验证（CV）的方式选择合适的K值
距离度量方式一般采用欧氏距离：

权重度量方式：
1.统一权重：所有样本权重相同
2.距离加权权重：样本的权重与待预测样本距离成反比

由于KNN是基于距离计算的，不同特征值的大小存在较大差异，例如身高一般在1.7m左右，而收入在几千至几万，如果直接计算距离收入的权重远大于身高。因此需要将不同特征的数据进行标准化。

常用的数据标准化方法有：

1. 均值标准差标准化（正态化）
2. 最大最小标准化

4.朴素贝叶斯

朴素贝叶斯假设每一个特征之间都是独立的。在特征间独立时效果很好。
它基于全概率公式和贝叶斯公式。
适用于垃圾邮件分类、新闻分类、情感分析等。
全概率公式

贝叶斯公式

sklearn中提供了不同的朴素贝叶斯算法，基于P（Xi|y）的分布假设使用不同的算法

朴素贝叶斯算法	特征类型	特征分布
高斯朴素贝叶斯	连续变量	正态分布
伯努利朴素贝叶斯	离散变量	二项分布
多项式朴素贝叶斯	离散变量	多项式分布

5.决策树

信息熵
信息熵用于描述信息的不确定度。不确定性越大，信息熵越大。

假设特征X有m个值，a1, a2……am，取a1的概率为p1。则信息熵计算公式如下：

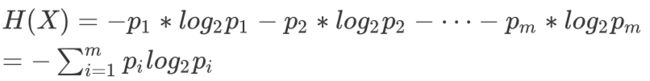
下图为二元信息熵与概率的分布。
取值概率约均匀时信息熵越大。
例如：一个班有10个男生，9个男生身高高于1.8m，1个低于1.8m
则随机抽一个男生，身高很大概率是1.8m，不确定度小，信息熵小
而当5个男生高于1.8m，5个男生低于1.8m时，
随机抽一个男生很难判断他的身高与1.8m的大小，即不确定度大，信息熵大。

决策树
sklearn决策树一般采用二叉树，可以处理分类和回归问题
分类问题：取子节点类别数量最多的类别作为结果
回归问题：取子节点的均值作为结果

分叉方式

每次基于一个特征进行分叉，原理都是基于使信息增益最大的方向进行特征选择。
信息增益为父节点的不纯度减去按权重分配的每个子节点的不纯度，即用该特征分叉后样本不纯度减少值最大。Np为父节点样本数，Nleft和Nright为左右节点样本数，I（D）为不纯度。

对于连续型特征，一般选择分类边界的均值A（可能有多个）计算信息增益后作为分界点，特征分叉取大于A或小于A。
对于离散性特征，则是分为属于或者不属于。

分裂停止条件

1. 所有子节点为同一类别
2. 数达到指定的最大深度
3. 叶子节点包含的数量小于指定值
4. 分裂后叶子节点的数量小于指定值
   不同算法的不纯度公式不同。

信息熵

基尼系数

决策树算法	不纯度	分叉方式	优缺点
ID3	信息熵	信息增益	多叉树、只支持分类，不支持连续特征、缺失值、选择特征时倾向于样本多的特征
C4.5	信息熵	信息增益率	多叉树，只支持分类，支持连续特征和缺失值，根据不同类别比值计算得到信息增益
CART	基尼系数	基尼增益	二叉树、支持分类和回归，支持连续特征和缺失值，回归时使MSE或MAE最小的特征分类

分类模型评估

分类模型一般有如下评估指标：

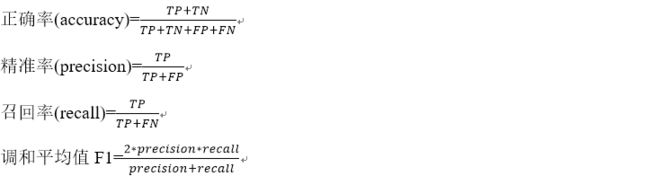
调和平均值的倒数=精准率的倒数和召回率的倒数的均值

ROC曲线

图形纵轴为TPR，横轴为FPR。设置不同的分类阈值会得到不同的FPR，TPR即图上的一个点，将这些点连接起来就可以得到ROC曲线。

一般用概率作为样本的分值。大于阈值的预测为正例，小于的预测为负例
当设置阈值大于1，则TP=0，FP=0，ROC过点（0，0）
当设置阈值小于0，则TN=0，FN=0，ROC过点（1，1）
完全随机时roc曲线为（0，0）到（1，1）的直线

AUC为ROC曲线下的面积，当TP增长较快时ROC曲线向上auc较大。反之较小。
auc的值越大表示模型的分类效果越好。

6. K-Means

K-Means是无监督学习（训练数据无样本标签，只有训练集没有测试集）。
聚类的目的是根据数据内部的特征，将数据划分为若干个类（簇）。使得同类之间相似度较高，不同类相似度较低。
K-Means即K均值算法，它会将数据分为K个簇。每个簇所有样本的均值叫“质心”。步骤如下：

1. 从样本中选K个点作为初始质心
2. 计算样本到质心的距离，将样本划分到距离最近的质心所在的簇中
3. 重新计算每个簇的均值（质心）
4. 重复步骤2，3直至达到最大迭代次数或质心移动位置小于指定阈值。

K-Means的预测即为样本距离哪个质心近，就预测为那个类别。
一般使用组内误差平方和SSE作为目标函数

K-Means的优点：
理解与实现容易;
易于扩展到大样本中；
应用范围很广

K-Means的缺点：
需要预先设置超参数K，K值不当模型效果会不好
受初始质心的影响
只适用于凸形的数据，对其他形状分布或不规则的数据效果较差。

K-Means的实现方法：
1.一次性训练所有的数据；
2.第一次训练一部分数据获得质心，然后每次增加一定量的数据，再更新质心。这么做可以有效的减少计算量，效果略小于一次性对全部样本训练；

为了克服初始质心的影响有如下解决方式：
1.随机n次质心，取SSE最小的那一组质心（当K值很大时，效果会变差）
2.采用K-Means++，其初始质心的选择方式与K-Means不同。
K-Means++选择质心的方法：

1. 随机选择一个样本作为质心。
2. 计算每一个非质心样本到现有最近质心的距离D(xi)
3. 根据概率
   选择下一个质心，m为非质心的样本数
4. 重复步骤2，3直至质心数目为K。

选择K值的方式
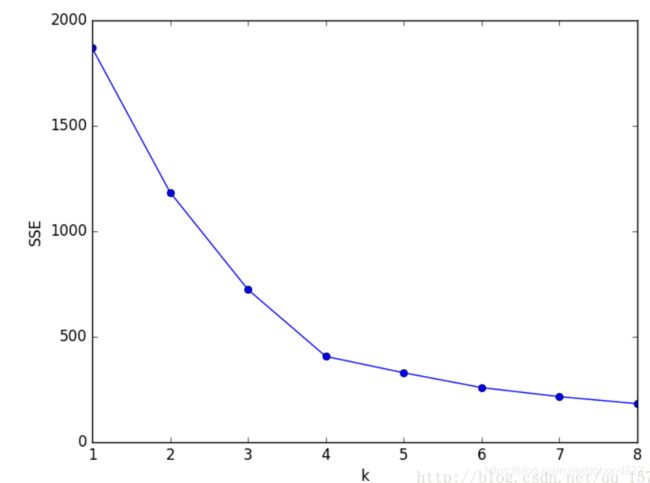
一般采用手肘法。当K值小于真实值时K值增大SSE应当明显降低，当超过真实值后SSE下降速度会很慢。SSE于K值的图形类似手肘，因此叫手肘法
根据图形选取，下图一般选K=4。