KDD 2016 | node2vec：Scalable Feature Learning for Networks

前言

题目：node2vec：网络的可拓展特征学习
会议：KDD2016
论文地址：node2vec: Scalable Feature Learning for Networks

本文将解读斯坦福大学的Aditya Grover和Jure Leskovec在KDD2016上发表的论文《Scalable Feature Learning for Networks》。该论文提出了一种高效的网络的可拓展特征学习方法–node2vec。本篇论文是北邮计算机学院大数据组2021年夏令营的考核论文，考核方式为：面试前一天告知论文名称，一天准备时间，面试中考察基本理论和实验。

本文实验很多，所以全文略长。

Abstract

网络中节点和边的预测任务都需要一个好的特征工程工作。 目前的特征学习方法不足以表达网络中观察到的连接模式的多样性。

因此，本文提出了node2vec方法：一种用于学习网络中节点的连续特征表示的算法框架。在node2vec 中，可以学习到节点到低维特征空间的映射，以最大化保留节点网络邻域的可能性。

node2vec的核心在于定义了一个节点网络邻域的灵活概念，并设计了一个有偏差的随机游走过程，这有效地探索了不同的邻域。

1.Introduction

网络分析中许多重要的任务都涉及到了对节点和边的预测。

在一个节点分类任务中，我们可以预测该网络中某个节点最有可能的标签。比如在社交网络中，我们可以预测某个用户可能感兴趣的对象；又或者在蛋白质-蛋白质网络中，我们可以预测蛋白质的功能标签。

如果是链接（边）预测，我们可以预测网络中两个节点是否应该相连。比如社交网络中预测两个用户是否是朋友关系。

显然，任何有监督的机器学习算法都需要一组特征。在网络预测问题中，这意味着我们需要为节点和边构造一个特征向量表示。 典型的方法是基于专家知识来手动构造，但显然这是没法在不同的预测任务中推广的。

另一种方法是通过解决一个优化问题来实现特征表示。然而，目前的技术无法很好地定义和优化一个合理的目标来实现网络中可伸缩的无监督特征学习。

经典方法如线性和非线性降维技术，有很大局限性：

• 如主成分分析、多维扩展等都涉及到矩阵的特征分解，这在现实生活中的大数据来说，计算代价很大。
• 此外，采用传统方法学到的特征在具体任务中的表现也比较差。

PCA的数学过程可以参考：降维基础知识（样本均值、样本方差、中心矩阵）与PCA（最大投影方差，最小重构代价，SVD分解）

除了传统的方法，我们还可以设计一个优化目标，以寻求保存节点的局部邻域，该目标可以通过SGD来进行优化。但这种方式依赖于一个严格的网络邻域概念，这导致这些方法在很大程度上对网络特有的连接模式不敏感。具体来说，网络中的节点可以根据其所属的社区进行组织(即同质性)；在其他情况下，可以基于网络中节点的结构角色进行组织。

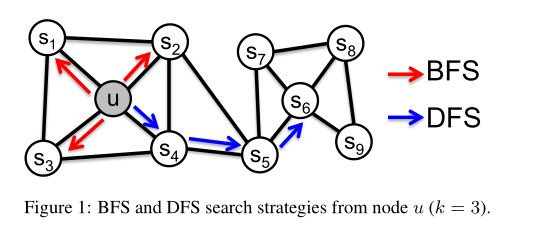
比如在图1中：节点$u$和$s_1$属于同一个紧密结合的节点社区，而节点$u$和$s_6$在两个不同的社区中都扮演着中枢节点的角色。

Present work

本文的主要贡献是定义了一个灵活的节点网络邻域概念。通过一个有偏随机游走来有效地探索给定节点的不同社区，然后返回一个游走序列。

算法是灵活的，可以通过可调参数控制搜索空间，而不是像之前的方法那样死板。

搜索什么？我们需要学到一个节点的特征向量表示，在此之前，我们首先要找到该节点的邻域节点，这些节点可以通过某种方法来生成，而这也是本文的重点。

有了节点的特征表示后，通过将两个节点的特征表示进行某种组合，就能这对节点的特征表示，也就是边的特征表示，进而就能进行边的预测。

本文的实验部分主要进行了在网络中两个比较常见的预测任务：

• 多标签分类任务：预测某个节点的标签
• 链接预测任务：预测两个节点间是否存在边。

总结本文贡献：

1. 提出了一种高效的网络的可拓展特征学习方法：node2vec。
2. 展示了node2vec如何符合现有网络预测中已有的原则，但同时又有灵活性在里面。
3. 扩展了node2vec和其他基于邻域的特征学习方法，从节点到节点对，用于基于边的预测任务。
4. 对node2vec在多个真实数据集上的多标签分类和链接预测进行了评估。

2.Related Work

这一节简单回顾了网络特征学习的相关工作。

无监督特征学习方法通常利用图的各种矩阵表示的性质，特别是拉普拉斯矩阵和邻接矩阵来进行特征学习。这点有在前文中提到，计算代价很大，并且效果也不是很好。

nlp中表示学习的最新进展为词汇等离散对象的特征学习开辟了新途径。Skip-gram模型旨在通过优化邻域保持似然目标来学习单词的连续特征表示。

skip-gram可以参考：论文阅读：Efficient Estimation of Word Representations in Vector Space

对于基于节点和基于边的预测任务，最近也有很多新的工作，这些体系结构使用多层非线性转换直接最小化下游预测任务的损失函数，从而获得较高的精度，但由于训练时间要求高，可扩展性不强。

于是必须提出一种新的方法！！

3.Feature Learning Framework

这部分介绍node2vec的细节。

将网络中的特征学习定义为一个最大似然优化问题。$G=(V,E)$表示网络。$f:V\to R^d$表示节点到其特征表示的映射函数，$d$是特征表示的维度，$f$是一个大小为$|V|\times d$的矩阵，$|V|$是节点个数，也就是说每个节点的特征表示都是一个$d$维的向量。

对每一个节点$u$，定义$N_s(u)$是通过邻域抽样策略$S$生成的节点$u$的网络邻域，$N_s(u)$是原始图中结点集$V$的子集。

将nlp中的skim-gram架构扩展到网络学习中：优化以下目标函数（使一个节点u根据其特征表示($f$)观察到网络邻域$N_s(u)$的对数概率最大化）

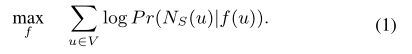
$P_r(N_s(u)|f(u))$表示根据一个节点的特征表示来观察其邻域的对数概率。最大化该概率的意义是什么？个人理解：经过$f$的映射后可以很好地保持各个节点间的邻居概念。

为了使上述优化问题易于处理，作者给出了两点假设：

1. 有条件的独立。我们通过假设观察一个邻域节点的可能性与观察任何其他邻域节点的可能性是独立的：
   
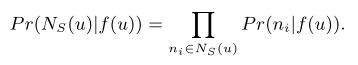
   很好理解！
2. 特征空间的对称性。源节点和邻域节点在特征空间中具有对称效应。据此，我们将每个源-邻域节点对的条件似然建模为softmax单元:
   

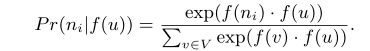
在上述两个假设下，公式1中的优化问题可以简化为：

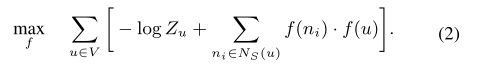
其中$Z_u$的表达式如下所示：
$$Z_u=\sum _{v\in V}exp(f(u)\cdot f(v))$$

对于大型网络，每个节点的$Z_u$的计算代价很高，因此使用负采样来近似它。

那怎么得到$N_s(u)$呢？下面将一一介绍！

3.1 Classic search strategies

对节点的邻域进行采样的经典策略主要包括两种：BFS和DFS，如下所示：

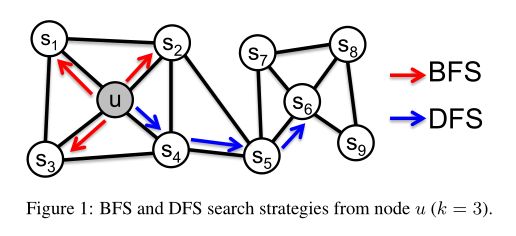
给定一个源节点$u$，我们的任务是找到它的邻域节点集合$N_s(u)$，假设我们需要采样$k$个节点。

• BFS：只能采样与$u$相邻的节点，例如上图中要寻找节点$u$的大小为3的邻域集合，则可以选择$s_1,s_2,s_3$三个节点。
• DFS：按照距离源节点距离依次增加的顺序进行采样，比如说对于节点$u$可以选择$s_4,s_5,s_6$三个节点。

根据同质性假设，属于相似网络集群的高度互联节点应该嵌入到一起，比如上图中的$u$和$s_1$，它们就属于同一网络集群。

而根据结构等价假设，在网络中具有相似结构角色的节点应该嵌入到一起，比如上图中的$u$和$s_6$，虽然属于不同网络集群，但是它们都是相应集群的中枢节点，角色类似。

结构等价不同于同质性，它不强调节点间必须互连，它们可能距离很远，这一点很重要。

BFS仅限于与源节点相连的节点，倾向于在初始节点的周围游走，可以反映出一个节点的邻居的微观特性。

而DFS（可以重复访问）一般会跑得离源节点越来越远，可以反映出一个节点邻居的宏观特性。

两种方法的局限都很明显：BFS只能探索图的很小一部分，而DFS移动到更大的深度会导致复杂的依赖关系，因为采样节点可能远离源，并且可能不太具有代表性。

3.2 node2vec

DFS和BFS都有各自的优缺点，于是本文提出了node2vec。下面介绍node2vec的细节。

3.2.1 Random Walks

给定一个源节点$u$，我们需要获得一个采样序列，序列长度为$l$。节点由以下分布生成：

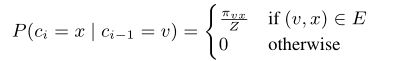
其中$c_i$表示第$i$个采样的节点。可以看出，第$i$个采样的节点与第$i-1$个采样的节点有着密切关系。${\pi }_{vx}$表示两个节点间的非归一化转移概率，$Z$是归一化常数。

简单解释下上述分布： 当第$i$个节点是$v$时（初始为$u$），我们采样下一个节点时，先找出所有与$v$相连的结点，然后算出$v$与这些结点间的非归一化转移概率，随后再进行采样。

3.2.2 Search bias $\alpha$

上图中，对于一个随机游走，如果已经采样了$(t,v)$ ，也就是说现在停留在节点$v$上，那么下一个要采样的节点$x$是哪个？作者定义了一个概率分布，也就是一个节点到它的不同邻居的转移概率：

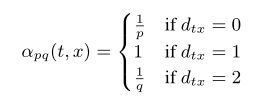
简单解释一下：

• 如果$t$与$x$相等，那么$x$被采样的概率是$1/p$
• 如果$t$与$x$相邻，那么$x$被采样的概率是1
• 如果$t$与$x$距离为2，那么$x$被采样的概率是$1/q$

要注意这里$t$已经被采样了！！

本文提出了返回参数$p$和出入参数$q$：参数用于控制随机游走产生的方式。需要说明的是，距离取值只能为$0,1,2$。

其中返回参数$p>max(q,1)$（第二种或者第三种情况），选取下一个点时会尽量不往回走；如果$p<min(q,1)$（更倾向于第一种情况）会倾向于围绕某节点打转。

出入参数q>1会倾向于在初始节点周围节点之间跑，反映出BFS特性，如果q比较小会往远处跑，表现出DFS特性。

3.2.3 The node2vec algorithm

看一下算法的参数：图$G$、节点特征向量的维度$d$、每个节点生成的游走个数$r$，游走长度$l$，上下文的窗口长度$k$，以及之前提到的$p、q$参数。

首先根据$p、q$和之前的公式计算一个节点到它的邻居的转移概率，此时形成了新的图$G^{{}^{\prime }}$。

1. walks用来存储随机游走，先初始化为空
2. 一共要进行$r$次循环，每一次循环要为图中每个节点都生成一个长度为$l$的游走序列
3. 第$r$次循环中对所有节点都利用node2vec算法生成一个随机游走walk，然后将其加入walks
4. 得到所有节点的$r$个游走序列后，根据上下文和该节点的游走序列利用SGD方法得到每一个节点的向量表示。

具体的node2vec算法：为某一个节点$u$生成一个游走序列。描述如下：

1. 将初始节点$u$加入到walk中
2. 当前节点curr为walk中最后一个节点
3. 根据curr和其对周围节点的转移概率选择下一个节点$s$，并加入walk
4. 当walk长度为$l$时采集结束

3.3 Learning edge features

node2vec算法可以得到网络中节点的特征向量表示。为了进行链路预测，也就是判断两个节点之间是否相连，我们需要将节点对表示成一个特征向量。具体做法就是在两个节点特征向量的基础上构造一个二元算子，比如平均，相加或者相减：

其中$f(u)$和$f(v)$表示两个节点的特征向量表示。经过上述运算后，就能得到节点对$(u,v)$的特征向量表示。注意$u$和$v$间可以不存在边。

4.Experiments

4.1 Case Study: Les Misérables network

网络来自于小说《Les Misérables network》中的人物关系。该网络有77个节点和254条边，令$d=16$，即我们需要给每个节点找到一个长度为16的特征向量表示。

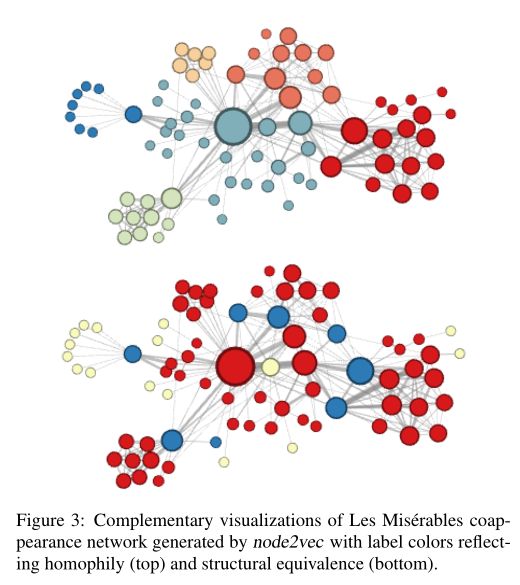
图3中顶部那副图对应$p=1,q=0.5$的情况。即$p=1,q=0.5$时算出每个节点的特征表示，然后根据特征表示进行聚类。在这个设置下，node2vec发现了小说中经常互动的角色集群。

为了发现哪些节点具有相同的结构角色，使用相同的网络，设置$p=1,q=2$，使用node2vec获取节点特征，然后根据获得的特征对节点进行聚类，结果如图3底部所示。蓝色节点代表了小说中不同次要情节之间的桥梁，他们具有相似的结构角色。

4.2 Experimental setup

通过与下面三个特征学习算法对比来评估node2vec的性能:

• 谱聚类：一种矩阵分解方法，我们将图G的归一化拉普拉斯矩阵的前d个特征向量作为节点的特征向量表示。
• Deepwalk：通过模拟均匀随机游动来学习特征表示，即node2vec中$p=1,q=1$的情况
• Line：在两个独立的阶段学习d维特征表示。第一阶段：通过类似于bfs的方法学习d/2维度。在第二阶段，通过严格地采样距离源节点2跳的节点来学习下一个d/2维。

node2vec的参数设置与DeepWalk和Line的典型值一致：$d=128,r=10,l=80,k=10$。

4.3 Multi-label classification

在多标签分类设置中，每个节点被分配一个或更多的标签，任务是预测节点的标签。

有以下三个数据集：

• BlogCatalog：BlogCatalog网站上列出的博客的社会关系网络。标签表示通过博主提供的元数据推断出的博主兴趣。该网络有10312个节点、333983条边和39个不同的标签。
• Protein-Protein Interactions (PPI)：蛋白质关系预测。该网络有3890个节点、76584条边和50个不同的标签。
• Wikipedia：一个词汇共现网络，出现在Wikipedia转储的前一百万字节中。这些标签代表了使用Stanford POS- tagger推断出来的词性(POS)标签。该网络共有4777个节点、184812条边和40种不同的标签。

节点特征表示被输入到一个L2正则化的一对一逻辑回归分类器，进而完成分类任务。

实验结果：

表2使用Macro-F1分数来衡量性能。可以看出，node2vec在三个网络的多标签分类中都取得了最好的结果。

上图给出了三个网络中各个模型在不同数据分割情况下的效果：横轴表示标记数据的比例，即测试集的比例。

可以发现：

1. 光谱聚类在三个网络中都是表现最差的。
2. DeepWalk要优于LINE。
3. node2vecs优于LINE和DeepWalk，且改进较大。

4.4 Parameter sensitivity

在图5a上图中，使用50%分割（测试集占一半）来检查参数pq的不同选择如何影响BlogCatalog数据集上的性能。可以发现：node2vec的性能随着出入参数p和返回参数q的减少而提高。 性能的提高可以基于我们期望在BlogCatalog中看到的同质性和结构等效性。

图5a下图这幅图显示了其它参数对性能的影响，即上文提到的$r,l,k$等。可以发现：增加它们都能提升性能，但会有饱和！

4.5 Perturbation Analysis

对于许多真实的网络，我们无法获得关于网络结构的准确信息。于是本文分析了node2vec对于两种与BlogCatalog网络中的边缘结构相关的不完全信息场景的性能。结果如图5b所示：

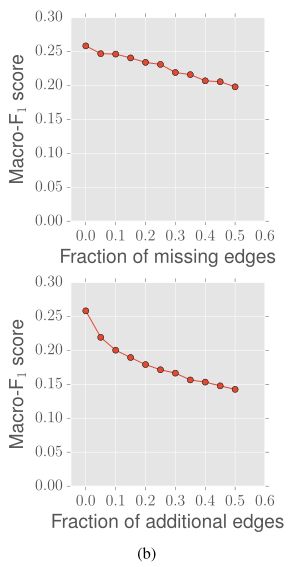
图5b上图显示了随着缺失边数的增加node2vec的性能，可以看到随着数据集中缺失边越来越多，性能是越来越差的，但是总体来说下降斜率比较平缓。

图5b下图显示了随着噪声边的增加node2vec的性能，可以看出噪声越多，性能越差，但其下降速率在不断变慢。

4.6 Scalability

为了测试可扩展性，做了如下实验：

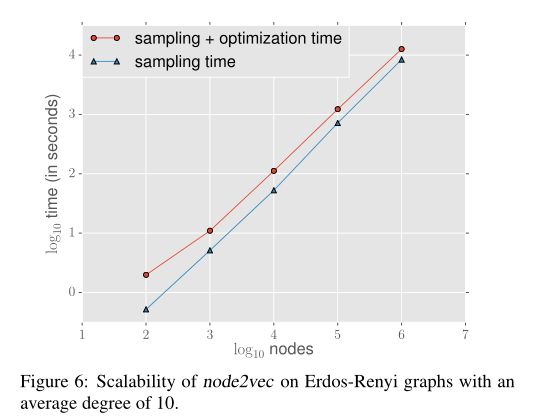
将图的节点从100个增加到1000000个，node2vec的时间复杂度在线性增加。

4.7 Link prediction

在链接预测中，网络去掉了一定比例的边，而我们需要预测这些缺失的边。

之前学术界关于链接预测的方案主要可以分为三类：启发式方法（Heuristic Methods），Network Embedding的方法和图神经网络方法。

1. 启发式方法（Heuristic Methods）： 主要考虑利用两个节点之间一些预先定义的特征来衡量节点之间的相似度，比如，节点的共同邻居（Common Neighbor），Jaccard相似度，Katz Index等，这样的方法假设存在边关系的节点之间存在某种特定的结构特性，但这样的假设不一定对任意网络都有效。
2. Network Embeddings方法： 使用基于游走的方法得到经过某个节点的多条路径，再通过Skip-Gram和CBOW的方式，对路径上mask的节点进行预测。这样的方法，没有直接将链接预测任务嵌入到有监督学习的流程中，并且无法较好的利用用户的节点属性，无法达到较好的预测精度。
3. 图神经网络（graph neural network，GNN）： 主要分为两类，节点为中心的图神经网络模型（Node-centric GNN）和边为中心的图神经网络模型（Edge-centric GNN）。

数据集：

• Facebook：在Facebook网络中，节点代表用户，边代表任意两个用户之间的朋友关系。该网络有4039个节点和88234条边。
• Protein-Protein Interactions (PPI)：在智人的蛋白质相互作用网络中，节点代表蛋白质，边代表一对蛋白质之间的生物相互作用。该网络有19706个节点和390633条边。
• arXiv ASTRO-PH：一个合作网络，其中的节点代表科学家，如果两位科学家合作写过一篇论文，那么他们之间就会有一条边。该网络有18722个节点和198110条边。

实验结果如下表所示：

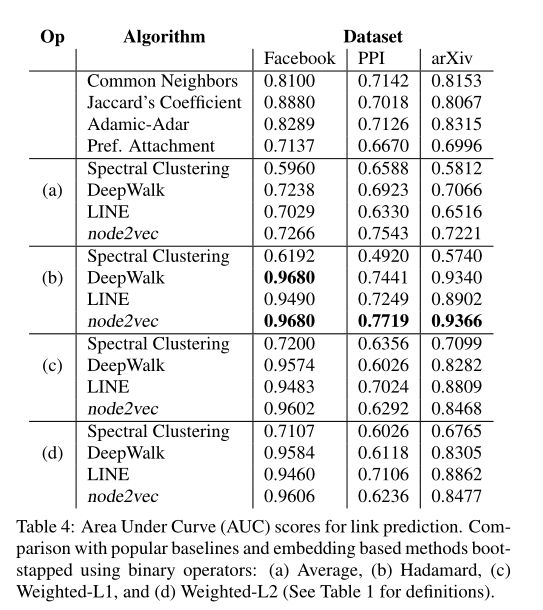
分析：最上边的一部分为启发式方法的预测效果，作为基准。

1. node2vec在arXiv数据集上取得了最好效果，相比于启发式方法中最好的Adamic-Adar提高了12.6%。
2. node2vec在所有网络中都优于DeepWalk和LINE。
3. 除了Weighted-L1和Weighted-L2（见表1）运算符外，node2vec的表现优于DeepWalk和LINE
4. Hadamard运算符与node2vec一起使用时性能最佳(b)。
   

5.Discussion and Conclusion

原文中本部分叙述较多，大致总结一下：

1. BFS仅限于与源节点相连的节点，倾向于在初始节点的周围游走，可以反映出一个节点的邻居的微观特性。
2. DFS一般会跑的离初始节点越来越远，可以反映出一个节点邻居的宏观特性。
3. BFS只能探索网络的很小一部分，而DFS虽然可以移动到更大的深度，但由于采样节点远离源，可能会导致复杂的依赖关系，并且可能不太具有代表性。
4. DeepWalk和LINE可以被视为一种比较严格的搜索策略。DeepWalk采用均匀随机游走($p=1,q=1$)进行搜索，它不能让我们控制已探索的集群。LINE在探索更深层次的节点时，它是有局限性的，并且没有灵活性。
5. 相比之下，node2vec搜索策略是灵活和可控的，并且取得了更好的实验效果。此外，从实际的角度来看，node2vec是可扩展的，并且具有很强的鲁棒性。