空间机器人建模与仿真报告
大作业做空间悬浮机器人模拟仿真,发现网上没有相关的资料,于是就做了个,现在发出来给需要的人用吧
下载连接:https://download.csdn.net/download/tiandajiang/85064569
目录
(1)空间两杆机器人建模
(2)空间悬浮机器人运动学模型
(3)空间悬浮机器人动力学模型
(4)动力学空间轨迹规划
规划过程介绍
固定位姿动力学轨迹规划
固定位置动力学轨迹规划
固定姿态动力学轨迹规划
悬浮状态动力学轨迹规划
(4)总结
附1:空间机器人simulink仿真模型图
附2:轨迹规划算法
附3:动力学奇异
(1)空间两杆机器人建模
建立空间两杆机器人模型,设置机器人参数,构建机器人坐标系,并完成模型导入simulink。
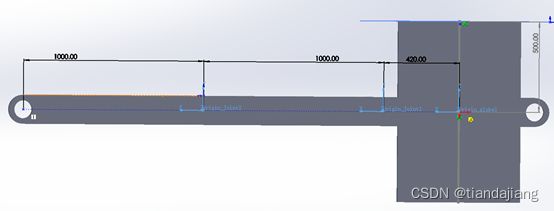
图 1 空间两杆机器人简图
杆件长度参数表为:
| 杆长参数(m) | ||||
|---|---|---|---|---|
| r0 | l1 | r1 | l2 | r2 |
| 0.42 | 0.5 | 0.5 | 0.5 | 0.5 |
基座杆件质量参数表为:
| 质量参数(kg) | |||
|---|---|---|---|
| M | m0 | m1 | m2 |
| 50 | 40 | 5 | 5 |
基座杆件惯量参数为:
| 惯量参数 | ||
|---|---|---|
| I0 | I1 | I2 |
| 4.4 | 0.94 | 0.94 |
最终获得solidworks空间两杆机器人仿真模型为:
图 2 空间两杆机器人模型
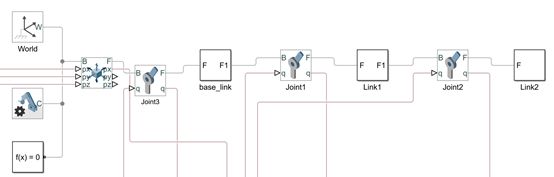
在solidworks中绘制机械臂的简单模型,需要将零件文件导入simulink中,完成坐标系变换的设置,并完成机械臂的搭建,此处惯性坐标系与模型体坐标系通过两个关节连接,一个全向移动关节和转动关节模拟悬浮空间。
图 3 simulink空间机器人模型
最终得到的空间悬浮机器人效果图如下
图 4 simulink 空间机器人效果图
(2)空间悬浮机器人运动学模型
对空间悬浮机器人进行控制和轨迹规划,必须获取空间机器人末端位置姿态,末端及各关节点速度,因此需要建立悬浮机器人运动学模型。
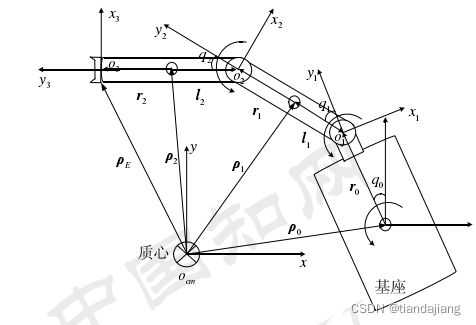
这里涉及转换的坐标系有:惯性坐标系,基座质心坐标系,关节坐标系,杆件质心坐标系。其坐标系示意图如下所示:
图 5 空间悬浮机器人示意图
涉及转换过程中为了计算及建模方便,我们并没有使用机器人质心作为惯性坐标系原点,而是将初始时刻基座质心作为惯性坐标系原点进行坐标系转换,计算过程中还进行了一定简化,即r2=l2,r1=l1,以后的计算均使用r表示。
将转换矩阵进行matlab进行matlab编程,即可获得末端位置相对于基座的位置:
使用[RJ,RL,rJ,rL,e,g]=Kinematics(R0,r0,qm,robot)获取所需的位置关系
末端速度需要对求解运动学微分,其表达式为:
可以通过[Bij,Bi0,P0,pm]=DiffKinematics
(R0,r0,rL,e,g,robot)获取各连杆之间的转换矩阵。
雅克比矩阵[J0n,Jmn]=Jacob(rL(1:3,end),r0,rL,P0,pm,2,robot)得到,末端速度可表示为:

Matlab编程中使用的函数功能:
-
[RJ,RL,rJ,rL,e,g]=Kinematics(R0,r0,qm,robot) 运动学
其中R0,r0表示基座相对于惯性系的旋转矩阵和位置矩阵qm表示关节角转动情况。
RJ,rJ表示关节相对于惯性坐标系的旋转矩阵和位置矩阵
RL,rL表示连杆质心相对于惯性坐标系的旋转矩阵和位置矩阵
e,g分别表示关节角旋转轴和关节相对上一关节位置
-
[Bij,Bi0,P0,pm]=DiffKinematics(R0,r0,rL,e,g,robot) 运动学微分
R0,r0,rL,e,g解释见上一函数
Bij第i个连杆相对于第j连杆的转动传递矩阵,
Bi0第i个连杆相对于基座的转动传递矩阵
P0基座向外传递的转动速度
Pm各关节向外传递的转动速度
-
[J0n,Jmn]=Jacob(rL(1:3,end),r0,rL,P0,pm,2,robot) 速度求解
参数及输出文中均有所介绍
末端运动学模型均建立在惯性坐标系的基础上,但运动学在悬浮空间无法求得唯一位置解,还需要运动学求解其在关系坐标系的位置姿态。
(3)空间悬浮机器人动力学模型
动力学模型的建立可以求得悬浮机器人在悬浮状态时基座在惯性坐标系中位置姿态的相对变化量,动力学模型是一组微分方程,对其进行积分可以确定基座某一时刻的位置姿态。
首先获取基座连杆转动惯量[I0,Im]=I_I(R0,RL,robot),进而获得惯性矩阵和哥氏惯性力矩阵。其计算过程可通过matlab函数功能实现。
[H0, H0m, Hm] = GIM(M0_tilde,Mm_tilde,Bij,Bi0,P0,pm,robot)
[C0,C0m,Cm0,Cm]=CIM(t0,tm,I0,Im,M0_tilde,Mm_tilde,Bij,Bi0,P0,pm,robot)
逆动力学,在之后的规划设计中,悬浮状态需要获得基座的速度和转动角速度,在求解过程中,将关节转动角速度作为输入,求得基座的速度和转动角速度,关于动力学模型的进一步推导,由于之后的计算没有用到,所以不进行。
Matlab编程中使用的函数功能:
-
[H0, H0m, Hm] = GIM(M0_tilde,Mm_tilde,Bij,Bi0,P0,pm,robot)
相关参数上文均介绍
-
[C0,C0m,Cm0,Cm]=CIM(t0,tm,I0,Im,M0_tilde,Mm_tilde,Bij,Bi0,P0,pm,robot)
相关参数上文均介绍
(4)动力学空间轨迹规划
轨迹规划过程是一个迭代更新过程,由于当前并没有一个成熟的可视化悬浮机器人仿真模型,因此在计算过程中只能使用已建立的运动学和动力学模型进行模型的运动状态求解,空间悬浮机器人在悬浮状态工作时,我们并不能直接计算任意时刻机器人的位置姿态,因此只能在得知当前位置姿态后更新下一步所需要施加的关节运动状态。
规划过程介绍
轨迹规划过程可分为逼近过程和减速过程,我们在设计逼近过程时由于精度要求所以将逼近过程分为牛顿迭代法和速度向量匹配两步进行。
牛顿迭代法:在大范围内逼近目标坐标,具体实现是采用位置梯度下降最快的方向进行机器人的操控,因此即使机器人出现动力学奇异现象也不会导致机器人卡死,但由于梯度下降在位置差矢量很小时难以操控,会导致末端位置绕目标旋转,难以保证精度,在计算过程中牛顿迭代法精度只能达到0.1m,其matlab实现代码在附录可查看。
位置矢量匹配法:位置矢量匹配法是一种小范围逼近目标的方法,可以看作迭代法的变形,是将操作带来的末端变化预代入到动力学方程,以获取当前操作能够带来的位置增量,将位置增量的矢量方向作为输入,匹配其方向矢量指向,如果指向目标即完成匹配过程,当发生动力学奇异时,无法匹配得到正确的位置增量对应的操作,因此只能作为一种辅助方式在小范围内提高逼近精度,在规划过程中如果没有出现动力学奇异,可以将精度提高到0.01m以下。具体实现在附录中可查看。
减速过程:减速过程较容易理解,计算当前速度,施加相应的减速操作,即可在预定时间完成减速过程。
图 6 轨迹规划流程图
以下将进行空间悬浮机器人在不同工作状态下工作情况介绍。
固定位姿动力学轨迹规划
空间机器人工作在固定位姿模式时,基座位姿可以确定,因此通过运动学是可以确定空间机器人末端唯一位姿解,可以使用传统方法直接进行轨迹规划,这里只是验证动力学轨迹规划实现的可能。
固定位姿动力学轨迹规划过程主要考虑到达目标的响应,以及目标点跟踪的精度,我们规划的轨迹为50点轨迹,即使末端跟踪50个点,以此验证算法的可靠性。
使用固定位姿工作状态的轨迹规划为跟踪一条2次曲线,跟踪时间13.6s完成,响应时间比较快,跟踪误差均在0.01m范围内。以下是跟踪过程的相关参数曲线图:
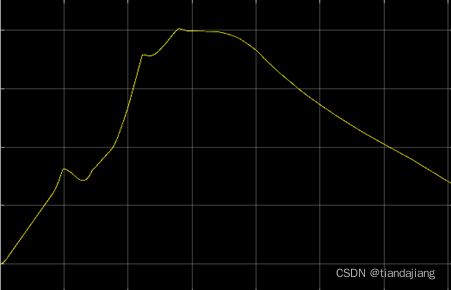
图 7 关节角q1角度变化曲线
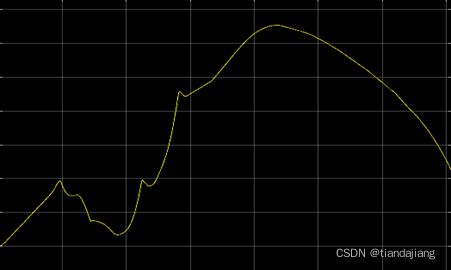
图 8 关节角q2角度变化曲线
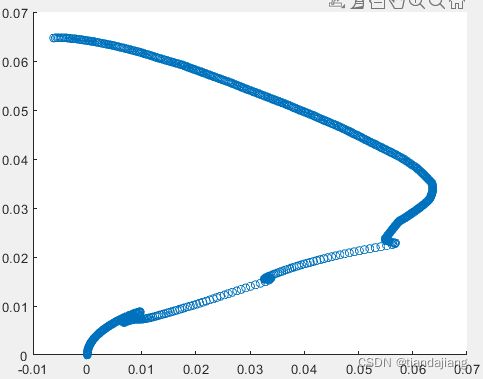
图 9 末端轨迹曲线
从末端轨迹规划曲线来看,算法对各点位跟踪达到了很好的效果,但也可以看出,某些位置出现绕目标旋转的轨迹,这是由于速度向量比配无法在小范围工作的结果,关节角变化较为平稳。
其相应的规划动画如下
固定位置动力学轨迹规划
空间机器人工作在固定位置模式时,基座位置可以确定,姿态变化,但可以通过运动学角动量守恒求得基座姿态,因此通过运动学是也是可以确定空间机器人末端唯一位姿解,使用传统方法直接进行轨迹规划是需要将基座旋转角度考虑进去,这里验证动力学轨迹规划实现的情况。
固定位置动力学轨迹规划过程设计了一次抛物线轨迹跟踪,规划的轨迹为50点轨迹,即使末端跟踪50个点,以此验证算法的可靠性。
使用固定位置工作状态的轨迹规划为跟踪一条抛物线,跟踪时间21s完成,响应时间比较快,跟踪误差均在0.01m范围内。以下是跟踪过程的相关参数曲线图:
图 10 关节角q1角度变化曲线
图 11 关节角q2角度变化曲线
图 12 关节角q0角度变化曲线
图 13 末端位置变化曲线
与固定位姿的规划相比,多了q0的角度变化,规划难道增加,但从末端轨迹规划曲线来看,算法对各点位跟踪达到了很好的效果,关节角变化也较为平稳。
其相应的规划动画如下
固定姿态动力学轨迹规划
空间机器人工作在固定姿态模式时,基座姿态可以确定,此时基座的位置在运动学方程中已存在无穷解,因此不能通过运动学确定空间机器人末端唯一位姿解,使用传统方法也无法进行轨迹规划,需要动力学轨迹规划,此外固定姿态也需要对动力学奇异进行考虑,动力学奇异的介绍见附录。
固定姿态动力学轨迹规划过程设计了一次三角函数轨迹跟踪,规划的轨迹为50点轨迹,即使末端跟踪50个点,以此验证算法的可靠性。
使用固定位置工作状态的轨迹规划时,跟踪时间20.25s完成,响应时间比较快,跟踪误差均在0.01m范围内。以下是跟踪过程的相关参数曲线图:
图 14 关节角q1角度变化
图 15 关节角q2角度变化
图 16 基座位置轨迹
图 17 末端位置变化曲线
与固定位姿的规划相比,多了基座位置变化,规划难道增加,其中多处出现绕点选择的情况,这可能是是在小范围内发生动力学奇异的现象,但从末端轨迹规划曲线来看,算法对各点位跟踪达到了很好的效果,关节角变化也较为平稳,基座位置变化也较为显著。
其相应的规划动画如下
悬浮状态动力学轨迹规划
空间机器人工作在悬浮模式时,基座位置姿态均位置,无法用运动学求解,不能使用传统方法进行轨迹规划,需要动力学轨迹规划,此外悬浮状态需要对动力学奇异进行考虑,动力学奇异的介绍见附录。
悬浮状态动力学轨迹规划过程设计了0.4m的圆形轨迹跟踪,规划的轨迹为50点轨迹,即使末端跟踪50个点,以此验证算法的可靠性。
使用悬浮状态工作模式的轨迹规划,跟踪时间24.4s完成,响应时间比较快,跟踪误差均在0.01m范围内。以下是跟踪过程的相关参数曲线图:
图 18 关节角q1角度变化曲线
图 19 关节角q2变化曲线
图 20 关节角q0变化曲线
图 21 基座位置变化
图 22 末端轨迹曲线
与固定位姿的规划相比,多了基座位置和姿态的变化,规划难道增加,虽然规划效果也不错,但其中多处出现绕点旋转的情况,这是在小范围内发生动力学奇异的现象,算法对各点位跟踪达到了很好的效果,关节角变化也较为平稳,基座位置变化也较为显著。
其相应的规划动画如下
(4)总结
遇到的难题:程序设计的过程,运动学推导过程,动力学奇异过程,由于牛顿迭代逼近法不受动力学奇异影响,所以在本规划中影响有限,但分析过程存在一定难点。
创新点:将路径规划逼近过程分为2部分进行,即牛顿迭代法和位置向量匹配法,提高了跟踪精度。





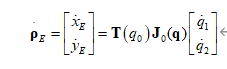
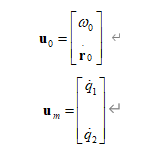



![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hdEli3qn-1642518318415)(media/7aef539b9c824829434ee3e2fef921ce.png)]](http://img.e-com-net.com/image/info8/070ca79821184875904484aaea46e6ea.jpg)